No-regret Exploration in Shuffle Private Reinforcement Learning

Differential privacy (DP) has recently been introduced into episodic reinforcement learning (RL) to formally address user privacy concerns in personalized services. Previous work mainly focuses on two trust models of DP: the central model, where a central agent is responsible for protecting users' sensitive data, and the (stronger) local model, where the protection occurs directly on the user side. However, they either require a trusted central agent or incur a significantly higher privacy cost, making it unsuitable for many scenarios. This work introduces a trust model stronger than the central model but with a lower privacy cost than the local model, leveraging the emerging \emph{shuffle} model of privacy. We present the first generic algorithm for episodic RL under the shuffle model, where a trusted shuffler randomly permutes a batch of users' data before sending it to the central agent. We then instantiate the algorithm using our proposed shuffle Privatizer, relying on a shuffle private binary summation mechanism. Our analysis shows that the algorithm achieves a near-optimal regret bound comparable to that of the centralized model and significantly outperforms the local model in terms of privacy cost.

Tractable Offline Learning of Regular Decision Processes

This work studies offline Reinforcement Learning (RL) in a class of non-Markovian environments called Regular Decision Processes (RDPs). In RDPs, the unknown dependency of future observations and rewards from the past interactions can be captured by some hidden finite-state automaton. For this reason, many RDP algorithms first reconstruct this unknown dependency using automata learning techniques. In this paper, we show that it is possible to overcome two strong limitations of previous offline RL algorithms for RDPs, notably RegORL. This can be accomplished via the introduction of two original techniques: the development of a new pseudometric based on formal languages, which removes a problematic dependency on $L_\infty^\mathsf{p}$-distinguishability parameters, and the adoption of Count-Min-Sketch (CMS), instead of naive counting. The former reduces the number of samples required in environments that are characterized by a low complexity in language-theoretic terms. The latter alleviates the memory requirements for long planning horizons. We derive the PAC sample complexity bounds associated to each of these techniques, and we validate the approach experimentally.

How to Shrink Confidence Sets for Many Equivalent Discrete Distributions?

We consider the situation when a learner faces a set of unknown discrete distributions $(p_k)_{k\in \mathcal K}$ defined over a common alphabet $\mathcal X$, and can build for each distribution $p_k$ an individual high-probability confidence set thanks to $n_k$ observations sampled from $p_k$. The set $(p_k)_{k\in \mathcal K}$ is structured: each distribution $p_k$ is obtained from the same common, but unknown, distribution q via applying an unknown permutation to $\mathcal X$. We call this \emph{permutation-equivalence}. The goal is to build refined confidence sets \emph{exploiting} this structural property. Like other popular notions of structure (Lipschitz smoothness, Linearity, etc.) permutation-equivalence naturally appears in machine learning problems, and to benefit from its potential gain calls for a specific approach. We present a strategy to effectively exploit permutation-equivalence, and provide a finite-time high-probability bound on the size of the refined confidence sets output by the strategy. Since a refinement is not possible for too few observations in general, under mild technical assumptions, our finite-time analysis establish when the number of observations $(n_k)_{k\in \mathcal K}$ are large enough so that the output confidence sets improve over initial individual sets. We carefully characterize this event and the corresponding improvement. Further, our result implies that the size of confidence sets shrink at asymptotic rates of $O(1/\sqrt{\sum_{k\in \mathcal K} n_k})$ and $O(1/\max_{k\in K} n_{k})$, respectively for elements inside and outside the support of q, when the size of each individual confidence set shrinks at respective rates of $O(1/\sqrt{n_k})$ and $O(1/n_k)$. We illustrate the practical benefit of exploiting permutation equivalence on a reinforcement learning task.

Improved Exploration in Factored Average-Reward MDPs

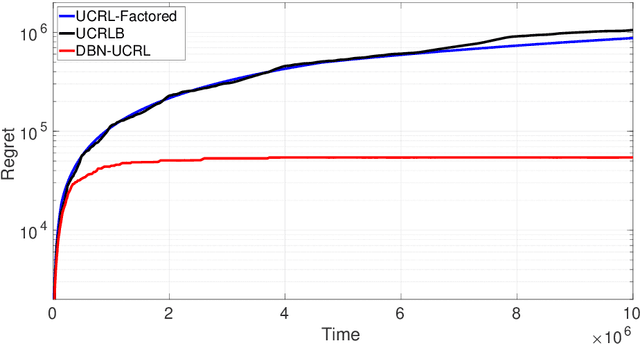
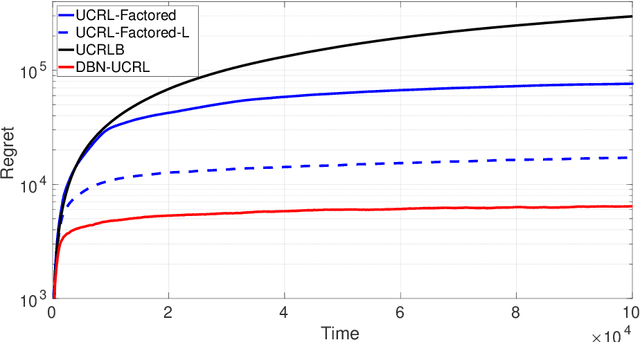
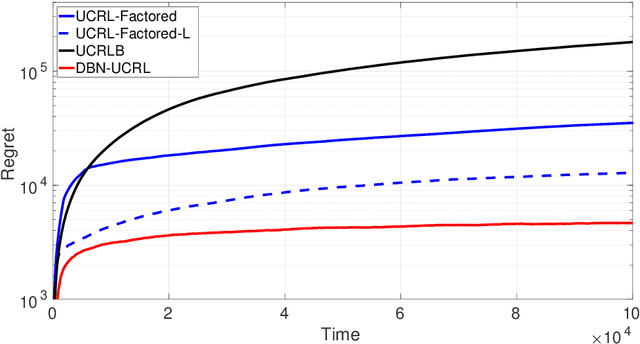
We consider a regret minimization task under the average-reward criterion in an unknown Factored Markov Decision Process (FMDP). More specifically, we consider an FMDP where the state-action space $\mathcal X$ and the state-space $\mathcal S$ admit the respective factored forms of $\mathcal X = \otimes_{i=1}^n \mathcal X_i$ and $\mathcal S=\otimes_{i=1}^m \mathcal S_i$, and the transition and reward functions are factored over $\mathcal X$ and $\mathcal S$. Assuming known factorization structure, we introduce a novel regret minimization strategy inspired by the popular UCRL2 strategy, called DBN-UCRL, which relies on Bernstein-type confidence sets defined for individual elements of the transition function. We show that for a generic factorization structure, DBN-UCRL achieves a regret bound, whose leading term strictly improves over existing regret bounds in terms of the dependencies on the size of $\mathcal S_i$'s and the involved diameter-related terms. We further show that when the factorization structure corresponds to the Cartesian product of some base MDPs, the regret of DBN-UCRL is upper bounded by the sum of regret of the base MDPs. We demonstrate, through numerical experiments on standard environments, that DBN-UCRL enjoys a substantially improved regret empirically over existing algorithms.

Tightening Exploration in Upper Confidence Reinforcement Learning

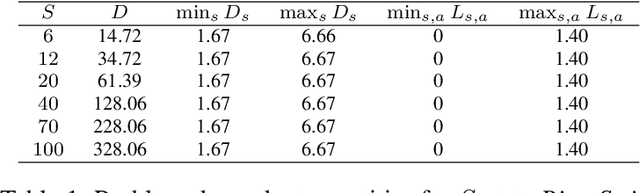
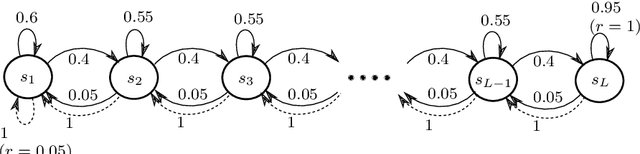
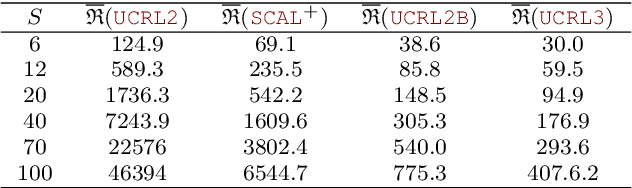
The upper confidence reinforcement learning (UCRL2) strategy introduced in (Jaksch et al., 2010) is a popular method to perform regret minimization in unknown discrete Markov Decision Processes under the average-reward criterion. Despite its nice and generic theoretical regret guarantees, this strategy and its variants have remained until now mostly theoretical as numerical experiments on simple environments exhibit long burn-in phases before the learning takes place. Motivated by practical efficiency, we present UCRL3, following the lines of UCRL2, but with two key modifications: First, it uses state-of-the-art time-uniform concentration inequalities, to compute confidence sets on the reward and transition distributions for each state-action pair. To further tighten exploration, we introduce an adaptive computation of the support of each transition distributions. This enables to revisit the extended value iteration procedure to optimize over distributions with reduced support by disregarding low probability transitions, while still ensuring near-optimism. We demonstrate, through numerical experiments on standard environments, that reducing exploration this way yields a substantial numerical improvement compared to UCRL2 and its variants. On the theoretical side, these key modifications enable to derive a regret bound for UCRL3 improving on UCRL2, that for the first time makes appear a notion of local diameter and effective support, thanks to variance-aware concentration bounds.

Model-Based Reinforcement Learning Exploiting State-Action Equivalence

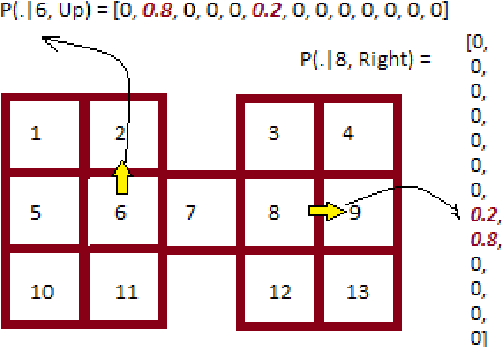
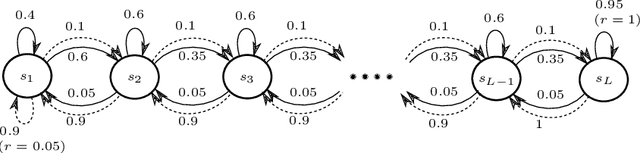
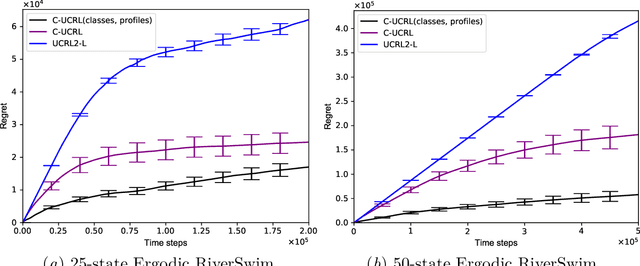
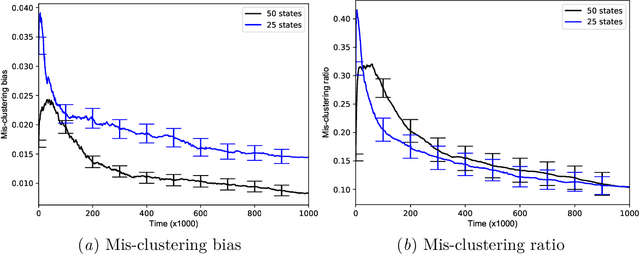
Leveraging an equivalence property in the state-space of a Markov Decision Process (MDP) has been investigated in several studies. This paper studies equivalence structure in the reinforcement learning (RL) setup, where transition distributions are no longer assumed to be known. We present a notion of similarity between transition probabilities of various state-action pairs of an MDP, which naturally defines an equivalence structure in the state-action space. We present equivalence-aware confidence sets for the case where the learner knows the underlying structure in advance. These sets are provably smaller than their corresponding equivalence-oblivious counterparts. In the more challenging case of an unknown equivalence structure, we present an algorithm called ApproxEquivalence that seeks to find an (approximate) equivalence structure, and define confidence sets using the approximate equivalence. To illustrate the efficacy of the presented confidence sets, we present C-UCRL, as a natural modification of UCRL2 for RL in undiscounted MDPs. In the case of a known equivalence structure, we show that C-UCRL improves over UCRL2 in terms of regret by a factor of $\sqrt{SA/C}$, in any communicating MDP with $S$ states, $A$ actions, and $C$ classes, which corresponds to a massive improvement when $C \ll SA$. To the best of our knowledge, this is the first work providing regret bounds for RL when an equivalence structure in the MDP is efficiently exploited. In the case of an unknown equivalence structure, we show through numerical experiments that C-UCRL combined with ApproxEquivalence outperforms UCRL2 in ergodic MDPs.

Variance-Aware Regret Bounds for Undiscounted Reinforcement Learning in MDPs

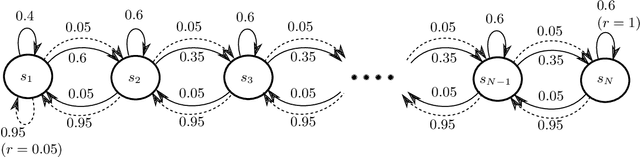
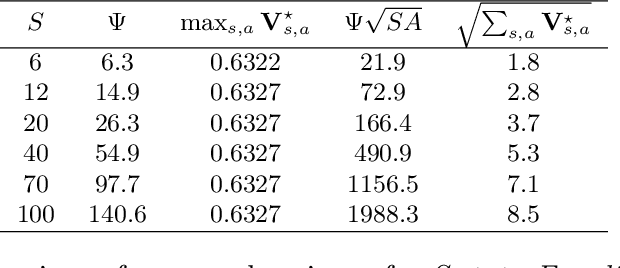
The problem of reinforcement learning in an unknown and discrete Markov Decision Process (MDP) under the average-reward criterion is considered, when the learner interacts with the system in a single stream of observations, starting from an initial state without any reset. We revisit the minimax lower bound for that problem by making appear the local variance of the bias function in place of the diameter of the MDP. Furthermore, we provide a novel analysis of the KL-UCRL algorithm establishing a high-probability regret bound scaling as $\widetilde {\mathcal O}\Bigl({\textstyle \sqrt{S\sum_{s,a}{\bf V}^\star_{s,a}T}}\Big)$ for this algorithm for ergodic MDPs, where $S$ denotes the number of states and where ${\bf V}^\star_{s,a}$ is the variance of the bias function with respect to the next-state distribution following action $a$ in state $s$. The resulting bound improves upon the best previously known regret bound $\widetilde {\mathcal O}(DS\sqrt{AT})$ for that algorithm, where $A$ and $D$ respectively denote the maximum number of actions (per state) and the diameter of MDP. We finally compare the leading terms of the two bounds in some benchmark MDPs indicating that the derived bound can provide an order of magnitude improvement in some cases. Our analysis leverages novel variations of the transportation lemma combined with Kullback-Leibler concentration inequalities, that we believe to be of independent interest.