Provably Efficient Exploration in Reward Machines with Low Regret

We study reinforcement learning (RL) for decision processes with non-Markovian reward, in which high-level knowledge of the task in the form of reward machines is available to the learner. We consider probabilistic reward machines with initially unknown dynamics, and investigate RL under the average-reward criterion, where the learning performance is assessed through the notion of regret. Our main algorithmic contribution is a model-based RL algorithm for decision processes involving probabilistic reward machines that is capable of exploiting the structure induced by such machines. We further derive high-probability and non-asymptotic bounds on its regret and demonstrate the gain in terms of regret over existing algorithms that could be applied, but obliviously to the structure. We also present a regret lower bound for the studied setting. To the best of our knowledge, the proposed algorithm constitutes the first attempt to tailor and analyze regret specifically for RL with probabilistic reward machines.

Tightening Exploration in Upper Confidence Reinforcement Learning

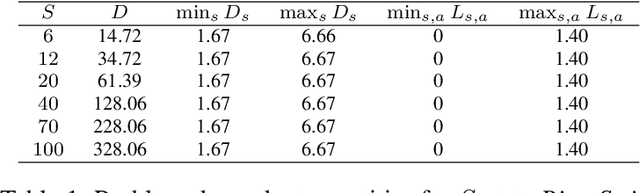
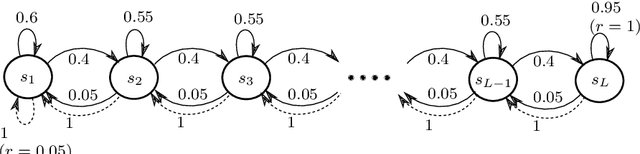
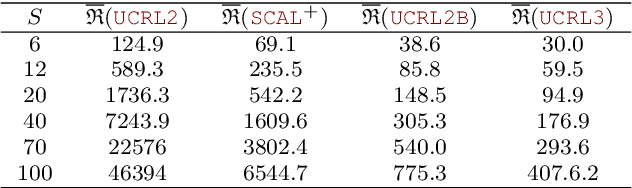
The upper confidence reinforcement learning (UCRL2) strategy introduced in (Jaksch et al., 2010) is a popular method to perform regret minimization in unknown discrete Markov Decision Processes under the average-reward criterion. Despite its nice and generic theoretical regret guarantees, this strategy and its variants have remained until now mostly theoretical as numerical experiments on simple environments exhibit long burn-in phases before the learning takes place. Motivated by practical efficiency, we present UCRL3, following the lines of UCRL2, but with two key modifications: First, it uses state-of-the-art time-uniform concentration inequalities, to compute confidence sets on the reward and transition distributions for each state-action pair. To further tighten exploration, we introduce an adaptive computation of the support of each transition distributions. This enables to revisit the extended value iteration procedure to optimize over distributions with reduced support by disregarding low probability transitions, while still ensuring near-optimism. We demonstrate, through numerical experiments on standard environments, that reducing exploration this way yields a substantial numerical improvement compared to UCRL2 and its variants. On the theoretical side, these key modifications enable to derive a regret bound for UCRL3 improving on UCRL2, that for the first time makes appear a notion of local diameter and effective support, thanks to variance-aware concentration bounds.

Model-Based Reinforcement Learning Exploiting State-Action Equivalence

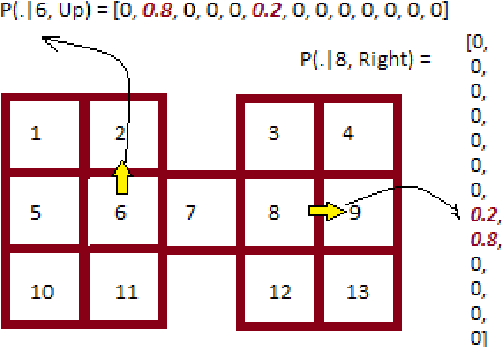
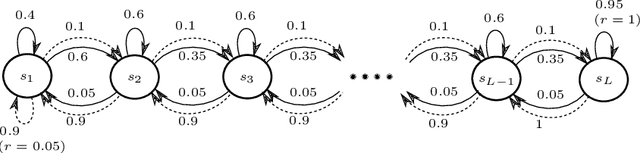
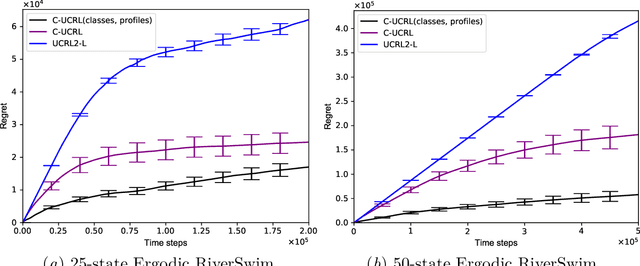
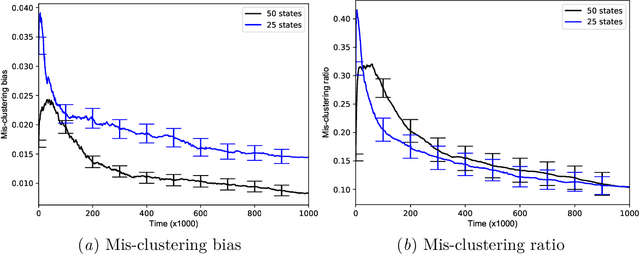
Leveraging an equivalence property in the state-space of a Markov Decision Process (MDP) has been investigated in several studies. This paper studies equivalence structure in the reinforcement learning (RL) setup, where transition distributions are no longer assumed to be known. We present a notion of similarity between transition probabilities of various state-action pairs of an MDP, which naturally defines an equivalence structure in the state-action space. We present equivalence-aware confidence sets for the case where the learner knows the underlying structure in advance. These sets are provably smaller than their corresponding equivalence-oblivious counterparts. In the more challenging case of an unknown equivalence structure, we present an algorithm called ApproxEquivalence that seeks to find an (approximate) equivalence structure, and define confidence sets using the approximate equivalence. To illustrate the efficacy of the presented confidence sets, we present C-UCRL, as a natural modification of UCRL2 for RL in undiscounted MDPs. In the case of a known equivalence structure, we show that C-UCRL improves over UCRL2 in terms of regret by a factor of $\sqrt{SA/C}$, in any communicating MDP with $S$ states, $A$ actions, and $C$ classes, which corresponds to a massive improvement when $C \ll SA$. To the best of our knowledge, this is the first work providing regret bounds for RL when an equivalence structure in the MDP is efficiently exploited. In the case of an unknown equivalence structure, we show through numerical experiments that C-UCRL combined with ApproxEquivalence outperforms UCRL2 in ergodic MDPs.