Learning The Minimum Action Distance

This paper presents a state representation framework for Markov decision processes (MDPs) that can be learned solely from state trajectories, requiring neither reward signals nor the actions executed by the agent. We propose learning the minimum action distance (MAD), defined as the minimum number of actions required to transition between states, as a fundamental metric that captures the underlying structure of an environment. MAD naturally enables critical downstream tasks such as goal-conditioned reinforcement learning and reward shaping by providing a dense, geometrically meaningful measure of progress. Our self-supervised learning approach constructs an embedding space where the distances between embedded state pairs correspond to their MAD, accommodating both symmetric and asymmetric approximations. We evaluate the framework on a comprehensive suite of environments with known MAD values, encompassing both deterministic and stochastic dynamics, as well as discrete and continuous state spaces, and environments with noisy observations. Empirical results demonstrate that the proposed approach not only efficiently learns accurate MAD representations across these diverse settings but also significantly outperforms existing state representation methods in terms of representation quality.

Asymmetric Norms to Approximate the Minimum Action Distance

This paper presents a state representation for reward-free Markov decision processes. The idea is to learn, in a self-supervised manner, an embedding space where distances between pairs of embedded states correspond to the minimum number of actions needed to transition between them. Unlike previous methods, our approach incorporates an asymmetric norm parametrization, enabling accurate approximations of minimum action distances in environments with inherent asymmetry. We show how this representation can be leveraged to learn goal-conditioned policies, providing a notion of similarity between states and goals and a useful heuristic distance to guide planning. To validate our approach, we conduct empirical experiments on both symmetric and asymmetric environments. Our results show that our asymmetric norm parametrization performs comparably to symmetric norms in symmetric environments and surpasses symmetric norms in asymmetric environments.

State Representation Learning for Goal-Conditioned Reinforcement Learning

This paper presents a novel state representation for reward-free Markov decision processes. The idea is to learn, in a self-supervised manner, an embedding space where distances between pairs of embedded states correspond to the minimum number of actions needed to transition between them. Compared to previous methods, our approach does not require any domain knowledge, learning from offline and unlabeled data. We show how this representation can be leveraged to learn goal-conditioned policies, providing a notion of similarity between states and goals and a useful heuristic distance to guide planning and reinforcement learning algorithms. Finally, we empirically validate our method in classic control domains and multi-goal environments, demonstrating that our method can successfully learn representations in large and/or continuous domains.

Hierarchical Representation Learning for Markov Decision Processes

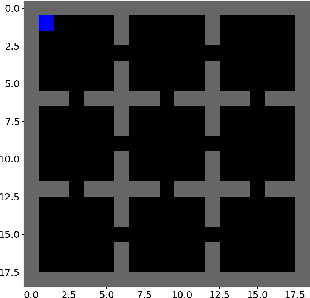
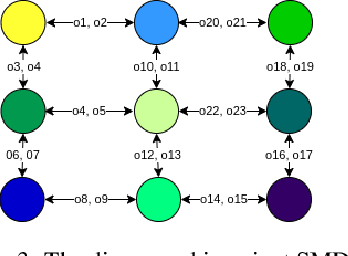
In this paper we present a novel method for learning hierarchical representations of Markov decision processes. Our method works by partitioning the state space into subsets, and defines subtasks for performing transitions between the partitions. We formulate the problem of partitioning the state space as an optimization problem that can be solved using gradient descent given a set of sampled trajectories, making our method suitable for high-dimensional problems with large state spaces. We empirically validate the method, by showing that it can successfully learn a useful hierarchical representation in a navigation domain. Once learned, the hierarchical representation can be used to solve different tasks in the given domain, thus generalizing knowledge across tasks.

Hierarchical reinforcement learning for efficient exploration and transfer

Sparse-reward domains are challenging for reinforcement learning algorithms since significant exploration is needed before encountering reward for the first time. Hierarchical reinforcement learning can facilitate exploration by reducing the number of decisions necessary before obtaining a reward. In this paper, we present a novel hierarchical reinforcement learning framework based on the compression of an invariant state space that is common to a range of tasks. The algorithm introduces subtasks which consist of moving between the state partitions induced by the compression. Results indicate that the algorithm can successfully solve complex sparse-reward domains, and transfer knowledge to solve new, previously unseen tasks more quickly.