A functional mirror ascent view of policy gradient methods with function approximation

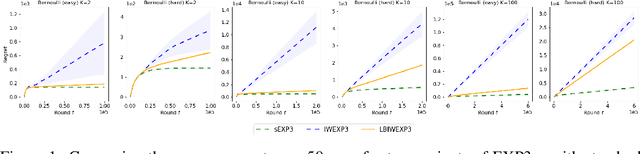
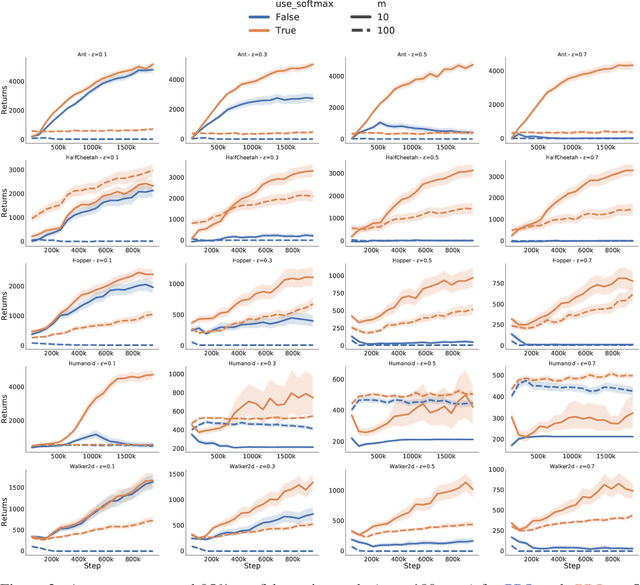
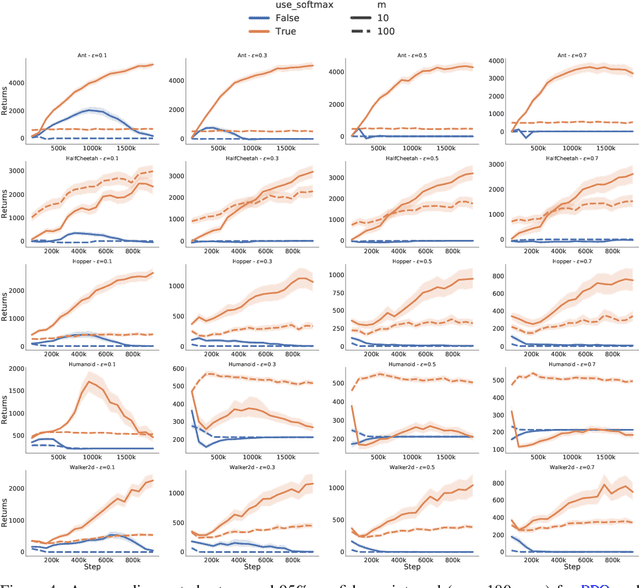
We use functional mirror ascent to propose a general framework (referred to as FMA-PG) for designing policy gradient methods. The functional perspective distinguishes between a policy's functional representation (what are its sufficient statistics) and its parameterization (how are these statistics represented) and naturally results in computationally efficient off-policy updates. For simple policy parameterizations, the FMA-PG framework ensures that the optimal policy is a fixed point of the updates. It also allows us to handle complex policy parameterizations (e.g., neural networks) while guaranteeing policy improvement. Our framework unifies several PG methods and opens the way for designing sample-efficient variants of existing methods. Moreover, it recovers important implementation heuristics (e.g., using forward vs reverse KL divergence) in a principled way. With a softmax functional representation, FMA-PG results in a variant of TRPO with additional desirable properties. It also suggests an improved variant of PPO, whose robustness and efficiency we empirically demonstrate on MuJoCo. Via experiments on simple reinforcement learning problems, we evaluate algorithms instantiated by FMA-PG.

Hierarchical Representation Learning for Markov Decision Processes

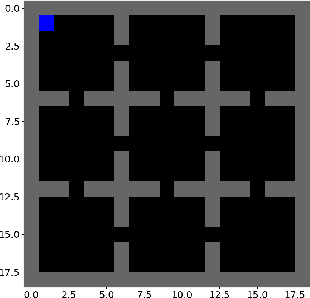
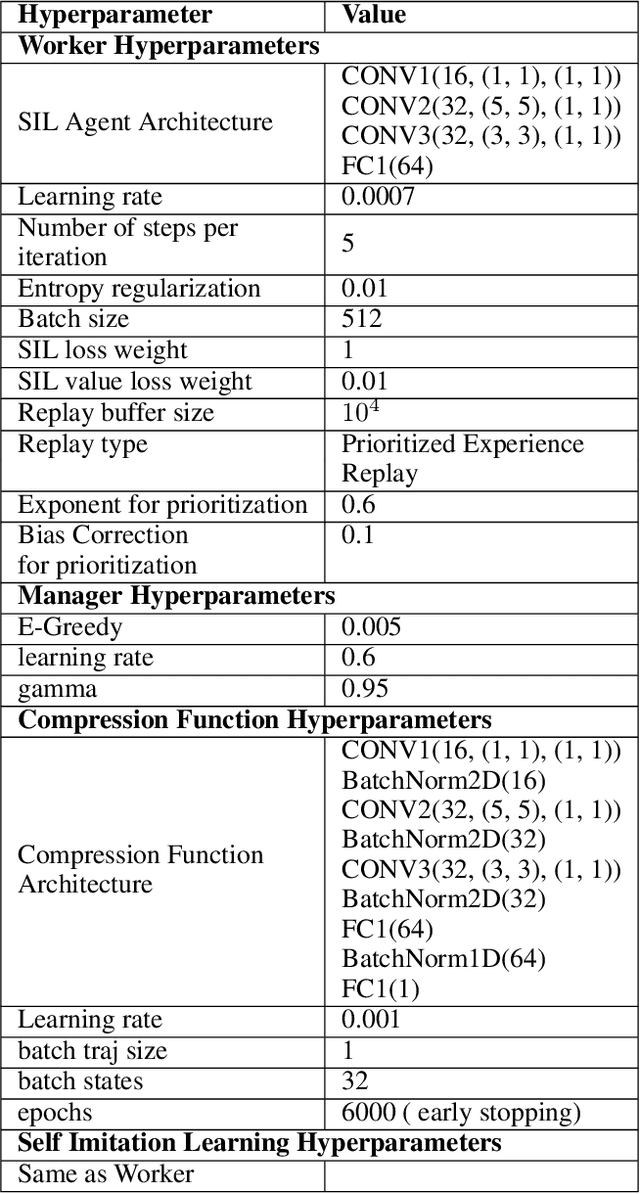
In this paper we present a novel method for learning hierarchical representations of Markov decision processes. Our method works by partitioning the state space into subsets, and defines subtasks for performing transitions between the partitions. We formulate the problem of partitioning the state space as an optimization problem that can be solved using gradient descent given a set of sampled trajectories, making our method suitable for high-dimensional problems with large state spaces. We empirically validate the method, by showing that it can successfully learn a useful hierarchical representation in a navigation domain. Once learned, the hierarchical representation can be used to solve different tasks in the given domain, thus generalizing knowledge across tasks.

Hierarchical reinforcement learning for efficient exploration and transfer

Sparse-reward domains are challenging for reinforcement learning algorithms since significant exploration is needed before encountering reward for the first time. Hierarchical reinforcement learning can facilitate exploration by reducing the number of decisions necessary before obtaining a reward. In this paper, we present a novel hierarchical reinforcement learning framework based on the compression of an invariant state space that is common to a range of tasks. The algorithm introduces subtasks which consist of moving between the state partitions induced by the compression. Results indicate that the algorithm can successfully solve complex sparse-reward domains, and transfer knowledge to solve new, previously unseen tasks more quickly.

Lifelong Control of Off-grid Microgrid with Model Based Reinforcement Learning

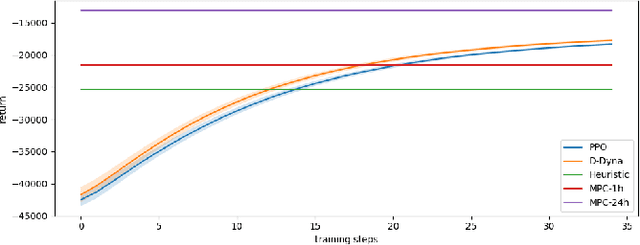
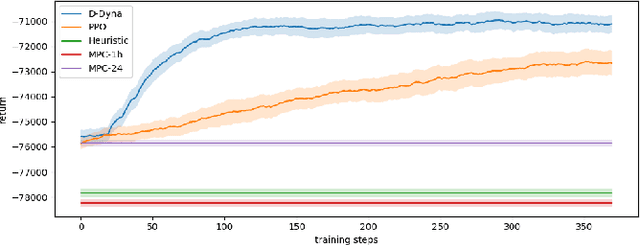
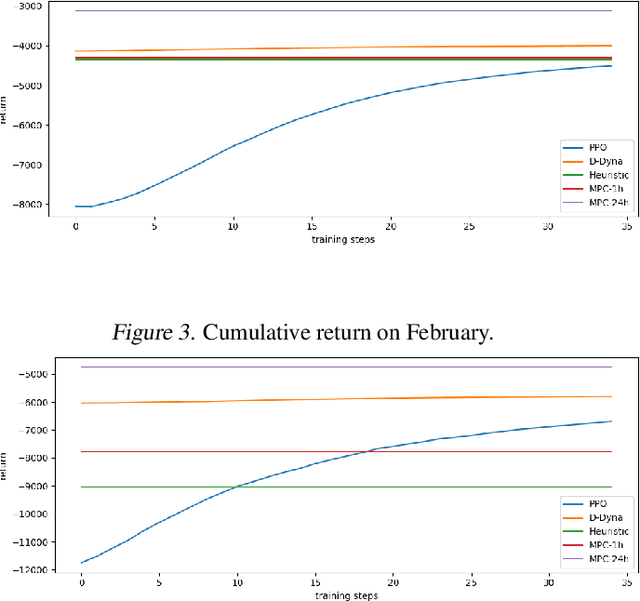
The lifelong control problem of an off-grid microgrid is composed of two tasks, namely estimation of the condition of the microgrid devices and operational planning accounting for the uncertainties by forecasting the future consumption and the renewable production. The main challenge for the effective control arises from the various changes that take place over time. In this paper, we present an open-source reinforcement framework for the modeling of an off-grid microgrid for rural electrification. The lifelong control problem of an isolated microgrid is formulated as a Markov Decision Process (MDP). We categorize the set of changes that can occur in progressive and abrupt changes. We propose a novel model based reinforcement learning algorithm that is able to address both types of changes. In particular the proposed algorithm demonstrates generalisation properties, transfer capabilities and better robustness in case of fast-changing system dynamics. The proposed algorithm is compared against a rule-based policy and a model predictive controller with look-ahead. The results show that the trained agent is able to outperform both benchmarks in the lifelong setting where the system dynamics are changing over time.

Adaptive Smoothing Path Integral Control

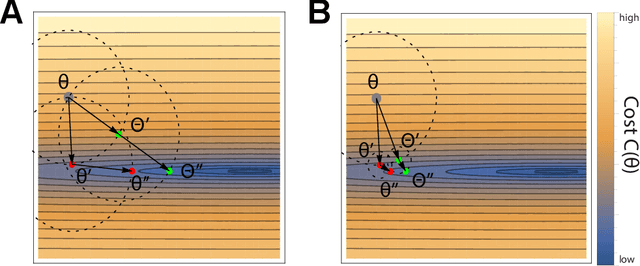
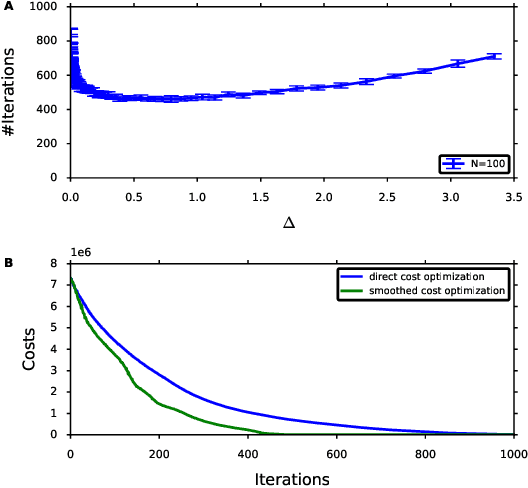
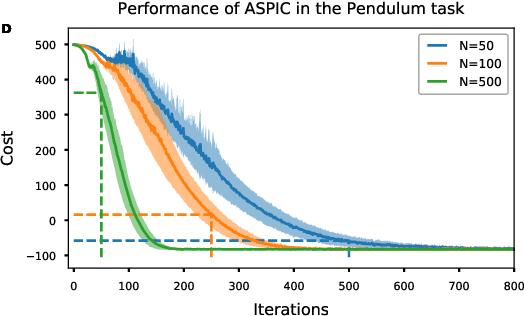
In Path Integral control problems a representation of an optimally controlled dynamical system can be formally computed and serve as a guidepost to learn a parametrized policy. The Path Integral Cross-Entropy (PICE) method tries to exploit this, but is hampered by poor sample efficiency. We propose a model-free algorithm called ASPIC (Adaptive Smoothing of Path Integral Control) that applies an inf-convolution to the cost function to speedup convergence of policy optimization. We identify PICE as the infinite smoothing limit of such technique and show that the sample efficiency problems that PICE suffers disappear for finite levels of smoothing. For zero smoothing this method becomes a greedy optimization of the cost, which is the standard approach in current reinforcement learning. We show analytically and empirically that intermediate levels of smoothing are optimal, which renders the new method superior to both PICE and direct cost-optimization.

Recurrent Neural Networks with Flexible Gates using Kernel Activation Functions

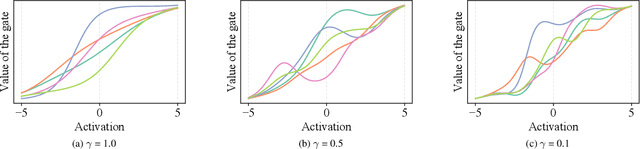
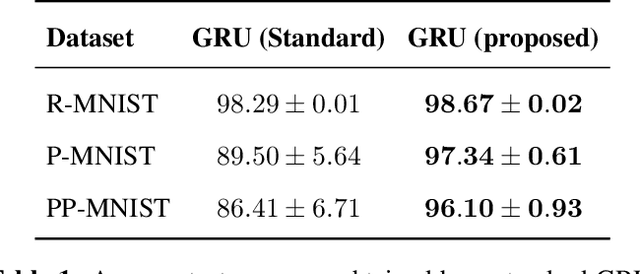
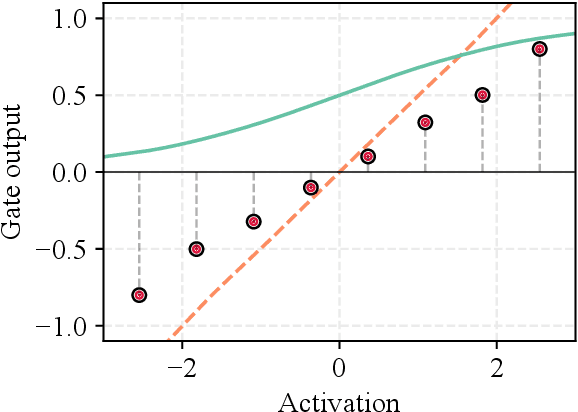
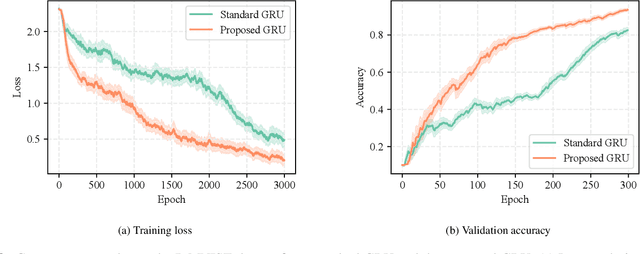
Gated recurrent neural networks have achieved remarkable results in the analysis of sequential data. Inside these networks, gates are used to control the flow of information, allowing to model even very long-term dependencies in the data. In this paper, we investigate whether the original gate equation (a linear projection followed by an element-wise sigmoid) can be improved. In particular, we design a more flexible architecture, with a small number of adaptable parameters, which is able to model a wider range of gating functions than the classical one. To this end, we replace the sigmoid function in the standard gate with a non-parametric formulation extending the recently proposed kernel activation function (KAF), with the addition of a residual skip-connection. A set of experiments on sequential variants of the MNIST dataset shows that the adoption of this novel gate allows to improve accuracy with a negligible cost in terms of computational power and with a large speed-up in the number of training iterations.

Kafnets: kernel-based non-parametric activation functions for neural networks

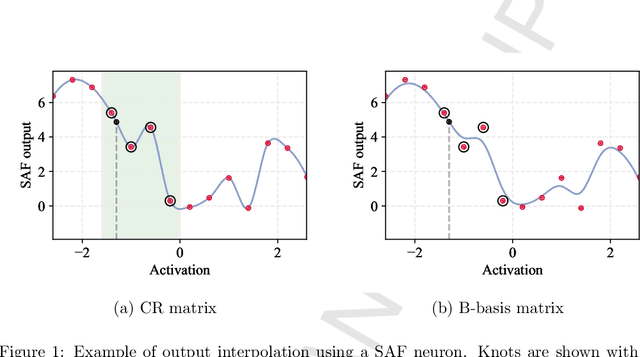
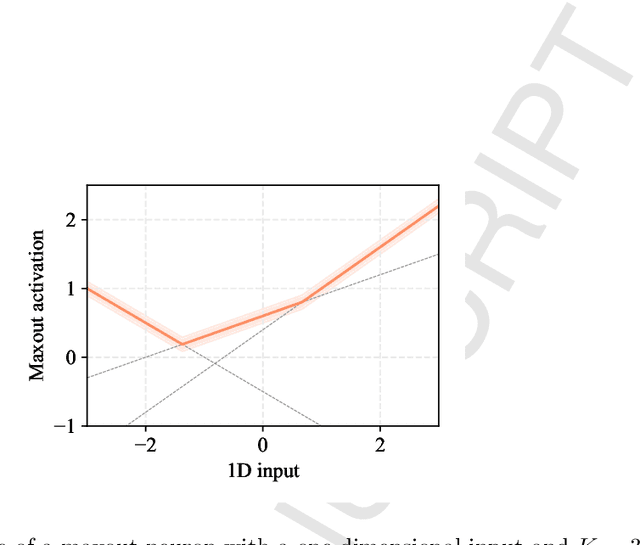
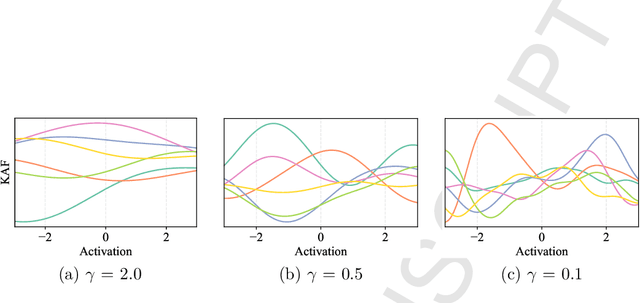
Neural networks are generally built by interleaving (adaptable) linear layers with (fixed) nonlinear activation functions. To increase their flexibility, several authors have proposed methods for adapting the activation functions themselves, endowing them with varying degrees of flexibility. None of these approaches, however, have gained wide acceptance in practice, and research in this topic remains open. In this paper, we introduce a novel family of flexible activation functions that are based on an inexpensive kernel expansion at every neuron. Leveraging over several properties of kernel-based models, we propose multiple variations for designing and initializing these kernel activation functions (KAFs), including a multidimensional scheme allowing to nonlinearly combine information from different paths in the network. The resulting KAFs can approximate any mapping defined over a subset of the real line, either convex or nonconvex. Furthermore, they are smooth over their entire domain, linear in their parameters, and they can be regularized using any known scheme, including the use of $\ell_1$ penalties to enforce sparseness. To the best of our knowledge, no other known model satisfies all these properties simultaneously. In addition, we provide a relatively complete overview on alternative techniques for adapting the activation functions, which is currently lacking in the literature. A large set of experiments validates our proposal.