Adaptive Smoothing Path Integral Control

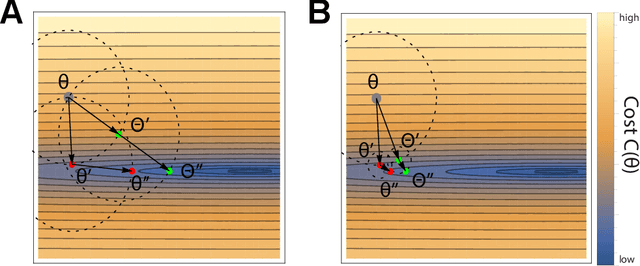
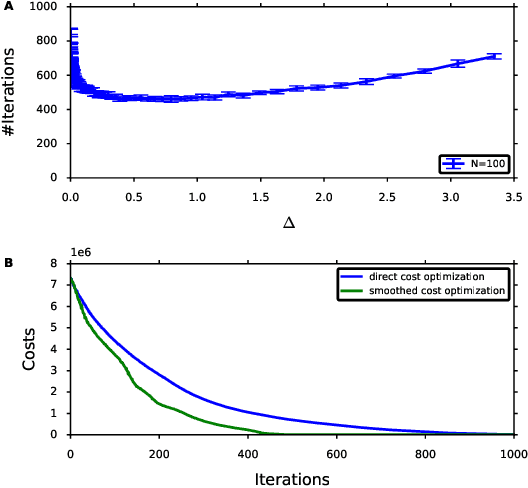
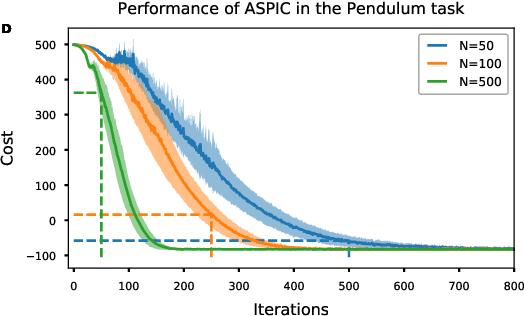
In Path Integral control problems a representation of an optimally controlled dynamical system can be formally computed and serve as a guidepost to learn a parametrized policy. The Path Integral Cross-Entropy (PICE) method tries to exploit this, but is hampered by poor sample efficiency. We propose a model-free algorithm called ASPIC (Adaptive Smoothing of Path Integral Control) that applies an inf-convolution to the cost function to speedup convergence of policy optimization. We identify PICE as the infinite smoothing limit of such technique and show that the sample efficiency problems that PICE suffers disappear for finite levels of smoothing. For zero smoothing this method becomes a greedy optimization of the cost, which is the standard approach in current reinforcement learning. We show analytically and empirically that intermediate levels of smoothing are optimal, which renders the new method superior to both PICE and direct cost-optimization.

On the role of synaptic stochasticity in training low-precision neural networks

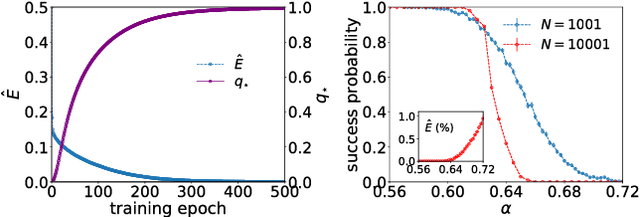
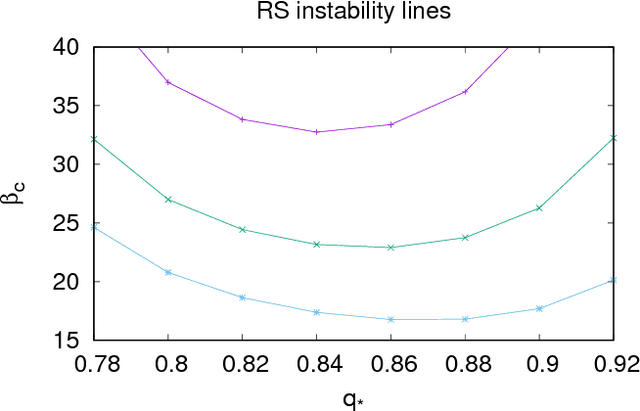
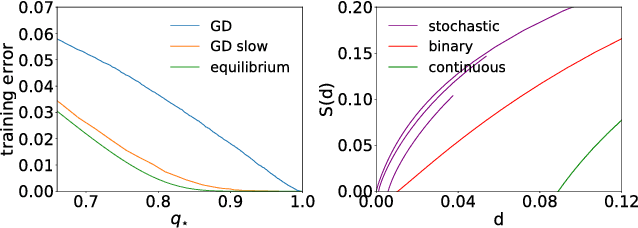
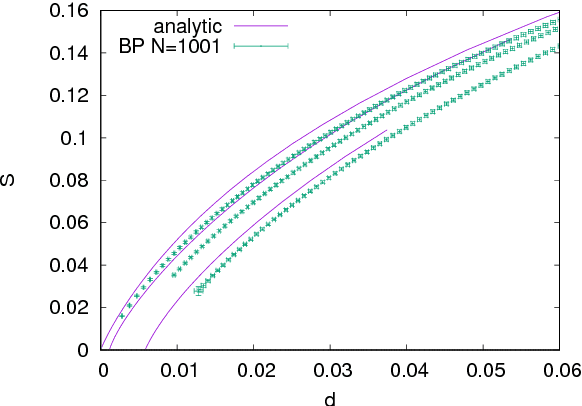
Stochasticity and limited precision of synaptic weights in neural network models are key aspects of both biological and hardware modeling of learning processes. Here we show that a neural network model with stochastic binary weights naturally gives prominence to exponentially rare dense regions of solutions with a number of desirable properties such as robustness and good generalization performance, while typical solutions are isolated and hard to find. Binary solutions of the standard perceptron problem are obtained from a simple gradient descent procedure on a set of real values parametrizing a probability distribution over the binary synapses. Both analytical and numerical results are presented. An algorithmic extension aimed at training discrete deep neural networks is also investigated.

Real-Time Stochastic Optimal Control for Multi-agent Quadrotor Systems

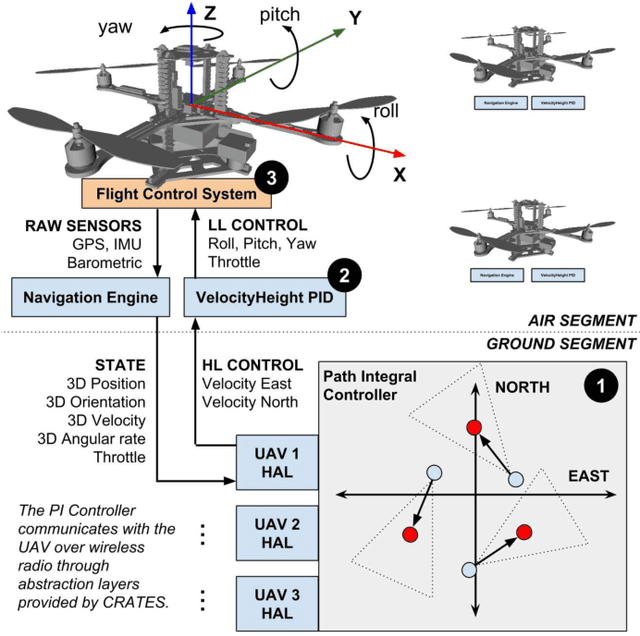
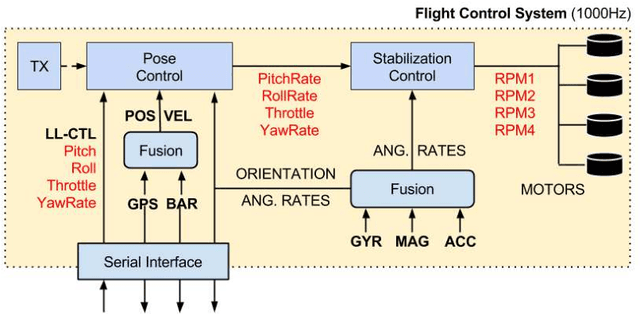
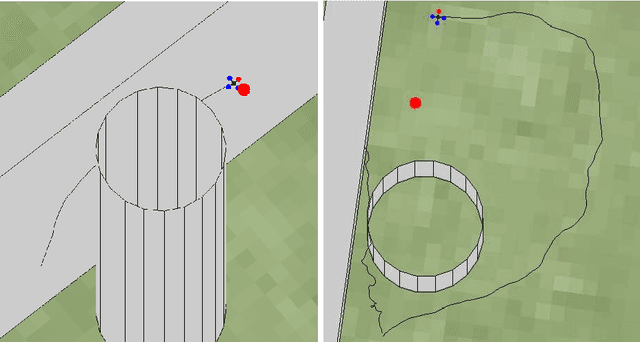
This paper presents a novel method for controlling teams of unmanned aerial vehicles using Stochastic Optimal Control (SOC) theory. The approach consists of a centralized high-level planner that computes optimal state trajectories as velocity sequences, and a platform-specific low-level controller which ensures that these velocity sequences are met. The planning task is expressed as a centralized path-integral control problem, for which optimal control computation corresponds to a probabilistic inference problem that can be solved by efficient sampling methods. Through simulation we show that our SOC approach (a) has significant benefits compared to deterministic control and other SOC methods in multimodal problems with noise-dependent optimal solutions, (b) is capable of controlling a large number of platforms in real-time, and (c) yields collective emergent behaviour in the form of flight formations. Finally, we show that our approach works for real platforms, by controlling a team of three quadrotors in outdoor conditions.

Latent Kullback Leibler Control for Continuous-State Systems using Probabilistic Graphical Models

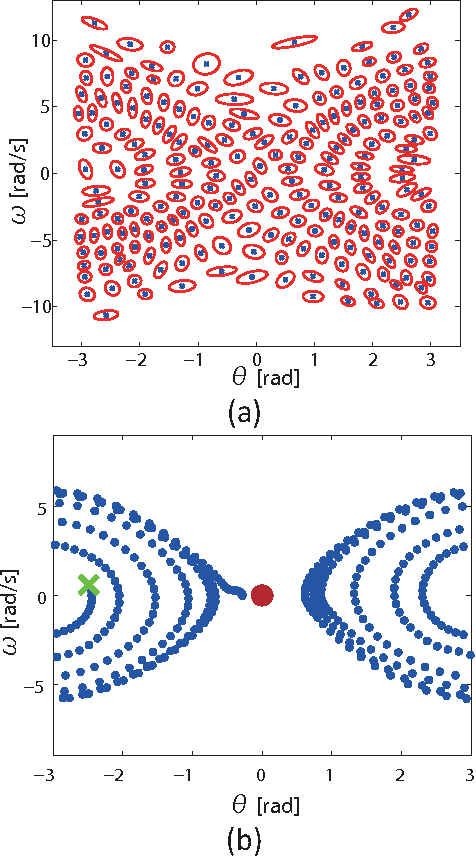
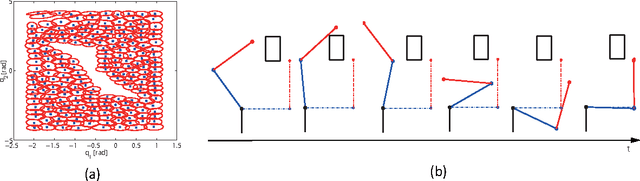
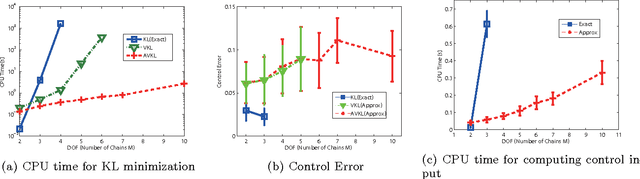
Kullback Leibler (KL) control problems allow for efficient computation of optimal control by solving a principal eigenvector problem. However, direct applicability of such framework to continuous state-action systems is limited. In this paper, we propose to embed a KL control problem in a probabilistic graphical model where observed variables correspond to the continuous (possibly high-dimensional) state of the system and latent variables correspond to a discrete (low-dimensional) representation of the state amenable for KL control computation. We present two examples of this approach. The first one uses standard hidden Markov models (HMMs) and computes exact optimal control, but is only applicable to low-dimensional systems. The second one uses factorial HMMs, it is scalable to higher dimensional problems, but control computation is approximate. We illustrate both examples in several robot motor control tasks.

The Variational Garrote

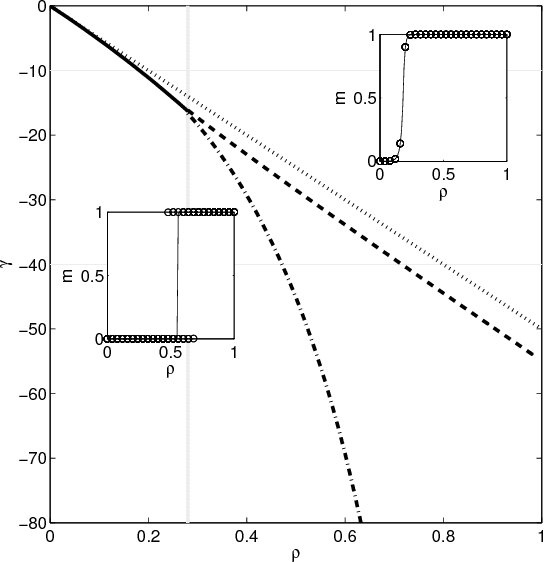
In this paper, we present a new variational method for sparse regression using $L_0$ regularization. The variational parameters appear in the approximate model in a way that is similar to Breiman's Garrote model. We refer to this method as the variational Garrote (VG). We show that the combination of the variational approximation and $L_0$ regularization has the effect of making the problem effectively of maximal rank even when the number of samples is small compared to the number of variables. The VG is compared numerically with the Lasso method, ridge regression and the recently introduced paired mean field method (PMF) (M. Titsias & M. L\'azaro-Gredilla., NIPS 2012). Numerical results show that the VG and PMF yield more accurate predictions and more accurately reconstruct the true model than the other methods. It is shown that the VG finds correct solutions when the Lasso solution is inconsistent due to large input correlations. Globally, VG is significantly faster than PMF and tends to perform better as the problems become denser and in problems with strongly correlated inputs. The naive implementation of the VG scales cubic with the number of features. By introducing Lagrange multipliers we obtain a dual formulation of the problem that scales cubic in the number of samples, but close to linear in the number of features.

Dynamic Policy Programming

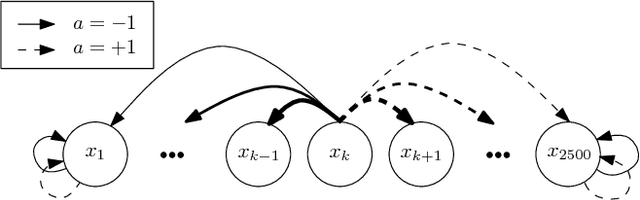
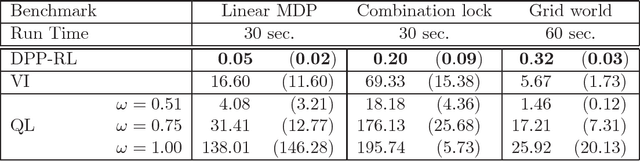
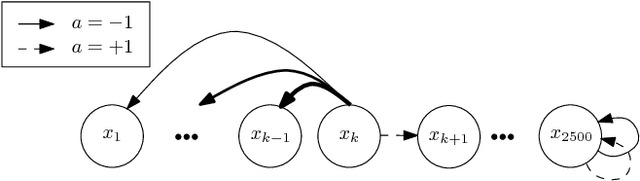
In this paper, we propose a novel policy iteration method, called dynamic policy programming (DPP), to estimate the optimal policy in the infinite-horizon Markov decision processes. We prove the finite-iteration and asymptotic l\infty-norm performance-loss bounds for DPP in the presence of approximation/estimation error. The bounds are expressed in terms of the l\infty-norm of the average accumulated error as opposed to the l\infty-norm of the error in the case of the standard approximate value iteration (AVI) and the approximate policy iteration (API). This suggests that DPP can achieve a better performance than AVI and API since it averages out the simulation noise caused by Monte-Carlo sampling throughout the learning process. We examine this theoretical results numerically by com- paring the performance of the approximate variants of DPP with existing reinforcement learning (RL) methods on different problem domains. Our results show that, in all cases, DPP-based algorithms outperform other RL methods by a wide margin.

Sufficient conditions for convergence of the Sum-Product Algorithm

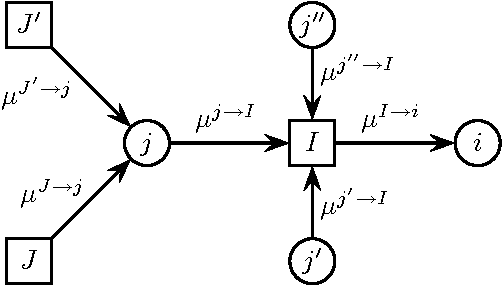
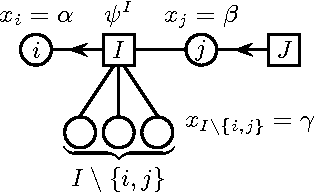
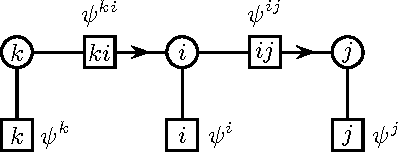
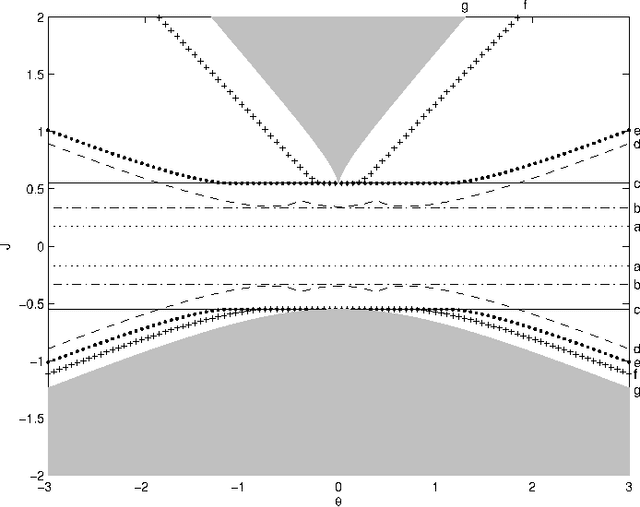
We derive novel conditions that guarantee convergence of the Sum-Product algorithm (also known as Loopy Belief Propagation or simply Belief Propagation) to a unique fixed point, irrespective of the initial messages. The computational complexity of the conditions is polynomial in the number of variables. In contrast with previously existing conditions, our results are directly applicable to arbitrary factor graphs (with discrete variables) and are shown to be valid also in the case of factors containing zeros, under some additional conditions. We compare our bounds with existing ones, numerically and, if possible, analytically. For binary variables with pairwise interactions, we derive sufficient conditions that take into account local evidence (i.e., single variable factors) and the type of pair interactions (attractive or repulsive). It is shown empirically that this bound outperforms existing bounds.