Latent Kullback Leibler Control for Continuous-State Systems using Probabilistic Graphical Models
Paper and Code
Aug 27, 2014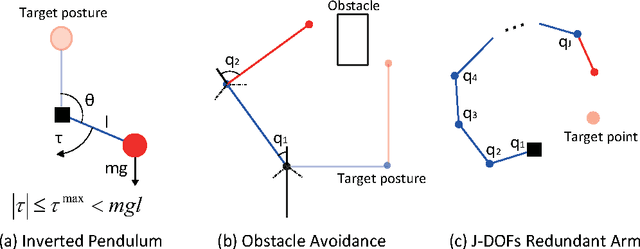
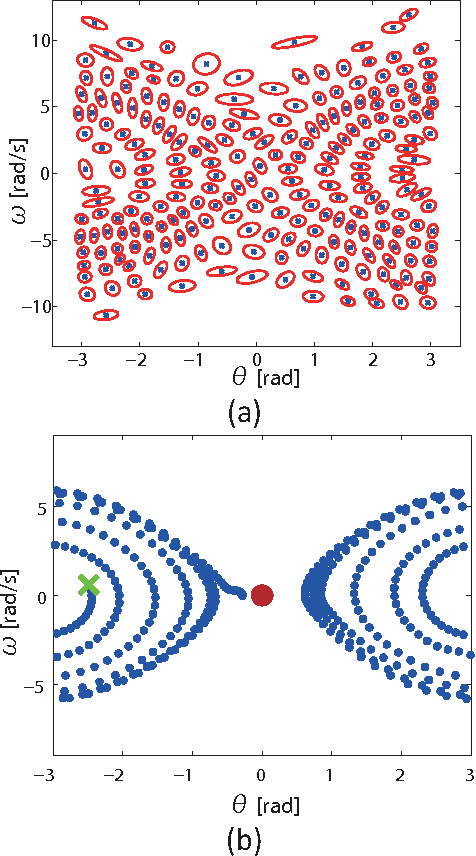
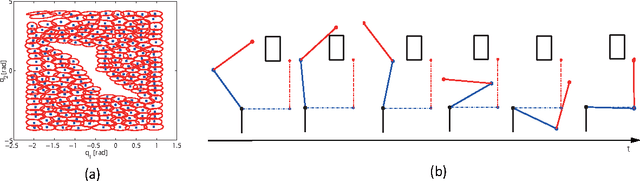
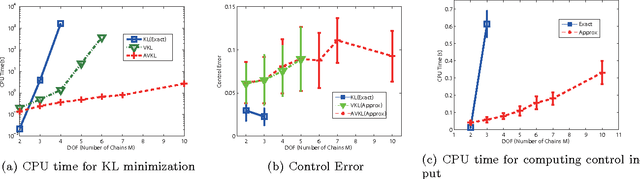
Kullback Leibler (KL) control problems allow for efficient computation of optimal control by solving a principal eigenvector problem. However, direct applicability of such framework to continuous state-action systems is limited. In this paper, we propose to embed a KL control problem in a probabilistic graphical model where observed variables correspond to the continuous (possibly high-dimensional) state of the system and latent variables correspond to a discrete (low-dimensional) representation of the state amenable for KL control computation. We present two examples of this approach. The first one uses standard hidden Markov models (HMMs) and computes exact optimal control, but is only applicable to low-dimensional systems. The second one uses factorial HMMs, it is scalable to higher dimensional problems, but control computation is approximate. We illustrate both examples in several robot motor control tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge