A distributional simplicity bias in the learning dynamics of transformers

The remarkable capability of over-parameterised neural networks to generalise effectively has been explained by invoking a ``simplicity bias'': neural networks prevent overfitting by initially learning simple classifiers before progressing to more complex, non-linear functions. While simplicity biases have been described theoretically and experimentally in feed-forward networks for supervised learning, the extent to which they also explain the remarkable success of transformers trained with self-supervised techniques remains unclear. In our study, we demonstrate that transformers, trained on natural language data, also display a simplicity bias. Specifically, they sequentially learn many-body interactions among input tokens, reaching a saturation point in the prediction error for low-degree interactions while continuing to learn high-degree interactions. To conduct this analysis, we develop a procedure to generate \textit{clones} of a given natural language data set, which rigorously capture the interactions between tokens up to a specified order. This approach opens up the possibilities of studying how interactions of different orders in the data affect learning, in natural language processing and beyond.

Learning from higher-order statistics, efficiently: hypothesis tests, random features, and neural networks

Neural networks excel at discovering statistical patterns in high-dimensional data sets. In practice, higher-order cumulants, which quantify the non-Gaussian correlations between three or more variables, are particularly important for the performance of neural networks. But how efficient are neural networks at extracting features from higher-order cumulants? We study this question in the spiked cumulant model, where the statistician needs to recover a privileged direction or "spike" from the order-$p\ge 4$ cumulants of~$d$-dimensional inputs. We first characterise the fundamental statistical and computational limits of recovering the spike by analysing the number of samples~$n$ required to strongly distinguish between inputs from the spiked cumulant model and isotropic Gaussian inputs. We find that statistical distinguishability requires $n\gtrsim d$ samples, while distinguishing the two distributions in polynomial time requires $n \gtrsim d^2$ samples for a wide class of algorithms, i.e. those covered by the low-degree conjecture. These results suggest the existence of a wide statistical-to-computational gap in this problem. Numerical experiments show that neural networks learn to distinguish the two distributions with quadratic sample complexity, while "lazy" methods like random features are not better than random guessing in this regime. Our results show that neural networks extract information from higher-order correlations in the spiked cumulant model efficiently, and reveal a large gap in the amount of data required by neural networks and random features to learn from higher-order cumulants.

Optimal inference of a generalised Potts model by single-layer transformers with factored attention

Transformers are the type of neural networks that has revolutionised natural language processing and protein science. Their key building block is a mechanism called self-attention which is trained to predict missing words in sentences. Despite the practical success of transformers in applications it remains unclear what self-attention learns from data, and how. Here, we give a precise analytical and numerical characterisation of transformers trained on data drawn from a generalised Potts model with interactions between sites and Potts colours. While an off-the-shelf transformer requires several layers to learn this distribution, we show analytically that a single layer of self-attention with a small modification can learn the Potts model exactly in the limit of infinite sampling. We show that this modified self-attention, that we call ``factored'', has the same functional form as the conditional probability of a Potts spin given the other spins, compute its generalisation error using the replica method from statistical physics, and derive an exact mapping to pseudo-likelihood methods for solving the inverse Ising and Potts problem.

Optimal transfer protocol by incremental layer defrosting

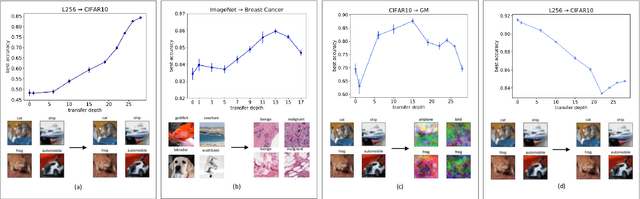
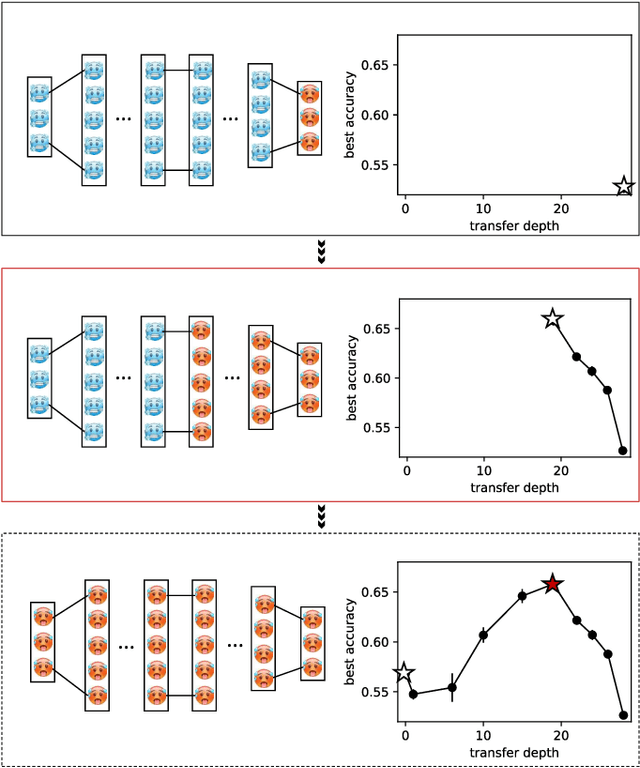
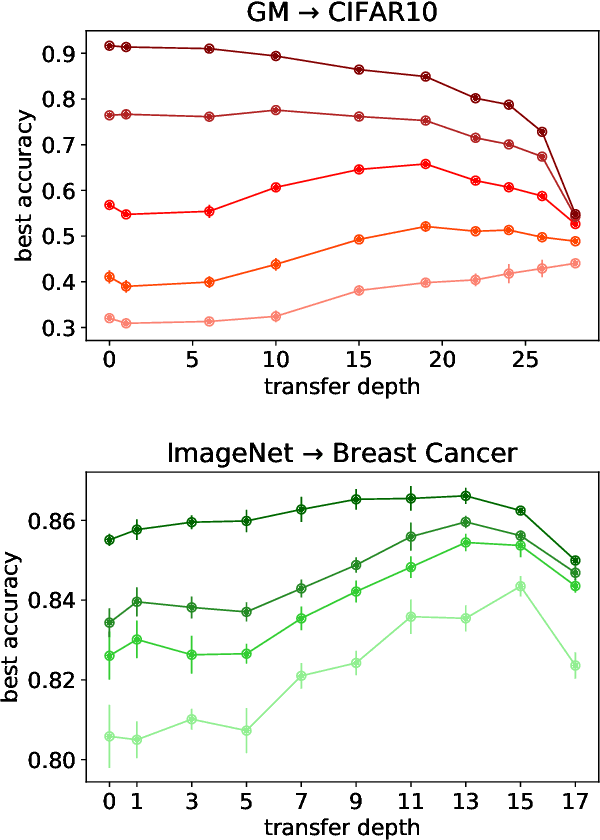
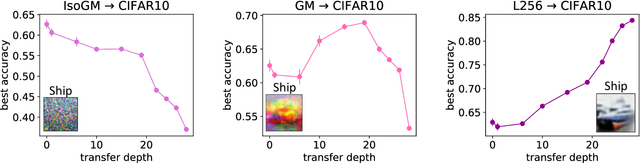
Transfer learning is a powerful tool enabling model training with limited amounts of data. This technique is particularly useful in real-world problems where data availability is often a serious limitation. The simplest transfer learning protocol is based on ``freezing" the feature-extractor layers of a network pre-trained on a data-rich source task, and then adapting only the last layers to a data-poor target task. This workflow is based on the assumption that the feature maps of the pre-trained model are qualitatively similar to the ones that would have been learned with enough data on the target task. In this work, we show that this protocol is often sub-optimal, and the largest performance gain may be achieved when smaller portions of the pre-trained network are kept frozen. In particular, we make use of a controlled framework to identify the optimal transfer depth, which turns out to depend non-trivially on the amount of available training data and on the degree of source-target task correlation. We then characterize transfer optimality by analyzing the internal representations of two networks trained from scratch on the source and the target task through multiple established similarity measures.

Inducing bias is simpler than you think

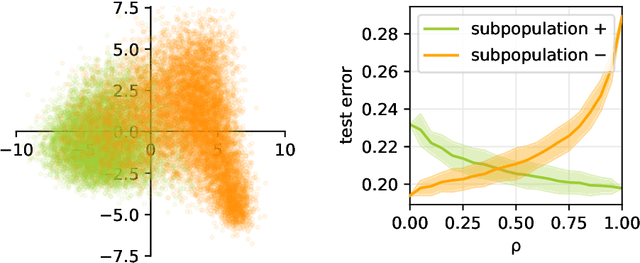
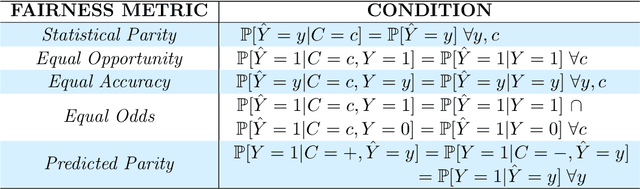
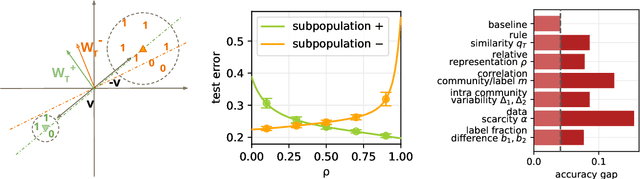
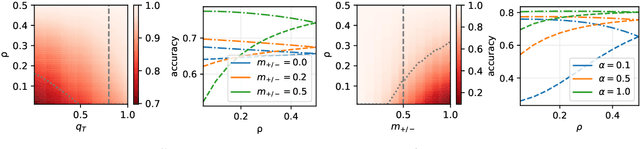
Machine learning may be oblivious to human bias but it is not immune to its perpetuation. Marginalisation and iniquitous group representation are often traceable in the very data used for training, and may be reflected or even enhanced by the learning models. To counter this, some of the model accuracy can be traded off for a secondary objective that helps prevent a specific type of bias. Multiple notions of fairness have been proposed to this end but recent studies show that some fairness criteria often stand in mutual competition. In the present work, we introduce a solvable high-dimensional model of data imbalance, where parametric control over the many bias-inducing factors allows for an extensive exploration of the bias inheritance mechanism. Through the tools of statistical physics, we analytically characterise the typical behaviour of learning models trained in our synthetic framework and find similar unfairness behaviours as those observed on more realistic data. However, we also identify a positive transfer effect between the different subpopulations within the data. This suggests that mixing data with different statistical properties could be helpful, provided the learning model is made aware of this structure. Finally, we analyse the issue of bias mitigation: by reweighing the various terms in the training loss, we indirectly minimise standard unfairness metrics and highlight their incompatibilities. Leveraging the insights on positive transfer, we also propose a theory-informed mitigation strategy, based on the introduction of coupled learning models. By allowing each model to specialise on a different community within the data, we find that multiple fairness criteria and high accuracy can be achieved simultaneously.

Gaussian Universality of Linear Classifiers with Random Labels in High-Dimension

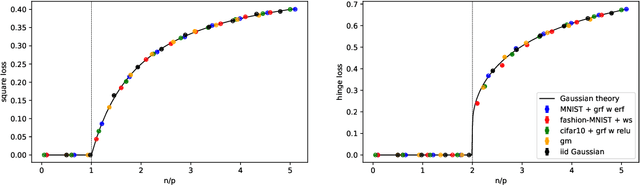
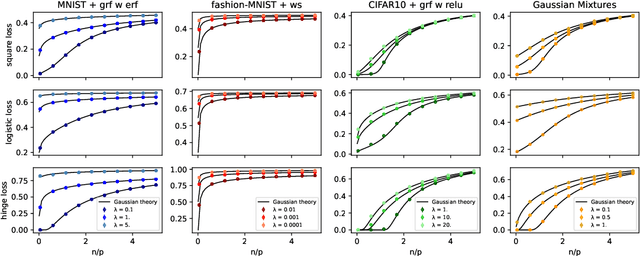
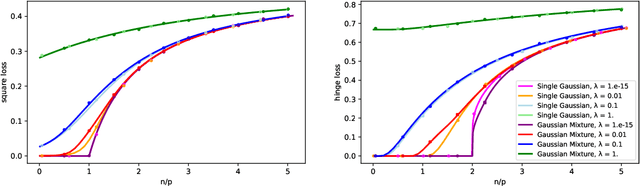
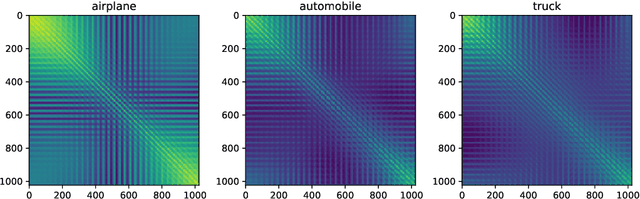
While classical in many theoretical settings, the assumption of Gaussian i.i.d. inputs is often perceived as a strong limitation in the analysis of high-dimensional learning. In this study, we redeem this line of work in the case of generalized linear classification with random labels. Our main contribution is a rigorous proof that data coming from a range of generative models in high-dimensions have the same minimum training loss as Gaussian data with corresponding data covariance. In particular, our theorem covers data created by an arbitrary mixture of homogeneous Gaussian clouds, as well as multi-modal generative neural networks. In the limit of vanishing regularization, we further demonstrate that the training loss is independent of the data covariance. Finally, we show that this universality property is observed in practice with real datasets and random labels.

Probing transfer learning with a model of synthetic correlated datasets

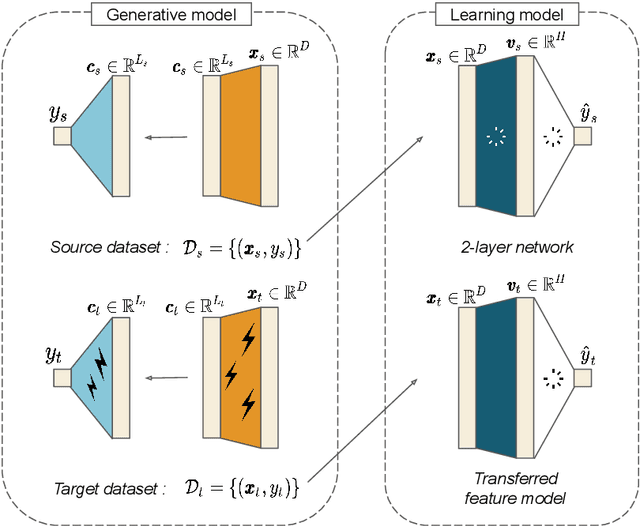
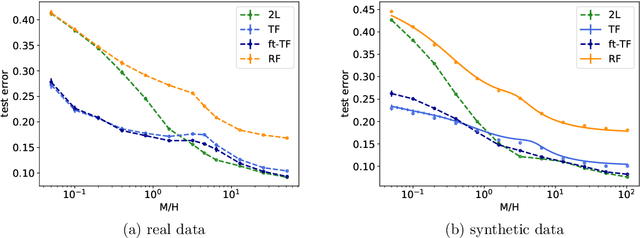
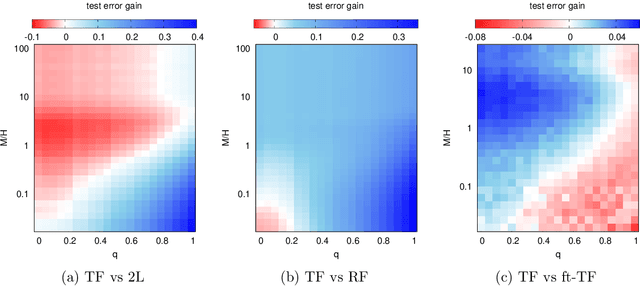
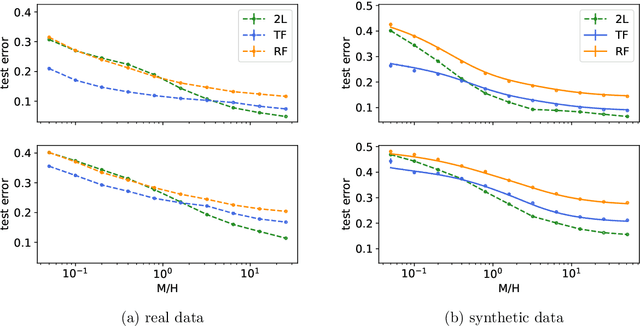
Transfer learning can significantly improve the sample efficiency of neural networks, by exploiting the relatedness between a data-scarce target task and a data-abundant source task. Despite years of successful applications, transfer learning practice often relies on ad-hoc solutions, while theoretical understanding of these procedures is still limited. In the present work, we re-think a solvable model of synthetic data as a framework for modeling correlation between data-sets. This setup allows for an analytic characterization of the generalization performance obtained when transferring the learned feature map from the source to the target task. Focusing on the problem of training two-layer networks in a binary classification setting, we show that our model can capture a range of salient features of transfer learning with real data. Moreover, by exploiting parametric control over the correlation between the two data-sets, we systematically investigate under which conditions the transfer of features is beneficial for generalization.

Generalisation error in learning with random features and the hidden manifold model

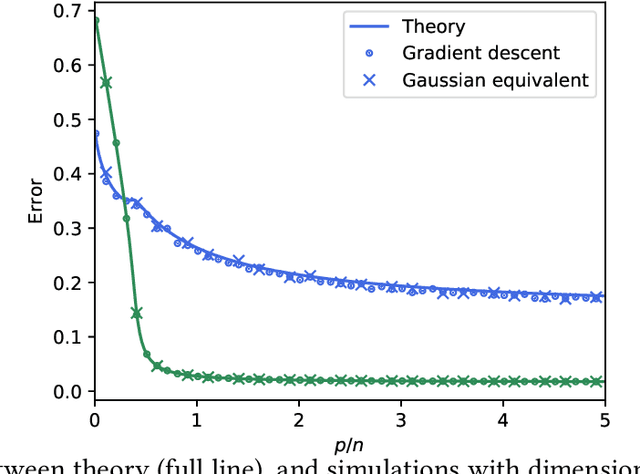
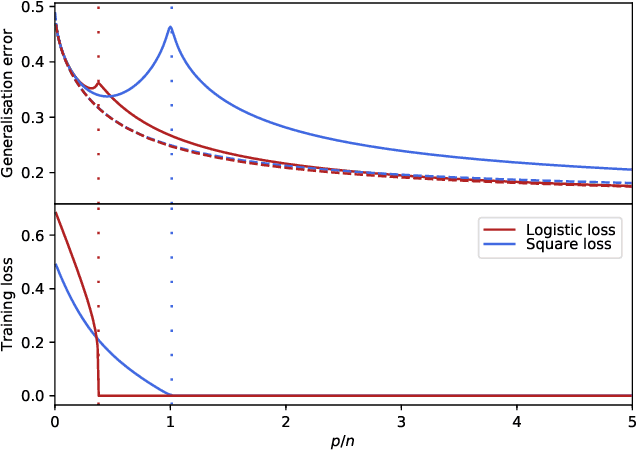
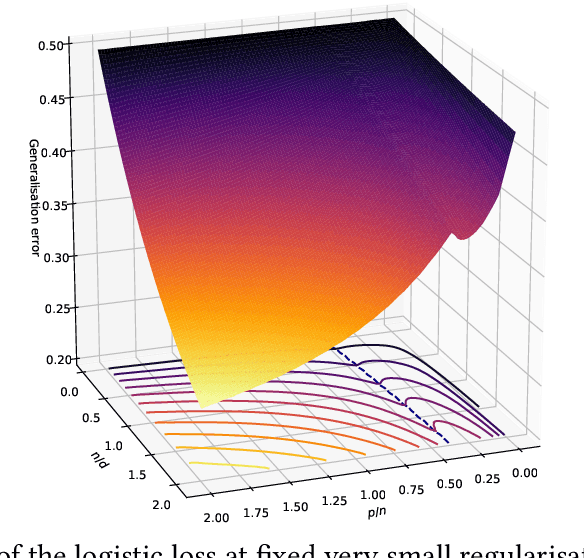
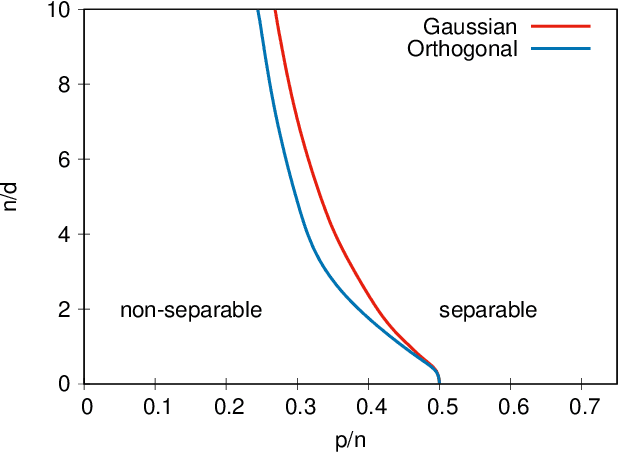
We study generalised linear regression and classification for a synthetically generated dataset encompassing different problems of interest, such as learning with random features, neural networks in the lazy training regime, and the hidden manifold model. We consider the high-dimensional regime and using the replica method from statistical physics, we provide a closed-form expression for the asymptotic generalisation performance in these problems, valid in both the under- and over-parametrised regimes and for a broad choice of generalised linear model loss functions. In particular, we show how to obtain analytically the so-called double descent behaviour for logistic regression with a peak at the interpolation threshold, we illustrate the superiority of orthogonal against random Gaussian projections in learning with random features, and discuss the role played by correlations in the data generated by the hidden manifold model. Beyond the interest in these particular problems, the theoretical formalism introduced in this manuscript provides a path to further extensions to more complex tasks.

Signal propagation in continuous approximations of binary neural networks

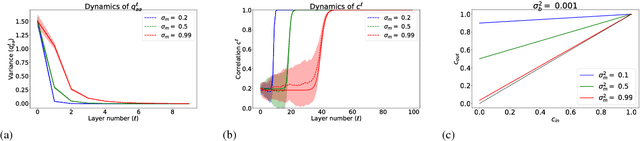
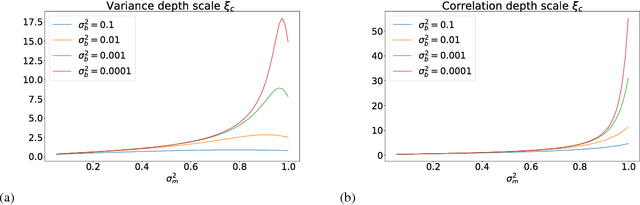
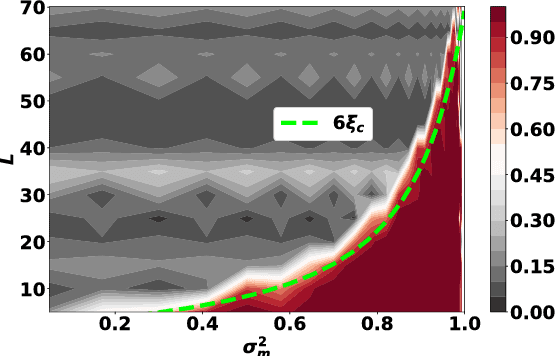
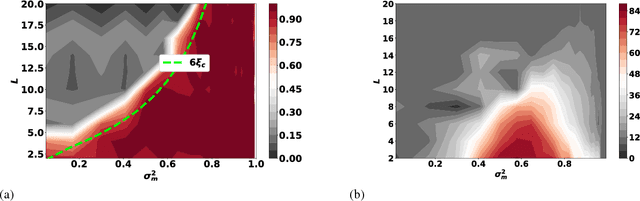
The training of stochastic neural network models with binary ($\pm1$) weights and activations via a deterministic and continuous surrogate network is investigated. We derive, using mean field theory, a set of scalar equations describing how input signals propagate through the surrogate network. The equations reveal that these continuous models exhibit an order to chaos transition, and the presence of depth scales that limit the maximum trainable depth. Moreover, we predict theoretically and confirm numerically, that common weight initialization schemes used in standard continuous networks, when applied to the mean values of the stochastic binary weights, yield poor training performance. This study shows that, contrary to common intuition, the means of the stochastic binary weights should be initialised close to $\pm 1$ for deeper networks to be trainable.

On the role of synaptic stochasticity in training low-precision neural networks

Stochasticity and limited precision of synaptic weights in neural network models are key aspects of both biological and hardware modeling of learning processes. Here we show that a neural network model with stochastic binary weights naturally gives prominence to exponentially rare dense regions of solutions with a number of desirable properties such as robustness and good generalization performance, while typical solutions are isolated and hard to find. Binary solutions of the standard perceptron problem are obtained from a simple gradient descent procedure on a set of real values parametrizing a probability distribution over the binary synapses. Both analytical and numerical results are presented. An algorithmic extension aimed at training discrete deep neural networks is also investigated.