Signal propagation in continuous approximations of binary neural networks
Paper and Code
Feb 01, 2019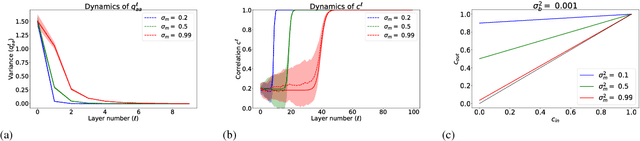
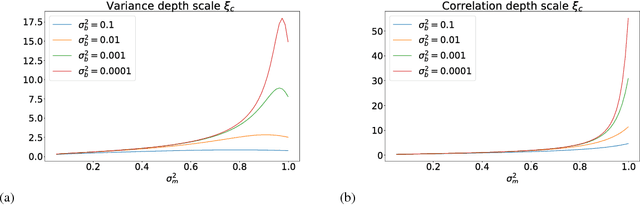
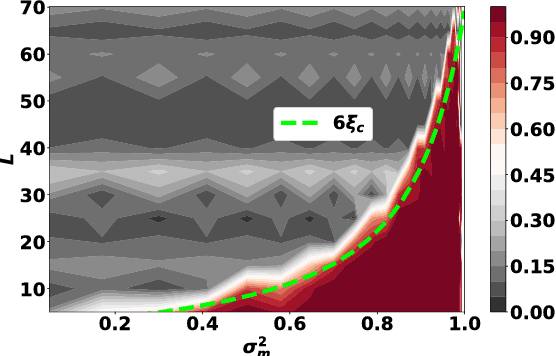
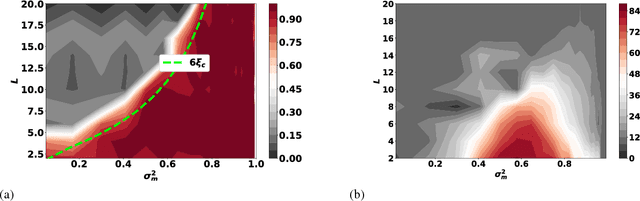
The training of stochastic neural network models with binary ($\pm1$) weights and activations via a deterministic and continuous surrogate network is investigated. We derive, using mean field theory, a set of scalar equations describing how input signals propagate through the surrogate network. The equations reveal that these continuous models exhibit an order to chaos transition, and the presence of depth scales that limit the maximum trainable depth. Moreover, we predict theoretically and confirm numerically, that common weight initialization schemes used in standard continuous networks, when applied to the mean values of the stochastic binary weights, yield poor training performance. This study shows that, contrary to common intuition, the means of the stochastic binary weights should be initialised close to $\pm 1$ for deeper networks to be trainable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge