Two failure modes of deep transformers and how to avoid them: a unified theory of signal propagation at initialisation

Finding the right initialisation for neural networks is crucial to ensure smooth training and good performance. In transformers, the wrong initialisation can lead to one of two failure modes of self-attention layers: rank collapse, where all tokens collapse into similar representations, and entropy collapse, where highly concentrated attention scores lead to training instability. While the right initialisation has been extensively studied in feed-forward networks, an exact description of signal propagation through a full transformer block has so far been lacking. Here, we provide an analytical theory of signal propagation through vanilla transformer blocks with self-attention layers, layer normalisation, skip connections and ReLU MLP. To treat the self-attention layer, we draw on a formal parallel with the Random Energy Model from statistical physics. We identify and characterise two regimes governed by the variance of the query and key initialisations: a low-variance regime, where we recover the known rank collapse behaviour; and a previously unexplored high-variance regime, where signal is preserved but \textit{entropy collapse} occurs. In the low-variance regime, we calculate the critical strength for the residual connection to ensure signal propagation. Our theory yields trainability diagrams that identify the correct choice of initialisation hyper-parameters for a given architecture. Experiments with BERT-style models trained on TinyStories validate our predictions. Our theoretical framework gives a unified perspective on the two failure modes of self-attention and gives quantitative predictions on the scale of both weights and residual connections that guarantees smooth training.

Generalization Dynamics of Linear Diffusion Models

Diffusion models trained on finite datasets with $N$ samples from a target distribution exhibit a transition from memorisation, where the model reproduces training examples, to generalisation, where it produces novel samples that reflect the underlying data distribution. Understanding this transition is key to characterising the sample efficiency and reliability of generative models, but our theoretical understanding of this transition is incomplete. Here, we analytically study the memorisation-to-generalisation transition in a simple model using linear denoisers, which allow explicit computation of test errors, sampling distributions, and Kullback-Leibler divergences between samples and target distribution. Using these measures, we predict that this transition occurs roughly when $N \asymp d$, the dimension of the inputs. When $N$ is smaller than the dimension of the inputs $d$, so that only a fraction of relevant directions of variation are present in the training data, we demonstrate how both regularization and early stopping help to prevent overfitting. For $N > d$, we find that the sampling distributions of linear diffusion models approach their optimum (measured by the Kullback-Leibler divergence) linearly with $d/N$, independent of the specifics of the data distribution. Our work clarifies how sample complexity governs generalisation in a simple model of diffusion-based generative models and provides insight into the training dynamics of linear denoisers.

Feature learning from non-Gaussian inputs: the case of Independent Component Analysis in high dimensions

Deep neural networks learn structured features from complex, non-Gaussian inputs, but the mechanisms behind this process remain poorly understood. Our work is motivated by the observation that the first-layer filters learnt by deep convolutional neural networks from natural images resemble those learnt by independent component analysis (ICA), a simple unsupervised method that seeks the most non-Gaussian projections of its inputs. This similarity suggests that ICA provides a simple, yet principled model for studying feature learning. Here, we leverage this connection to investigate the interplay between data structure and optimisation in feature learning for the most popular ICA algorithm, FastICA, and stochastic gradient descent (SGD), which is used to train deep networks. We rigorously establish that FastICA requires at least $n\gtrsim d^4$ samples to recover a single non-Gaussian direction from $d$-dimensional inputs on a simple synthetic data model. We show that vanilla online SGD outperforms FastICA, and prove that the optimal sample complexity $n \gtrsim d^2$ can be reached by smoothing the loss, albeit in a data-dependent way. We finally demonstrate the existence of a search phase for FastICA on ImageNet, and discuss how the strong non-Gaussianity of said images compensates for the poor sample complexity of FastICA.

On How Iterative Magnitude Pruning Discovers Local Receptive Fields in Fully Connected Neural Networks

Since its use in the Lottery Ticket Hypothesis, iterative magnitude pruning (IMP) has become a popular method for extracting sparse subnetworks that can be trained to high performance. Despite this, the underlying nature of IMP's general success remains unclear. One possibility is that IMP is especially capable of extracting and maintaining strong inductive biases. In support of this, recent work has shown that applying IMP to fully connected neural networks (FCNs) leads to the emergence of local receptive fields (RFs), an architectural feature present in mammalian visual cortex and convolutional neural networks. The question of how IMP is able to do this remains unanswered. Inspired by results showing that training FCNs on synthetic images with highly non-Gaussian statistics (e.g., sharp edges) is sufficient to drive the formation of local RFs, we hypothesize that IMP iteratively maximizes the non-Gaussian statistics present in the representations of FCNs, creating a feedback loop that enhances localization. We develop a new method for measuring the effect of individual weights on the statistics of the FCN representations ("cavity method"), which allows us to find evidence in support of this hypothesis. Our work, which is the first to study the effect IMP has on the representations of neural networks, sheds parsimonious light one way in which IMP can drive the formation of strong inductive biases.

A distributional simplicity bias in the learning dynamics of transformers

The remarkable capability of over-parameterised neural networks to generalise effectively has been explained by invoking a ``simplicity bias'': neural networks prevent overfitting by initially learning simple classifiers before progressing to more complex, non-linear functions. While simplicity biases have been described theoretically and experimentally in feed-forward networks for supervised learning, the extent to which they also explain the remarkable success of transformers trained with self-supervised techniques remains unclear. In our study, we demonstrate that transformers, trained on natural language data, also display a simplicity bias. Specifically, they sequentially learn many-body interactions among input tokens, reaching a saturation point in the prediction error for low-degree interactions while continuing to learn high-degree interactions. To conduct this analysis, we develop a procedure to generate \textit{clones} of a given natural language data set, which rigorously capture the interactions between tokens up to a specified order. This approach opens up the possibilities of studying how interactions of different orders in the data affect learning, in natural language processing and beyond.

Sliding down the stairs: how correlated latent variables accelerate learning with neural networks

Neural networks extract features from data using stochastic gradient descent (SGD). In particular, higher-order input cumulants (HOCs) are crucial for their performance. However, extracting information from the $p$th cumulant of $d$-dimensional inputs is computationally hard: the number of samples required to recover a single direction from an order-$p$ tensor (tensor PCA) using online SGD grows as $d^{p-1}$, which is prohibitive for high-dimensional inputs. This result raises the question of how neural networks extract relevant directions from the HOCs of their inputs efficiently. Here, we show that correlations between latent variables along the directions encoded in different input cumulants speed up learning from higher-order correlations. We show this effect analytically by deriving nearly sharp thresholds for the number of samples required by a single neuron to weakly-recover these directions using online SGD from a random start in high dimensions. Our analytical results are confirmed in simulations of two-layer neural networks and unveil a new mechanism for hierarchical learning in neural networks.

Learning from higher-order statistics, efficiently: hypothesis tests, random features, and neural networks

Neural networks excel at discovering statistical patterns in high-dimensional data sets. In practice, higher-order cumulants, which quantify the non-Gaussian correlations between three or more variables, are particularly important for the performance of neural networks. But how efficient are neural networks at extracting features from higher-order cumulants? We study this question in the spiked cumulant model, where the statistician needs to recover a privileged direction or "spike" from the order-$p\ge 4$ cumulants of~$d$-dimensional inputs. We first characterise the fundamental statistical and computational limits of recovering the spike by analysing the number of samples~$n$ required to strongly distinguish between inputs from the spiked cumulant model and isotropic Gaussian inputs. We find that statistical distinguishability requires $n\gtrsim d$ samples, while distinguishing the two distributions in polynomial time requires $n \gtrsim d^2$ samples for a wide class of algorithms, i.e. those covered by the low-degree conjecture. These results suggest the existence of a wide statistical-to-computational gap in this problem. Numerical experiments show that neural networks learn to distinguish the two distributions with quadratic sample complexity, while "lazy" methods like random features are not better than random guessing in this regime. Our results show that neural networks extract information from higher-order correlations in the spiked cumulant model efficiently, and reveal a large gap in the amount of data required by neural networks and random features to learn from higher-order cumulants.

The RL Perceptron: Generalisation Dynamics of Policy Learning in High Dimensions

Reinforcement learning (RL) algorithms have proven transformative in a range of domains. To tackle real-world domains, these systems often use neural networks to learn policies directly from pixels or other high-dimensional sensory input. By contrast, much theory of RL has focused on discrete state spaces or worst-case analysis, and fundamental questions remain about the dynamics of policy learning in high-dimensional settings. Here, we propose a solvable high-dimensional model of RL that can capture a variety of learning protocols, and derive its typical dynamics as a set of closed-form ordinary differential equations (ODEs). We derive optimal schedules for the learning rates and task difficulty - analogous to annealing schemes and curricula during training in RL - and show that the model exhibits rich behaviour, including delayed learning under sparse rewards; a variety of learning regimes depending on reward baselines; and a speed-accuracy trade-off driven by reward stringency. Experiments on variants of the Procgen game "Bossfight" and Arcade Learning Environment game "Pong" also show such a speed-accuracy trade-off in practice. Together, these results take a step towards closing the gap between theory and practice in high-dimensional RL.

Quantifying lottery tickets under label noise: accuracy, calibration, and complexity

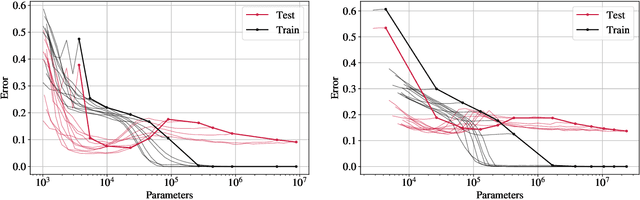
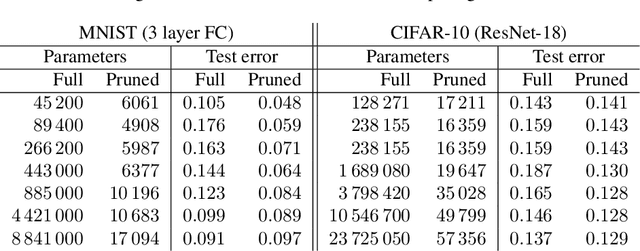
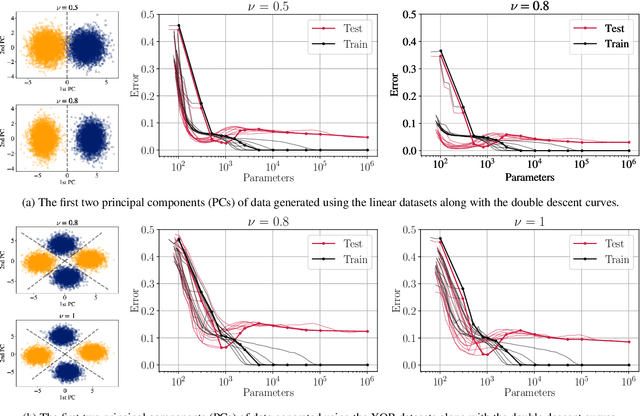
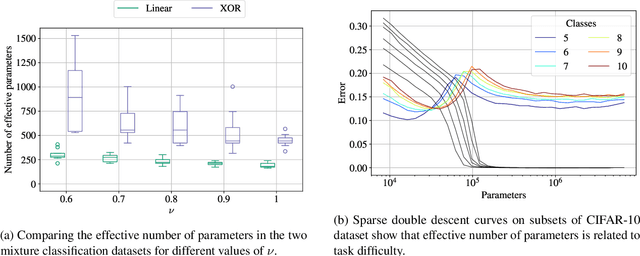
Pruning deep neural networks is a widely used strategy to alleviate the computational burden in machine learning. Overwhelming empirical evidence suggests that pruned models retain very high accuracy even with a tiny fraction of parameters. However, relatively little work has gone into characterising the small pruned networks obtained, beyond a measure of their accuracy. In this paper, we use the sparse double descent approach to identify univocally and characterise pruned models associated with classification tasks. We observe empirically that, for a given task, iterative magnitude pruning (IMP) tends to converge to networks of comparable sizes even when starting from full networks with sizes ranging over orders of magnitude. We analyse the best pruned models in a controlled experimental setup and show that their number of parameters reflects task difficulty and that they are much better than full networks at capturing the true conditional probability distribution of the labels. On real data, we similarly observe that pruned models are less prone to overconfident predictions. Our results suggest that pruned models obtained via IMP not only have advantageous computational properties but also provide a better representation of uncertainty in learning.

Attacks on Online Learners: a Teacher-Student Analysis

Machine learning models are famously vulnerable to adversarial attacks: small ad-hoc perturbations of the data that can catastrophically alter the model predictions. While a large literature has studied the case of test-time attacks on pre-trained models, the important case of attacks in an online learning setting has received little attention so far. In this work, we use a control-theoretical perspective to study the scenario where an attacker may perturb data labels to manipulate the learning dynamics of an online learner. We perform a theoretical analysis of the problem in a teacher-student setup, considering different attack strategies, and obtaining analytical results for the steady state of simple linear learners. These results enable us to prove that a discontinuous transition in the learner's accuracy occurs when the attack strength exceeds a critical threshold. We then study empirically attacks on learners with complex architectures using real data, confirming the insights of our theoretical analysis. Our findings show that greedy attacks can be extremely efficient, especially when data stream in small batches.