Guido Sanguinetti
School of Informatics, University of Edinburgh, SynthSys, Centre for Synthetic and Systems Biology, University of Edinburgh
Cartan Networks: Group theoretical Hyperbolic Deep Learning
May 30, 2025Abstract:Hyperbolic deep learning leverages the metric properties of hyperbolic spaces to develop efficient and informative embeddings of hierarchical data. Here, we focus on the solvable group structure of hyperbolic spaces, which follows naturally from their construction as symmetric spaces. This dual nature of Lie group and Riemannian manifold allows us to propose a new class of hyperbolic deep learning algorithms where group homomorphisms are interleaved with metric-preserving diffeomorphisms. The resulting algorithms, which we call Cartan networks, show promising results on various benchmark data sets and open the way to a novel class of hyperbolic deep learning architectures.
Quantifying lottery tickets under label noise: accuracy, calibration, and complexity
Jun 21, 2023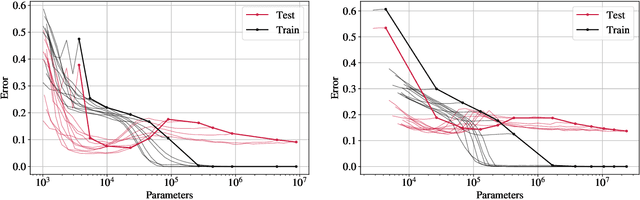
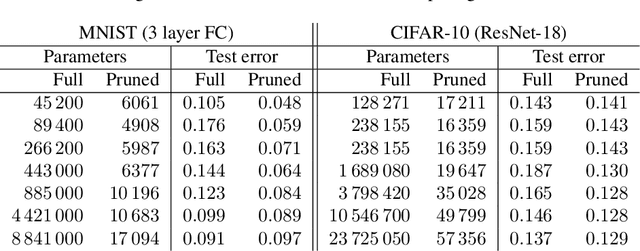
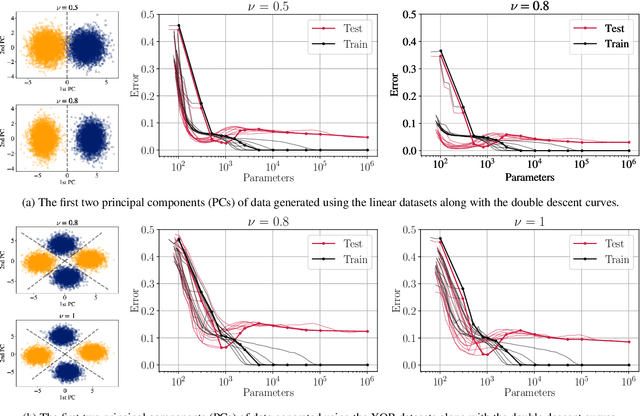
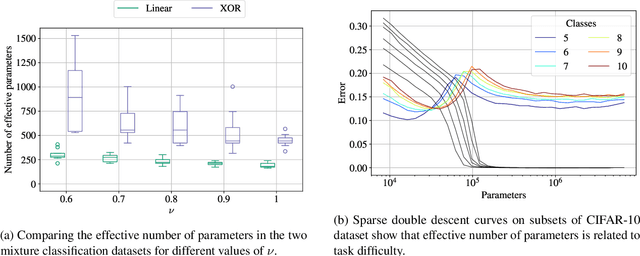
Abstract:Pruning deep neural networks is a widely used strategy to alleviate the computational burden in machine learning. Overwhelming empirical evidence suggests that pruned models retain very high accuracy even with a tiny fraction of parameters. However, relatively little work has gone into characterising the small pruned networks obtained, beyond a measure of their accuracy. In this paper, we use the sparse double descent approach to identify univocally and characterise pruned models associated with classification tasks. We observe empirically that, for a given task, iterative magnitude pruning (IMP) tends to converge to networks of comparable sizes even when starting from full networks with sizes ranging over orders of magnitude. We analyse the best pruned models in a controlled experimental setup and show that their number of parameters reflects task difficulty and that they are much better than full networks at capturing the true conditional probability distribution of the labels. On real data, we similarly observe that pruned models are less prone to overconfident predictions. Our results suggest that pruned models obtained via IMP not only have advantageous computational properties but also provide a better representation of uncertainty in learning.
Attacks on Online Learners: a Teacher-Student Analysis
May 18, 2023Abstract:Machine learning models are famously vulnerable to adversarial attacks: small ad-hoc perturbations of the data that can catastrophically alter the model predictions. While a large literature has studied the case of test-time attacks on pre-trained models, the important case of attacks in an online learning setting has received little attention so far. In this work, we use a control-theoretical perspective to study the scenario where an attacker may perturb data labels to manipulate the learning dynamics of an online learner. We perform a theoretical analysis of the problem in a teacher-student setup, considering different attack strategies, and obtaining analytical results for the steady state of simple linear learners. These results enable us to prove that a discontinuous transition in the learner's accuracy occurs when the attack strength exceeds a critical threshold. We then study empirically attacks on learners with complex architectures using real data, confirming the insights of our theoretical analysis. Our findings show that greedy attacks can be extremely efficient, especially when data stream in small batches.
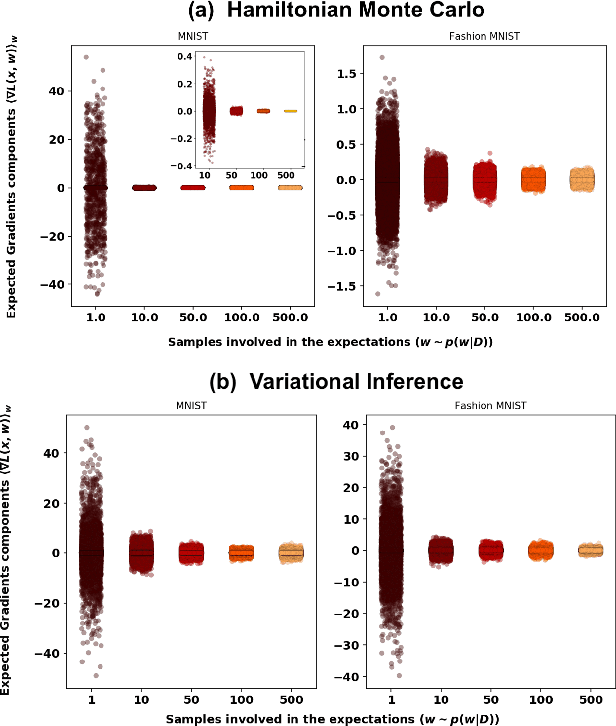
On the Robustness of Bayesian Neural Networks to Adversarial Attacks
Jul 13, 2022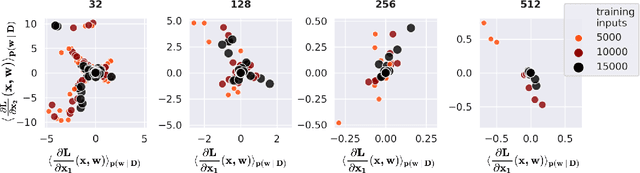
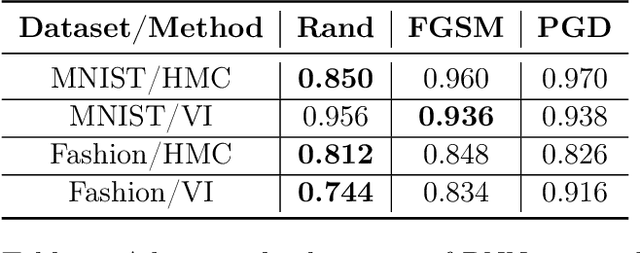
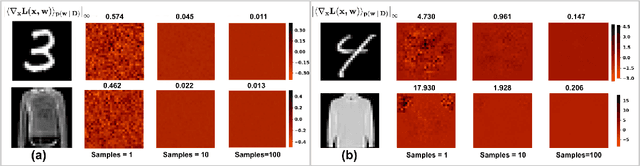
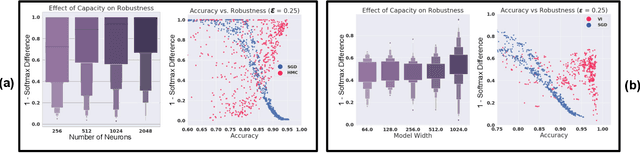
Abstract:Vulnerability to adversarial attacks is one of the principal hurdles to the adoption of deep learning in safety-critical applications. Despite significant efforts, both practical and theoretical, training deep learning models robust to adversarial attacks is still an open problem. In this paper, we analyse the geometry of adversarial attacks in the large-data, overparameterized limit for Bayesian Neural Networks (BNNs). We show that, in the limit, vulnerability to gradient-based attacks arises as a result of degeneracy in the data distribution, i.e., when the data lies on a lower-dimensional submanifold of the ambient space. As a direct consequence, we demonstrate that in this limit BNN posteriors are robust to gradient-based adversarial attacks. Crucially, we prove that the expected gradient of the loss with respect to the BNN posterior distribution is vanishing, even when each neural network sampled from the posterior is vulnerable to gradient-based attacks. Experimental results on the MNIST, Fashion MNIST, and half moons datasets, representing the finite data regime, with BNNs trained with Hamiltonian Monte Carlo and Variational Inference, support this line of arguments, showing that BNNs can display both high accuracy on clean data and robustness to both gradient-based and gradient-free based adversarial attacks.
Resilience of Bayesian Layer-Wise Explanations under Adversarial Attacks
Feb 22, 2021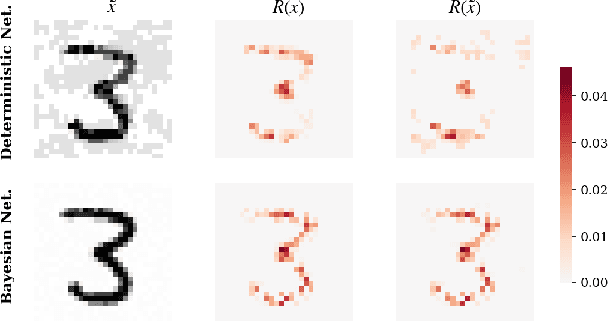

Abstract:We consider the problem of the stability of saliency-based explanations of Neural Network predictions under adversarial attacks in a classification task. We empirically show that, for deterministic Neural Networks, saliency interpretations are remarkably brittle even when the attacks fail, i.e. for attacks that do not change the classification label. By leveraging recent results, we provide a theoretical explanation of this result in terms of the geometry of adversarial attacks. Based on these theoretical considerations, we suggest and demonstrate empirically that saliency explanations provided by Bayesian Neural Networks are considerably more stable under adversarial perturbations. Our results not only confirm that Bayesian Neural Networks are more robust to adversarial attacks, but also demonstrate that Bayesian methods have the potential to provide more stable and interpretable assessments of Neural Network predictions.
Random Projections for Improved Adversarial Robustness
Feb 18, 2021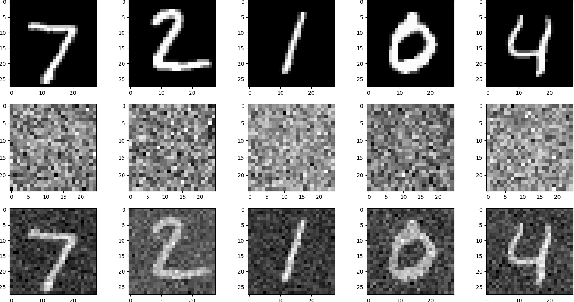
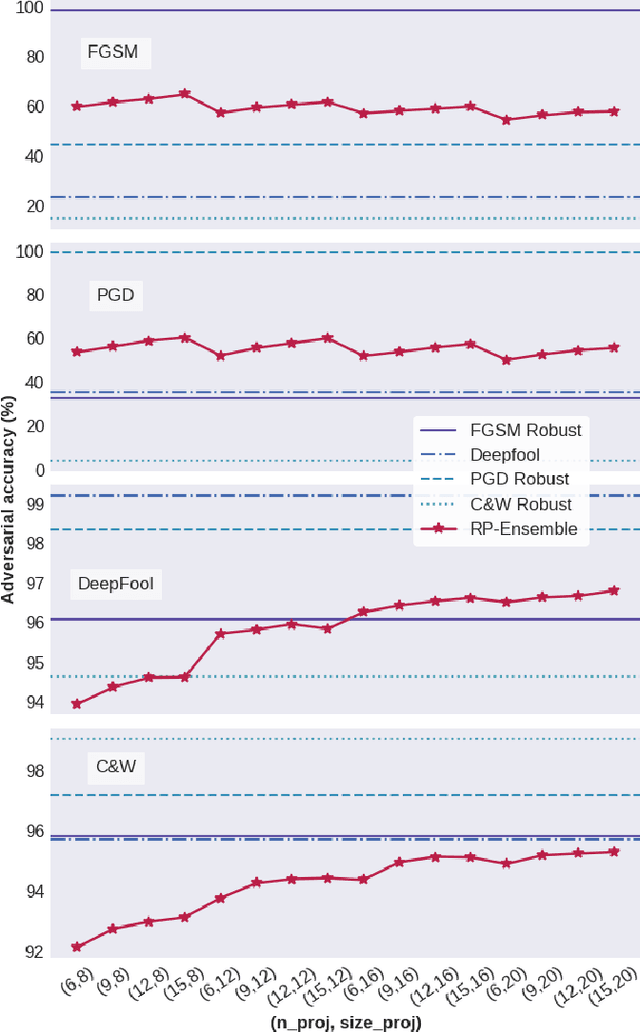
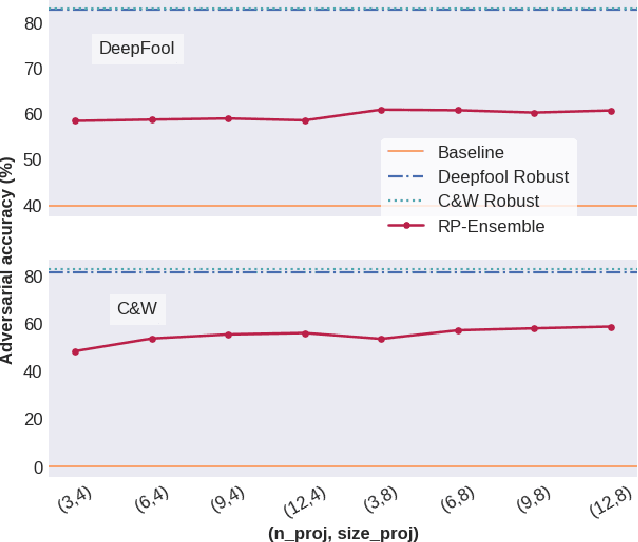

Abstract:We propose two training techniques for improving the robustness of Neural Networks to adversarial attacks, i.e. manipulations of the inputs that are maliciously crafted to fool networks into incorrect predictions. Both methods are independent of the chosen attack and leverage random projections of the original inputs, with the purpose of exploiting both dimensionality reduction and some characteristic geometrical properties of adversarial perturbations. The first technique is called RP-Ensemble and consists of an ensemble of networks trained on multiple projected versions of the original inputs. The second one, named RP-Regularizer, adds instead a regularization term to the training objective.
Robustness of Bayesian Neural Networks to Gradient-Based Attacks
Feb 12, 2020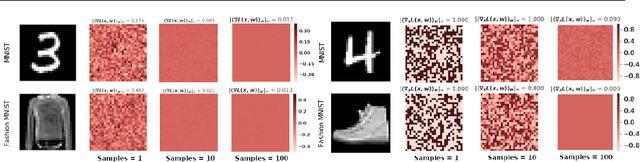
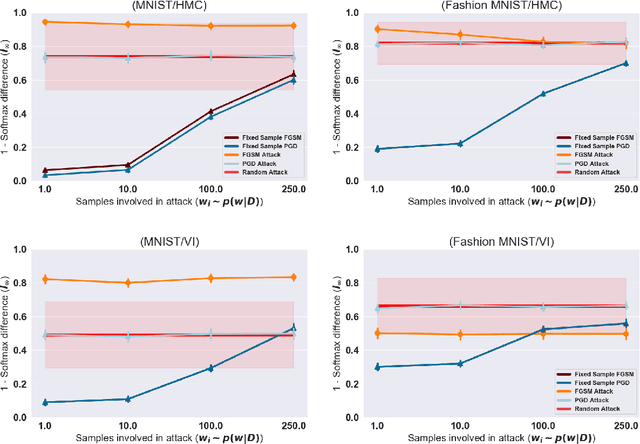
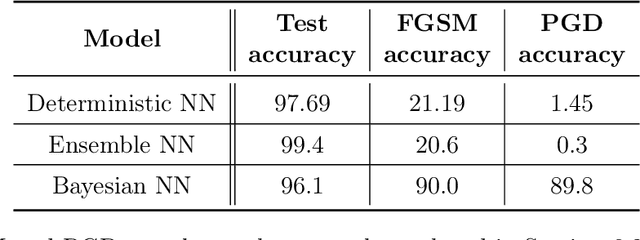
Abstract:Vulnerability to adversarial attacks is one of the principal hurdles to the adoption of deep learning in safety-critical applications. Despite significant efforts, both practical and theoretical, the problem remains open. In this paper, we analyse the geometry of adversarial attacks in the large-data, overparametrized limit for Bayesian Neural Networks (BNNs). We show that, in the limit, vulnerability to gradient-based attacks arises as a result of degeneracy in the data distribution, i.e., when the data lies on a lower-dimensional submanifold of the ambient space. As a direct consequence, we demonstrate that in the limit BNN posteriors are robust to gradient-based adversarial attacks. Experimental results on the MNIST and Fashion MNIST datasets with BNNs trained with Hamiltonian Monte Carlo and Variational Inference support this line of argument, showing that BNNs can display both high accuracy and robustness to gradient based adversarial attacks.
Geometric fluid approximation for general continuous-time Markov chains
Jan 31, 2019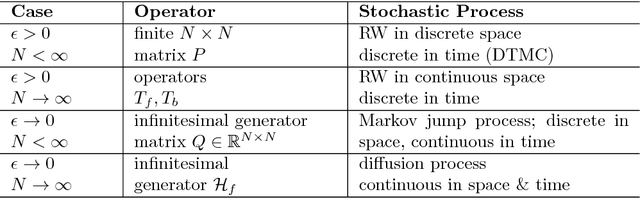

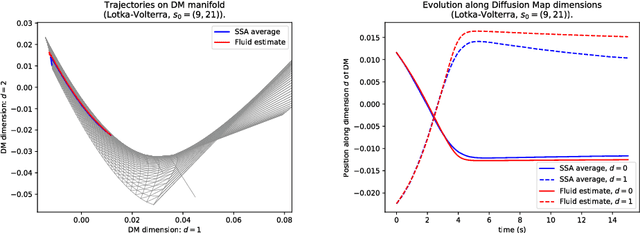
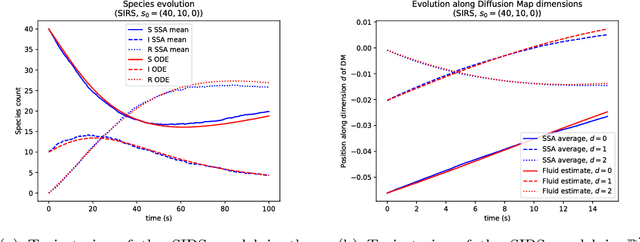
Abstract:Fluid approximations have seen great success in approximating the macro-scale behaviour of Markov systems with a large number of discrete states. However, these methods rely on the continuous-time Markov chain (CTMC) having a particular population structure which suggests a natural continuous state-space endowed with a dynamics for the approximating process. We construct here a general method based on spectral analysis of the transition matrix of the CTMC, without the need for a population structure. Specifically, we use the popular manifold learning method of diffusion maps to analyse the transition matrix as the operator of a hidden continuous process. An embedding of states in a continuous space is recovered, and the space is endowed with a drift vector field inferred via Gaussian process regression. In this manner, we construct an ODE whose solution approximates the evolution of the CTMC mean, mapped onto the continuous space (known as the fluid limit).
Intrinsic Geometric Vulnerability of High-Dimensional Artificial Intelligence
Nov 08, 2018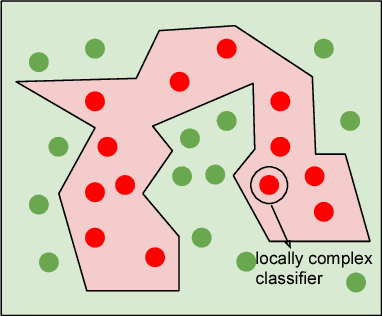
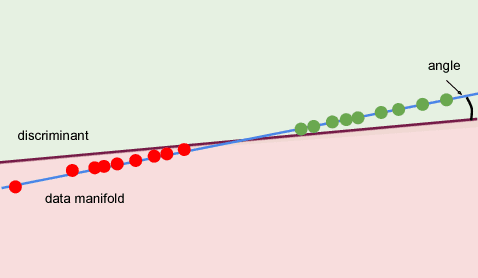
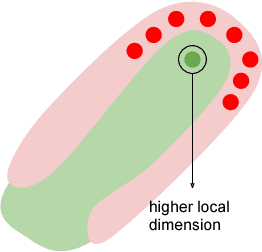
Abstract:The success of modern Artificial Intelligence (AI) technologies depends critically on the ability to learn non-linear functional dependencies from large, high dimensional data sets. Despite recent high-profile successes, empirical evidence indicates that the high predictive performance is often paired with low robustness, making AI systems potentially vulnerable to adversarial attacks. In this report, we provide a simple intuitive argument suggesting that high performance and vulnerability are intrinsically coupled, and largely dependent on the geometry of typical, high-dimensional data sets. Our work highlights a major potential pitfall of modern AI systems, and suggests practical research directions to ameliorate the problem.
Efficient Low-Order Approximation of First-Passage Time Distributions
Nov 01, 2017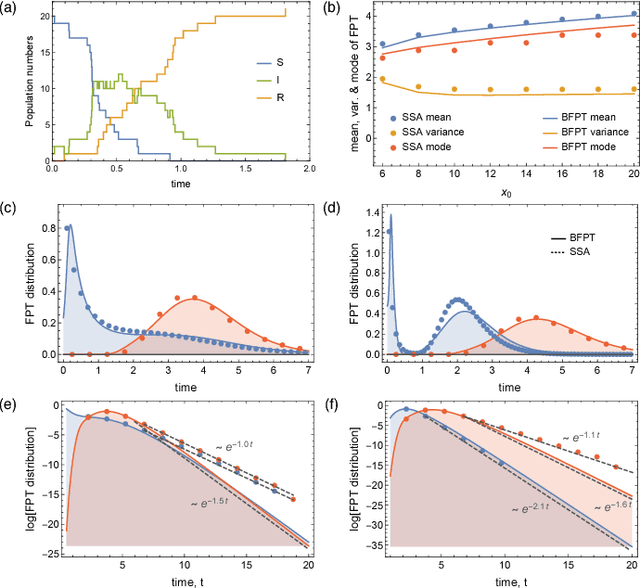

Abstract:We consider the problem of computing first-passage time distributions for reaction processes modelled by master equations. We show that this generally intractable class of problems is equivalent to a sequential Bayesian inference problem for an auxiliary observation process. The solution can be approximated efficiently by solving a closed set of coupled ordinary differential equations (for the low-order moments of the process) whose size scales with the number of species. We apply it to an epidemic model and a trimerisation process, and show good agreement with stochastic simulations.
* 5 pages, 3 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge