Stochastic Weight Sharing for Bayesian Neural Networks

While offering a principled framework for uncertainty quantification in deep learning, the employment of Bayesian Neural Networks (BNNs) is still constrained by their increased computational requirements and the convergence difficulties when training very deep, state-of-the-art architectures. In this work, we reinterpret weight-sharing quantization techniques from a stochastic perspective in the context of training and inference with Bayesian Neural Networks (BNNs). Specifically, we leverage 2D adaptive Gaussian distributions, Wasserstein distance estimations, and alpha blending to encode the stochastic behaviour of a BNN in a lower dimensional, soft Gaussian representation. Through extensive empirical investigation, we demonstrate that our approach significantly reduces the computational overhead inherent in Bayesian learning by several orders of magnitude, enabling the efficient Bayesian training of large-scale models, such as ResNet-101 and Vision Transformer (VIT). On various computer vision benchmarks including CIFAR10, CIFAR100, and ImageNet1k. Our approach compresses model parameters by approximately 50x and reduces model size by 75, while achieving accuracy and uncertainty estimations comparable to the state-of-the-art.

Probabilistic Reach-Avoid for Bayesian Neural Networks

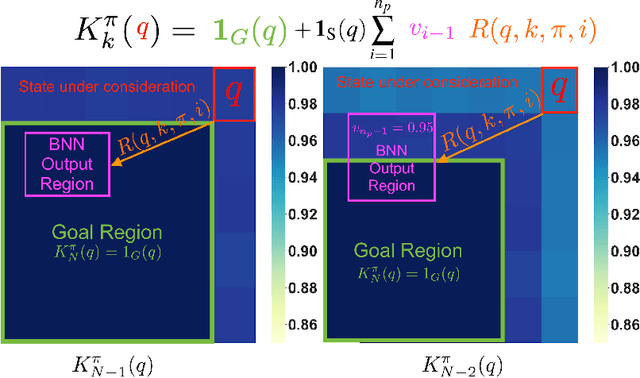
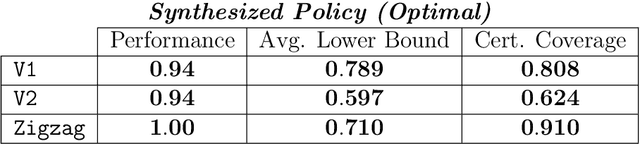
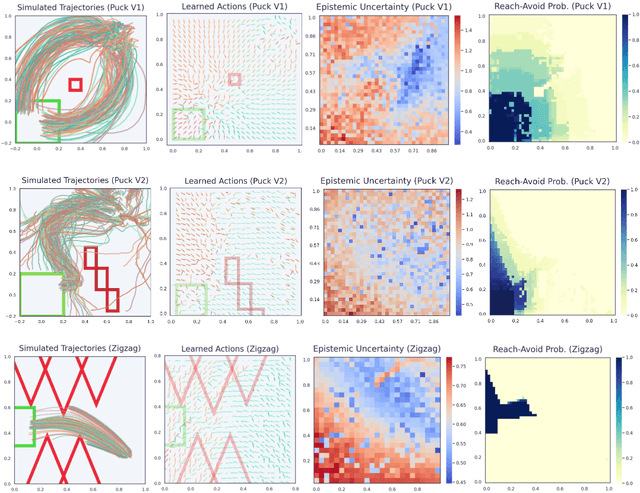
Model-based reinforcement learning seeks to simultaneously learn the dynamics of an unknown stochastic environment and synthesise an optimal policy for acting in it. Ensuring the safety and robustness of sequential decisions made through a policy in such an environment is a key challenge for policies intended for safety-critical scenarios. In this work, we investigate two complementary problems: first, computing reach-avoid probabilities for iterative predictions made with dynamical models, with dynamics described by Bayesian neural network (BNN); second, synthesising control policies that are optimal with respect to a given reach-avoid specification (reaching a "target" state, while avoiding a set of "unsafe" states) and a learned BNN model. Our solution leverages interval propagation and backward recursion techniques to compute lower bounds for the probability that a policy's sequence of actions leads to satisfying the reach-avoid specification. Such computed lower bounds provide safety certification for the given policy and BNN model. We then introduce control synthesis algorithms to derive policies maximizing said lower bounds on the safety probability. We demonstrate the effectiveness of our method on a series of control benchmarks characterized by learned BNN dynamics models. On our most challenging benchmark, compared to purely data-driven policies the optimal synthesis algorithm is able to provide more than a four-fold increase in the number of certifiable states and more than a three-fold increase in the average guaranteed reach-avoid probability.

Adversarial Robustness Certification for Bayesian Neural Networks

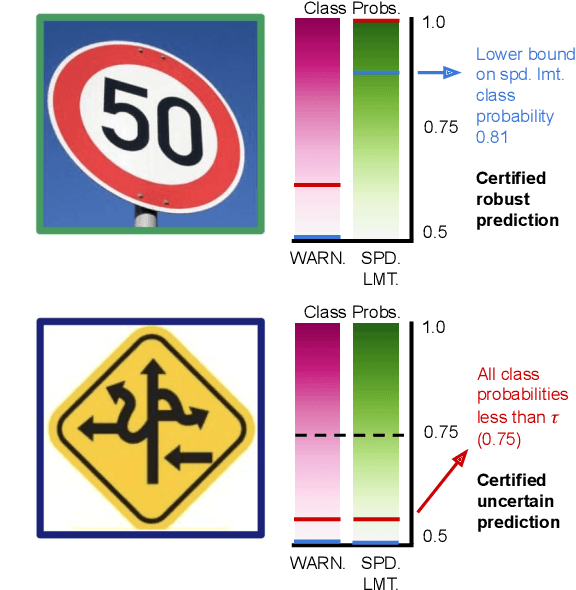
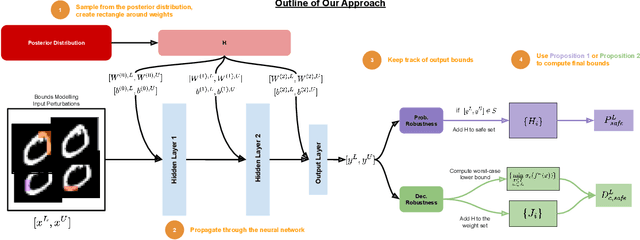
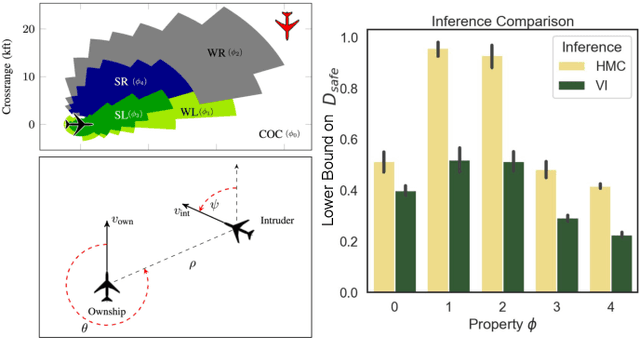
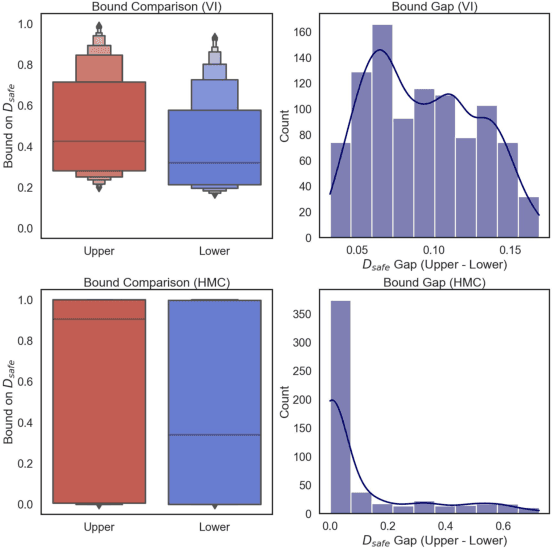
We study the problem of certifying the robustness of Bayesian neural networks (BNNs) to adversarial input perturbations. Given a compact set of input points $T \subseteq \mathbb{R}^m$ and a set of output points $S \subseteq \mathbb{R}^n$, we define two notions of robustness for BNNs in an adversarial setting: probabilistic robustness and decision robustness. Probabilistic robustness is the probability that for all points in $T$ the output of a BNN sampled from the posterior is in $S$. On the other hand, decision robustness considers the optimal decision of a BNN and checks if for all points in $T$ the optimal decision of the BNN for a given loss function lies within the output set $S$. Although exact computation of these robustness properties is challenging due to the probabilistic and non-convex nature of BNNs, we present a unified computational framework for efficiently and formally bounding them. Our approach is based on weight interval sampling, integration, and bound propagation techniques, and can be applied to BNNs with a large number of parameters, and independently of the (approximate) inference method employed to train the BNN. We evaluate the effectiveness of our methods on various regression and classification tasks, including an industrial regression benchmark, MNIST, traffic sign recognition, and airborne collision avoidance, and demonstrate that our approach enables certification of robustness and uncertainty of BNN predictions.

BNN-DP: Robustness Certification of Bayesian Neural Networks via Dynamic Programming

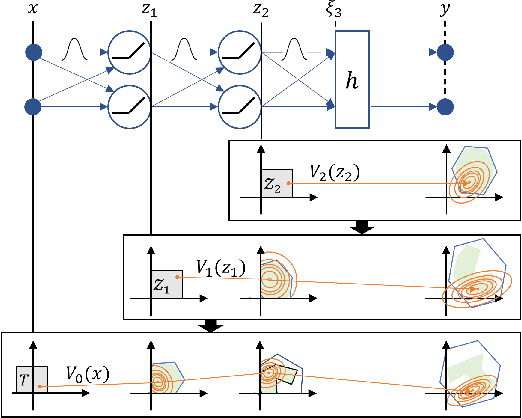
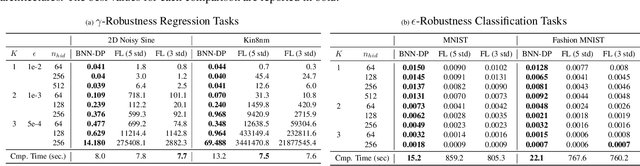
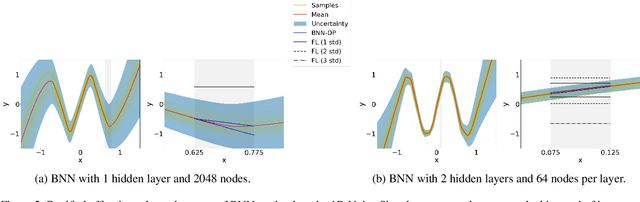
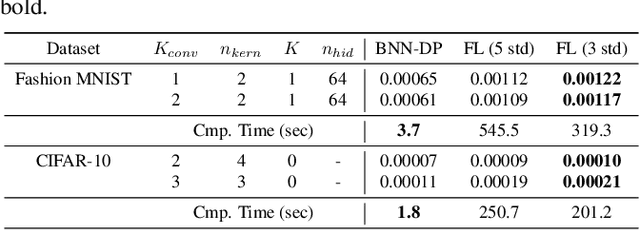
In this paper, we introduce BNN-DP, an efficient algorithmic framework for analysis of adversarial robustness of Bayesian Neural Networks (BNNs). Given a compact set of input points $T\subset \mathbb{R}^n$, BNN-DP computes lower and upper bounds on the BNN's predictions for all the points in $T$. The framework is based on an interpretation of BNNs as stochastic dynamical systems, which enables the use of Dynamic Programming (DP) algorithms to bound the prediction range along the layers of the network. Specifically, the method uses bound propagation techniques and convex relaxations to derive a backward recursion procedure to over-approximate the prediction range of the BNN with piecewise affine functions. The algorithm is general and can handle both regression and classification tasks. On a set of experiments on various regression and classification tasks and BNN architectures, we show that BNN-DP outperforms state-of-the-art methods by up to four orders of magnitude in both tightness of the bounds and computational efficiency.

Individual Fairness in Bayesian Neural Networks

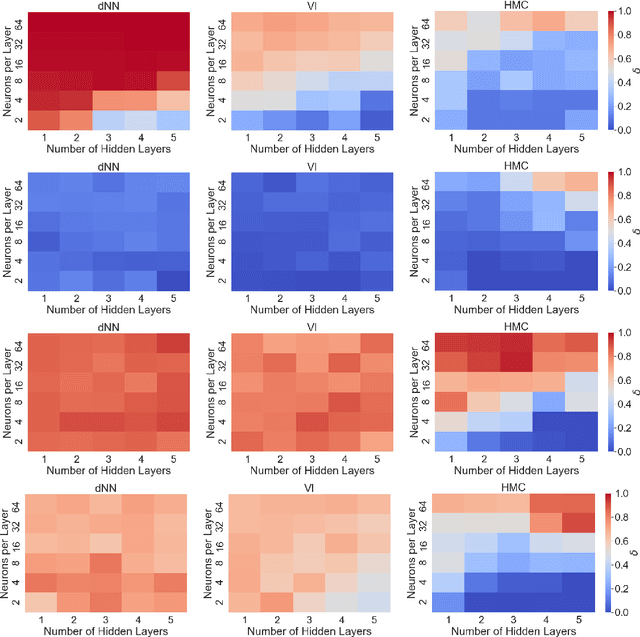
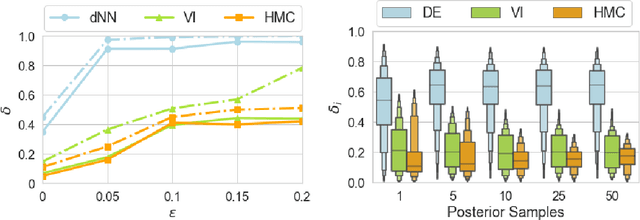
We study Individual Fairness (IF) for Bayesian neural networks (BNNs). Specifically, we consider the $\epsilon$-$\delta$-individual fairness notion, which requires that, for any pair of input points that are $\epsilon$-similar according to a given similarity metrics, the output of the BNN is within a given tolerance $\delta>0.$ We leverage bounds on statistical sampling over the input space and the relationship between adversarial robustness and individual fairness to derive a framework for the systematic estimation of $\epsilon$-$\delta$-IF, designing Fair-FGSM and Fair-PGD as global,fairness-aware extensions to gradient-based attacks for BNNs. We empirically study IF of a variety of approximately inferred BNNs with different architectures on fairness benchmarks, and compare against deterministic models learnt using frequentist techniques. Interestingly, we find that BNNs trained by means of approximate Bayesian inference consistently tend to be markedly more individually fair than their deterministic counterparts.

On the Robustness of Bayesian Neural Networks to Adversarial Attacks

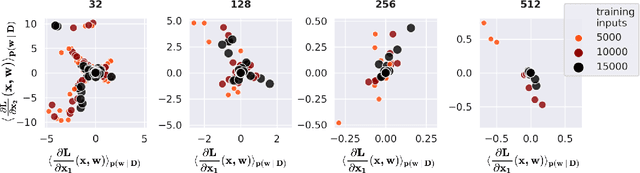
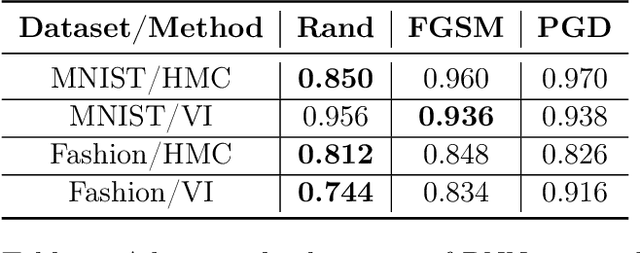
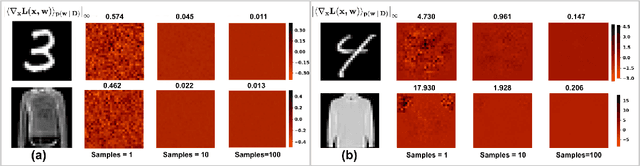
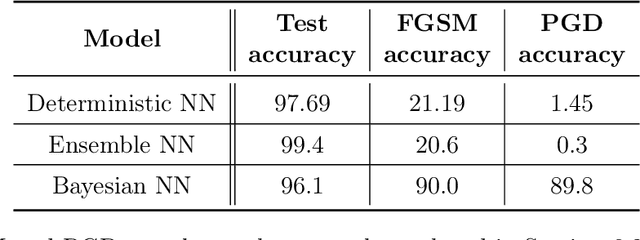
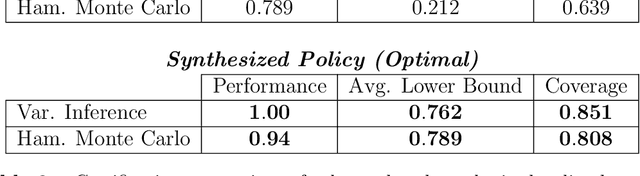
Vulnerability to adversarial attacks is one of the principal hurdles to the adoption of deep learning in safety-critical applications. Despite significant efforts, both practical and theoretical, training deep learning models robust to adversarial attacks is still an open problem. In this paper, we analyse the geometry of adversarial attacks in the large-data, overparameterized limit for Bayesian Neural Networks (BNNs). We show that, in the limit, vulnerability to gradient-based attacks arises as a result of degeneracy in the data distribution, i.e., when the data lies on a lower-dimensional submanifold of the ambient space. As a direct consequence, we demonstrate that in this limit BNN posteriors are robust to gradient-based adversarial attacks. Crucially, we prove that the expected gradient of the loss with respect to the BNN posterior distribution is vanishing, even when each neural network sampled from the posterior is vulnerable to gradient-based attacks. Experimental results on the MNIST, Fashion MNIST, and half moons datasets, representing the finite data regime, with BNNs trained with Hamiltonian Monte Carlo and Variational Inference, support this line of arguments, showing that BNNs can display both high accuracy on clean data and robustness to both gradient-based and gradient-free based adversarial attacks.

Individual Fairness Guarantees for Neural Networks

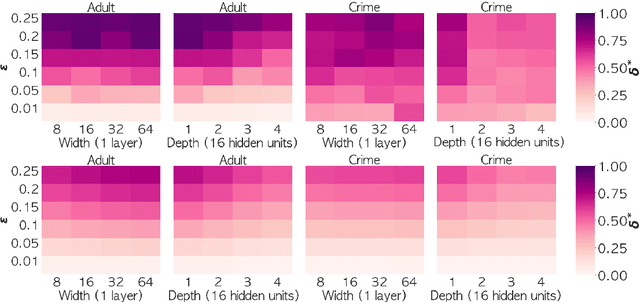
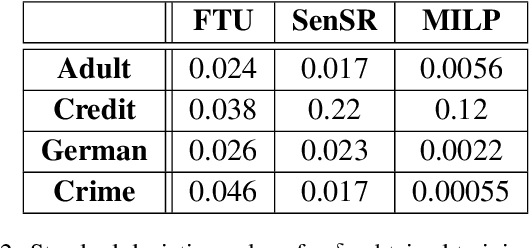
We consider the problem of certifying the individual fairness (IF) of feed-forward neural networks (NNs). In particular, we work with the $\epsilon$-$\delta$-IF formulation, which, given a NN and a similarity metric learnt from data, requires that the output difference between any pair of $\epsilon$-similar individuals is bounded by a maximum decision tolerance $\delta \geq 0$. Working with a range of metrics, including the Mahalanobis distance, we propose a method to overapproximate the resulting optimisation problem using piecewise-linear functions to lower and upper bound the NN's non-linearities globally over the input space. We encode this computation as the solution of a Mixed-Integer Linear Programming problem and demonstrate that it can be used to compute IF guarantees on four datasets widely used for fairness benchmarking. We show how this formulation can be used to encourage models' fairness at training time by modifying the NN loss, and empirically confirm our approach yields NNs that are orders of magnitude fairer than state-of-the-art methods.

Certification of Iterative Predictions in Bayesian Neural Networks

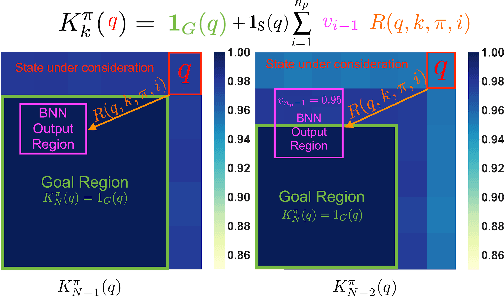
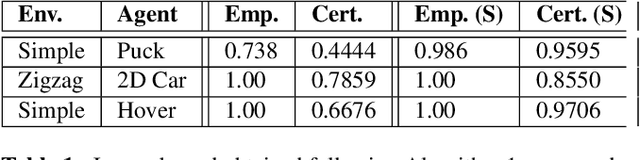
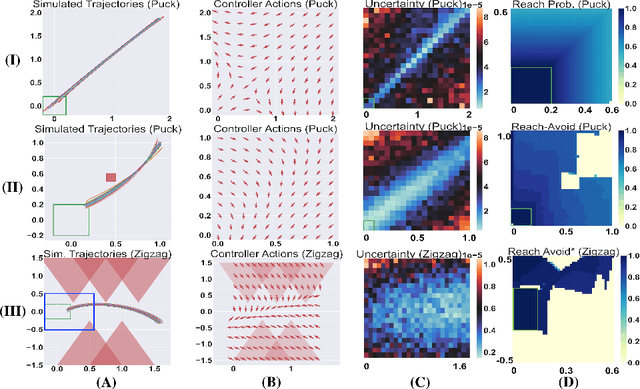
We consider the problem of computing reach-avoid probabilities for iterative predictions made with Bayesian neural network (BNN) models. Specifically, we leverage bound propagation techniques and backward recursion to compute lower bounds for the probability that trajectories of the BNN model reach a given set of states while avoiding a set of unsafe states. We use the lower bounds in the context of control and reinforcement learning to provide safety certification for given control policies, as well as to synthesize control policies that improve the certification bounds. On a set of benchmarks, we demonstrate that our framework can be employed to certify policies over BNNs predictions for problems of more than $10$ dimensions, and to effectively synthesize policies that significantly increase the lower bound on the satisfaction probability.

Adversarial Robustness Guarantees for Gaussian Processes

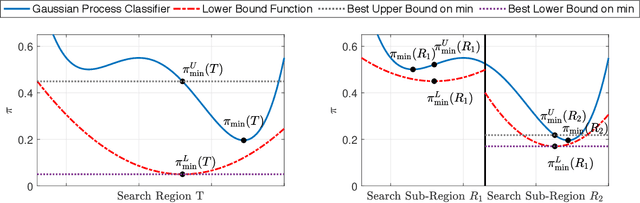
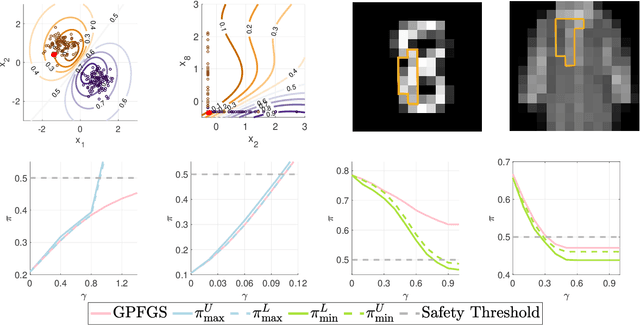
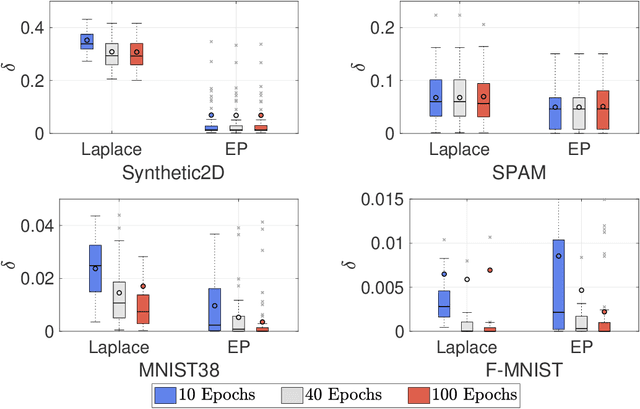
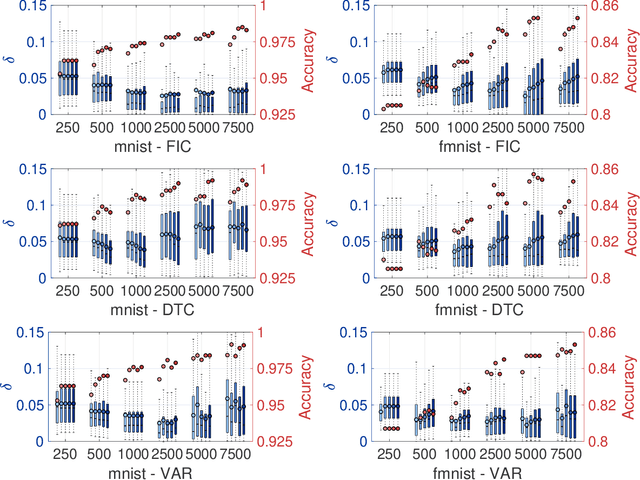
Gaussian processes (GPs) enable principled computation of model uncertainty, making them attractive for safety-critical applications. Such scenarios demand that GP decisions are not only accurate, but also robust to perturbations. In this paper we present a framework to analyse adversarial robustness of GPs, defined as invariance of the model's decision to bounded perturbations. Given a compact subset of the input space $T\subseteq \mathbb{R}^d$, a point $x^*$ and a GP, we provide provable guarantees of adversarial robustness of the GP by computing lower and upper bounds on its prediction range in $T$. We develop a branch-and-bound scheme to refine the bounds and show, for any $\epsilon > 0$, that our algorithm is guaranteed to converge to values $\epsilon$-close to the actual values in finitely many iterations. The algorithm is anytime and can handle both regression and classification tasks, with analytical formulation for most kernels used in practice. We evaluate our methods on a collection of synthetic and standard benchmark datasets, including SPAM, MNIST and FashionMNIST. We study the effect of approximate inference techniques on robustness and demonstrate how our method can be used for interpretability. Our empirical results suggest that the adversarial robustness of GPs increases with accurate posterior estimation.

Bayesian Inference with Certifiable Adversarial Robustness

We consider adversarial training of deep neural networks through the lens of Bayesian learning, and present a principled framework for adversarial training of Bayesian Neural Networks (BNNs) with certifiable guarantees. We rely on techniques from constraint relaxation of non-convex optimisation problems and modify the standard cross-entropy error model to enforce posterior robustness to worst-case perturbations in $\epsilon$-balls around input points. We illustrate how the resulting framework can be combined with methods commonly employed for approximate inference of BNNs. In an empirical investigation, we demonstrate that the presented approach enables training of certifiably robust models on MNIST, FashionMNIST and CIFAR-10 and can also be beneficial for uncertainty calibration. Our method is the first to directly train certifiable BNNs, thus facilitating their deployment in safety-critical applications.