Individual Fairness Guarantees for Neural Networks
Paper and Code
May 11, 2022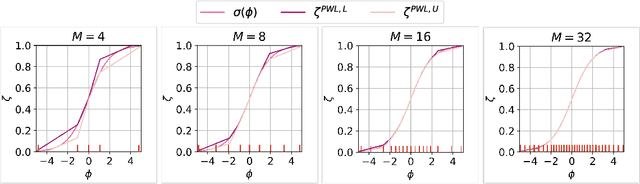
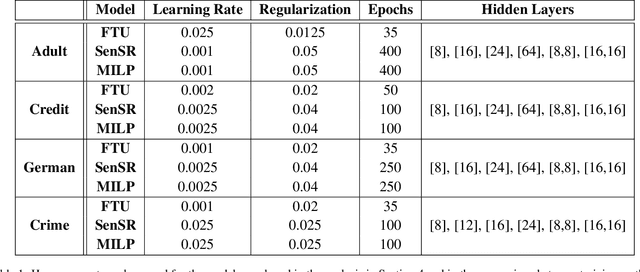
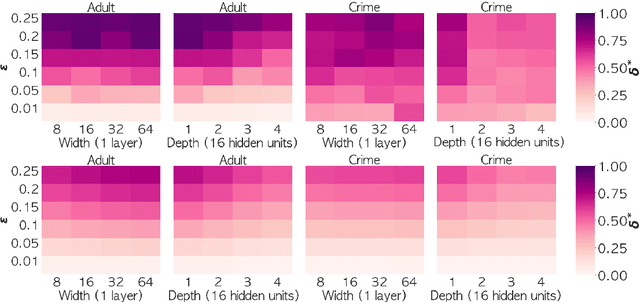
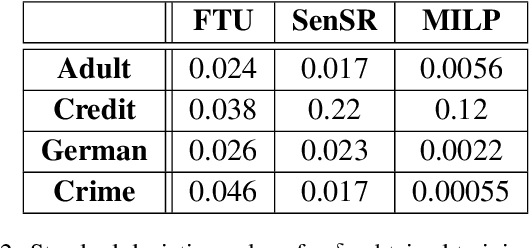
We consider the problem of certifying the individual fairness (IF) of feed-forward neural networks (NNs). In particular, we work with the $\epsilon$-$\delta$-IF formulation, which, given a NN and a similarity metric learnt from data, requires that the output difference between any pair of $\epsilon$-similar individuals is bounded by a maximum decision tolerance $\delta \geq 0$. Working with a range of metrics, including the Mahalanobis distance, we propose a method to overapproximate the resulting optimisation problem using piecewise-linear functions to lower and upper bound the NN's non-linearities globally over the input space. We encode this computation as the solution of a Mixed-Integer Linear Programming problem and demonstrate that it can be used to compute IF guarantees on four datasets widely used for fairness benchmarking. We show how this formulation can be used to encourage models' fairness at training time by modifying the NN loss, and empirically confirm our approach yields NNs that are orders of magnitude fairer than state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge