Adversarial Robustness Guarantees for Gaussian Processes

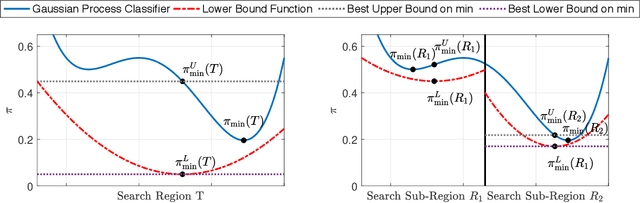
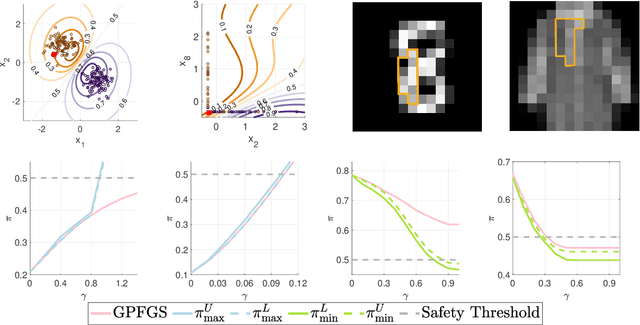
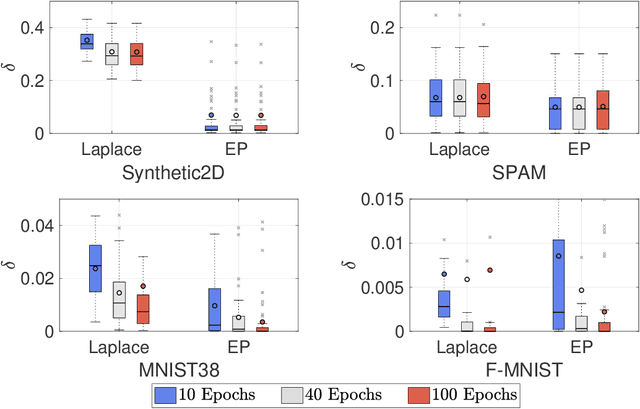
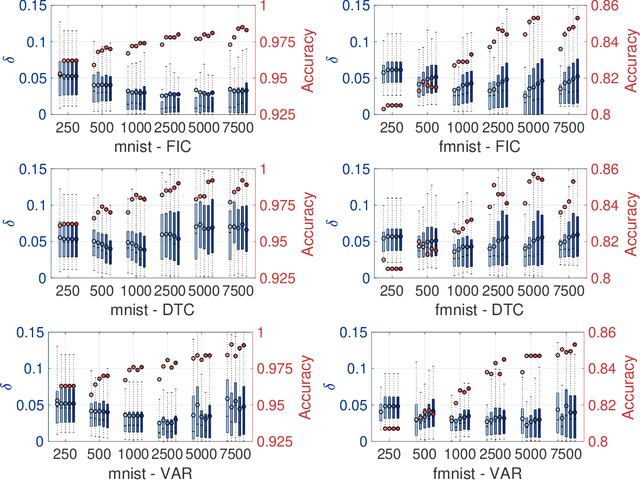
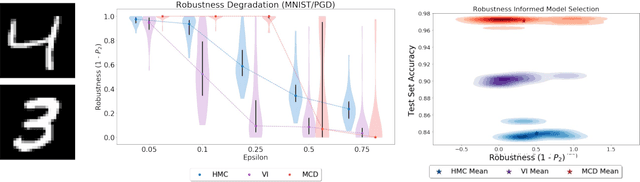
Gaussian processes (GPs) enable principled computation of model uncertainty, making them attractive for safety-critical applications. Such scenarios demand that GP decisions are not only accurate, but also robust to perturbations. In this paper we present a framework to analyse adversarial robustness of GPs, defined as invariance of the model's decision to bounded perturbations. Given a compact subset of the input space $T\subseteq \mathbb{R}^d$, a point $x^*$ and a GP, we provide provable guarantees of adversarial robustness of the GP by computing lower and upper bounds on its prediction range in $T$. We develop a branch-and-bound scheme to refine the bounds and show, for any $\epsilon > 0$, that our algorithm is guaranteed to converge to values $\epsilon$-close to the actual values in finitely many iterations. The algorithm is anytime and can handle both regression and classification tasks, with analytical formulation for most kernels used in practice. We evaluate our methods on a collection of synthetic and standard benchmark datasets, including SPAM, MNIST and FashionMNIST. We study the effect of approximate inference techniques on robustness and demonstrate how our method can be used for interpretability. Our empirical results suggest that the adversarial robustness of GPs increases with accurate posterior estimation.

Safety Guarantees for Planning Based on Iterative Gaussian Processes

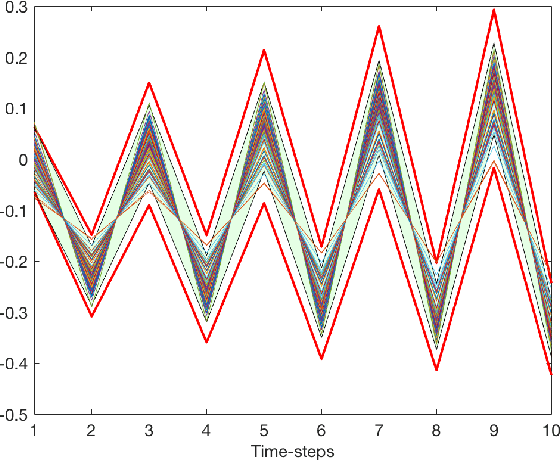
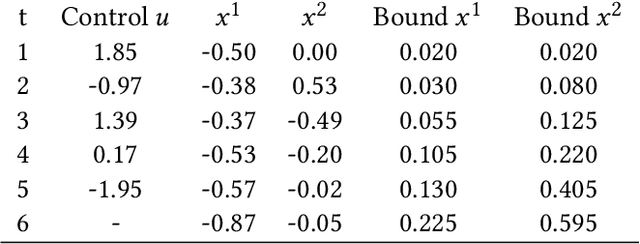
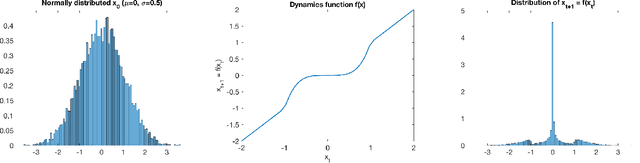
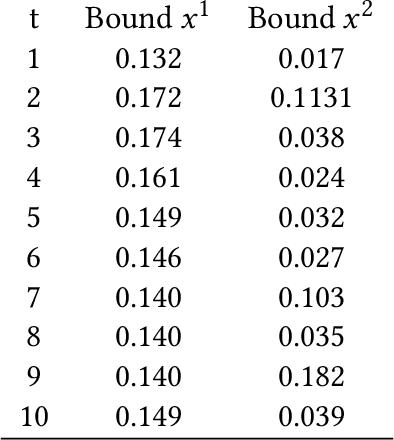
Gaussian Processes (GPs) are widely employed in control and learning because of their principled treatment of uncertainty. However, tracking uncertainty for iterative, multi-step predictions in general leads to an analytically intractable problem. While approximation methods exist, they do not come with guarantees, making it difficult to estimate their reliability and to trust their predictions. In this work, we derive formal probability error bounds for iterative prediction and planning with GPs. Building on GP properties, we bound the probability that random trajectories lie in specific regions around the predicted values. Namely, given a tolerance $\epsilon > 0 $, we compute regions around the predicted trajectory values, such that GP trajectories are guaranteed to lie inside them with probability at least $1-\epsilon$. We verify experimentally that our method tracks the predictive uncertainty correctly, even when current approximation techniques fail. Furthermore, we show how the proposed bounds can be employed within a safe reinforcement learning framework to verify the safety of candidate control policies, guiding the synthesis of provably safe controllers.

Uncertainty Quantification with Statistical Guarantees in End-to-End Autonomous Driving Control

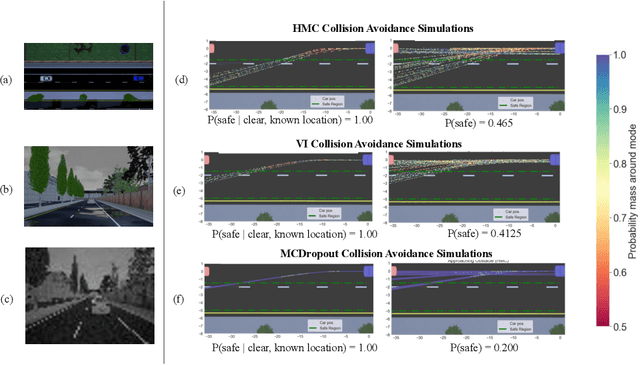
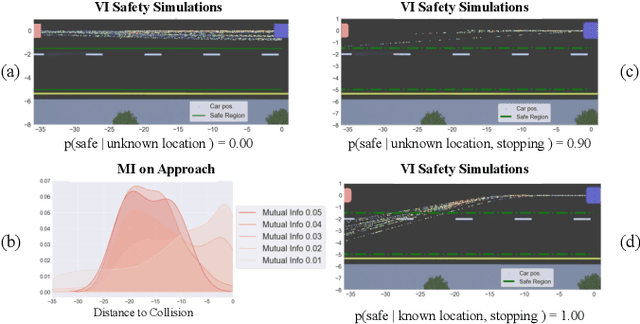
Deep neural network controllers for autonomous driving have recently benefited from significant performance improvements, and have begun deployment in the real world. Prior to their widespread adoption, safety guarantees are needed on the controller behaviour that properly take account of the uncertainty within the model as well as sensor noise. Bayesian neural networks, which assume a prior over the weights, have been shown capable of producing such uncertainty measures, but properties surrounding their safety have not yet been quantified for use in autonomous driving scenarios. In this paper, we develop a framework based on a state-of-the-art simulator for evaluating end-to-end Bayesian controllers. In addition to computing pointwise uncertainty measures that can be computed in real time and with statistical guarantees, we also provide a method for estimating the probability that, given a scenario, the controller keeps the car safe within a finite horizon. We experimentally evaluate the quality of uncertainty computation by several Bayesian inference methods in different scenarios and show how the uncertainty measures can be combined and calibrated for use in collision avoidance. Our results suggest that uncertainty estimates can greatly aid decision making in autonomous driving.

Robustness Quantification for Classification with Gaussian Processes

We consider Bayesian classification with Gaussian processes (GPs) and define robustness of a classifier in terms of the worst-case difference in the classification probabilities with respect to input perturbations. For a subset of the input space $T\subseteq \mathbb{R}^m$ such properties reduce to computing the infimum and supremum of the classification probabilities for all points in $T$. Unfortunately, computing the above values is very challenging, as the classification probabilities cannot be expressed analytically. Nevertheless, using the theory of Gaussian processes, we develop a framework that, for a given dataset $\mathcal{D}$, a compact set of input points $T\subseteq \mathbb{R}^m$ and an error threshold $\epsilon>0$, computes lower and upper bounds of the classification probabilities by over-approximating the exact range with an error bounded by $\epsilon$. We provide experimental comparison of several approximate inference methods for classification on tasks associated to MNIST and SPAM datasets showing that our results enable quantification of uncertainty in adversarial classification settings.

Statistical Guarantees for the Robustness of Bayesian Neural Networks

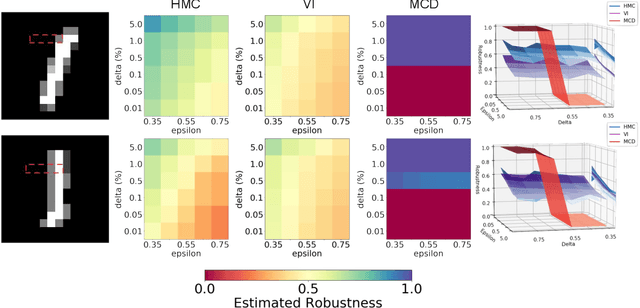
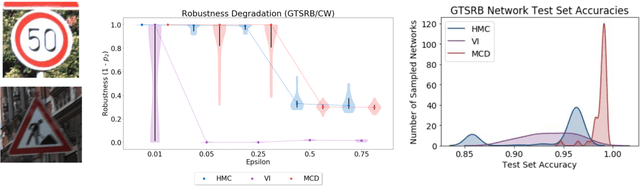
We introduce a probabilistic robustness measure for Bayesian Neural Networks (BNNs), defined as the probability that, given a test point, there exists a point within a bounded set such that the BNN prediction differs between the two. Such a measure can be used, for instance, to quantify the probability of the existence of adversarial examples. Building on statistical verification techniques for probabilistic models, we develop a framework that allows us to estimate probabilistic robustness for a BNN with statistical guarantees, i.e., with a priori error and confidence bounds. We provide experimental comparison for several approximate BNN inference techniques on image classification tasks associated to MNIST and a two-class subset of the GTSRB dataset. Our results enable quantification of uncertainty of BNN predictions in adversarial settings.

Robustness Guarantees for Bayesian Inference with Gaussian Processes

Bayesian inference and Gaussian processes are widely used in applications ranging from robotics and control to biological systems. Many of these applications are safety-critical and require a characterization of the uncertainty associated with the learning model and formal guarantees on its predictions. In this paper we define a robustness measure for Bayesian inference against input perturbations, given by the probability that, for a test point and a compact set in the input space containing the test point, the prediction of the learning model will remain $\delta-$close for all the points in the set, for $\delta>0.$ Such measures can be used to provide formal guarantees for the absence of adversarial examples. By employing the theory of Gaussian processes, we derive tight upper bounds on the resulting robustness by utilising the Borell-TIS inequality, and propose algorithms for their computation. We evaluate our techniques on two examples, a GP regression problem and a fully-connected deep neural network, where we rely on weak convergence to GPs to study adversarial examples on the MNIST dataset.