Physics-Informed Neural Operators for Cardiac Electrophysiology

Accurately simulating systems governed by PDEs, such as voltage fields in cardiac electrophysiology (EP) modelling, remains a significant modelling challenge. Traditional numerical solvers are computationally expensive and sensitive to discretisation, while canonical deep learning methods are data-hungry and struggle with chaotic dynamics and long-term predictions. Physics-Informed Neural Networks (PINNs) mitigate some of these issues by incorporating physical constraints in the learning process, yet they remain limited by mesh resolution and long-term predictive stability. In this work, we propose a Physics-Informed Neural Operator (PINO) approach to solve PDE problems in cardiac EP. Unlike PINNs, PINO models learn mappings between function spaces, allowing them to generalise to multiple mesh resolutions and initial conditions. Our results show that PINO models can accurately reproduce cardiac EP dynamics over extended time horizons and across multiple propagation scenarios, including zero-shot evaluations on scenarios unseen during training. Additionally, our PINO models maintain high predictive quality in long roll-outs (where predictions are recursively fed back as inputs), and can scale their predictive resolution by up to 10x the training resolution. These advantages come with a significant reduction in simulation time compared to numerical PDE solvers, highlighting the potential of PINO-based approaches for efficient and scalable cardiac EP simulations.

DRMD: Deep Reinforcement Learning for Malware Detection under Concept Drift

Malware detection in real-world settings must deal with evolving threats, limited labeling budgets, and uncertain predictions. Traditional classifiers, without additional mechanisms, struggle to maintain performance under concept drift in malware domains, as their supervised learning formulation cannot optimize when to defer decisions to manual labeling and adaptation. Modern malware detection pipelines combine classifiers with monthly active learning (AL) and rejection mechanisms to mitigate the impact of concept drift. In this work, we develop a novel formulation of malware detection as a one-step Markov Decision Process and train a deep reinforcement learning (DRL) agent, simultaneously optimizing sample classification performance and rejecting high-risk samples for manual labeling. We evaluated the joint detection and drift mitigation policy learned by the DRL-based Malware Detection (DRMD) agent through time-aware evaluations on Android malware datasets subject to realistic drift requiring multi-year performance stability. The policies learned under these conditions achieve a higher Area Under Time (AUT) performance compared to standard classification approaches used in the domain, showing improved resilience to concept drift. Specifically, the DRMD agent achieved a $5.18\pm5.44$, $14.49\pm12.86$, and $10.06\pm10.81$ average AUT performance improvement for the classification only, classification with rejection, and classification with rejection and AL settings, respectively. Our results demonstrate for the first time that DRL can facilitate effective malware detection and improved resiliency to concept drift in the dynamic environment of the Android malware domain.

LTL Verification of Memoryful Neural Agents

We present a framework for verifying Memoryful Neural Multi-Agent Systems (MN-MAS) against full Linear Temporal Logic (LTL) specifications. In MN-MAS, agents interact with a non-deterministic, partially observable environment. Examples of MN-MAS include multi-agent systems based on feed-forward and recurrent neural networks or state-space models. Different from previous approaches, we support the verification of both bounded and unbounded LTL specifications. We leverage well-established bounded model checking techniques, including lasso search and invariant synthesis, to reduce the verification problem to that of constraint solving. To solve these constraints, we develop efficient methods based on bound propagation, mixed-integer linear programming, and adaptive splitting. We evaluate the effectiveness of our algorithms in single and multi-agent environments from the Gymnasium and PettingZoo libraries, verifying unbounded specifications for the first time and improving the verification time for bounded specifications by an order of magnitude compared to the SoA.

Robust Counterfactual Inference in Markov Decision Processes

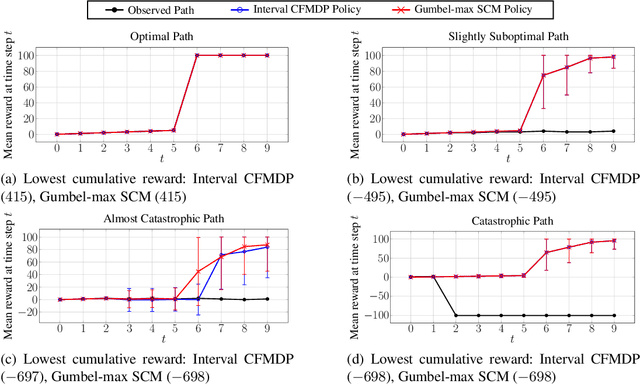
This paper addresses a key limitation in existing counterfactual inference methods for Markov Decision Processes (MDPs). Current approaches assume a specific causal model to make counterfactuals identifiable. However, there are usually many causal models that align with the observational and interventional distributions of an MDP, each yielding different counterfactual distributions, so fixing a particular causal model limits the validity (and usefulness) of counterfactual inference. We propose a novel non-parametric approach that computes tight bounds on counterfactual transition probabilities across all compatible causal models. Unlike previous methods that require solving prohibitively large optimisation problems (with variables that grow exponentially in the size of the MDP), our approach provides closed-form expressions for these bounds, making computation highly efficient and scalable for non-trivial MDPs. Once such an interval counterfactual MDP is constructed, our method identifies robust counterfactual policies that optimise the worst-case reward w.r.t. the uncertain interval MDP probabilities. We evaluate our method on various case studies, demonstrating improved robustness over existing methods.

Distilling Calibration via Conformalized Credal Inference

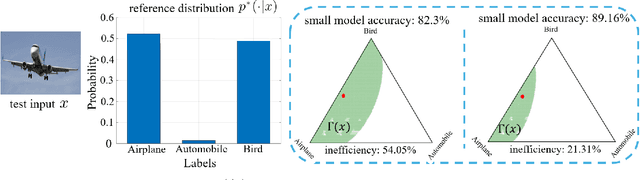
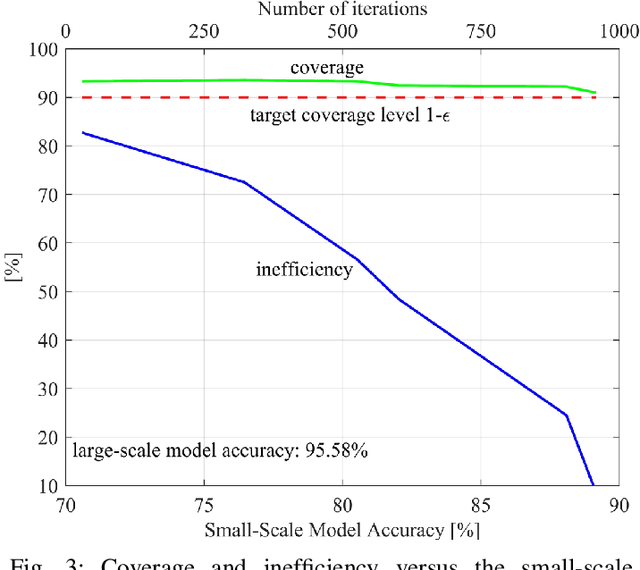
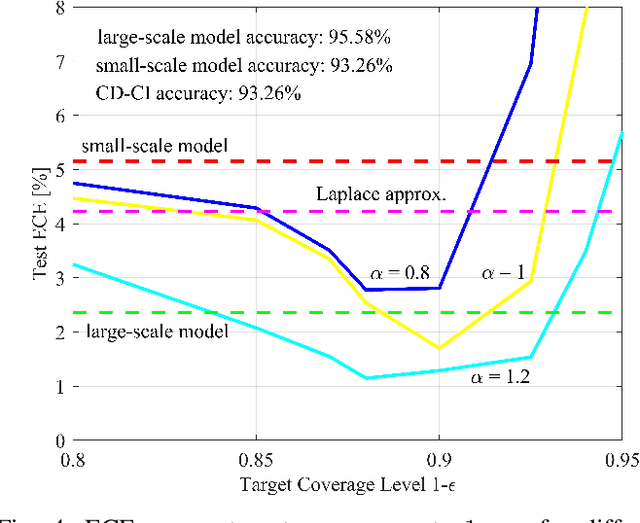
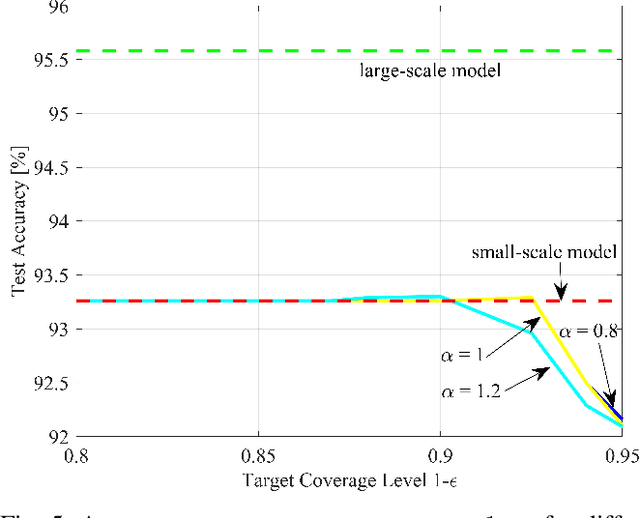
Deploying artificial intelligence (AI) models on edge devices involves a delicate balance between meeting stringent complexity constraints, such as limited memory and energy resources, and ensuring reliable performance in sensitive decision-making tasks. One way to enhance reliability is through uncertainty quantification via Bayesian inference. This approach, however, typically necessitates maintaining and running multiple models in an ensemble, which may exceed the computational limits of edge devices. This paper introduces a low-complexity methodology to address this challenge by distilling calibration information from a more complex model. In an offline phase, predictive probabilities generated by a high-complexity cloud-based model are leveraged to determine a threshold based on the typical divergence between the cloud and edge models. At run time, this threshold is used to construct credal sets -- ranges of predictive probabilities that are guaranteed, with a user-selected confidence level, to include the predictions of the cloud model. The credal sets are obtained through thresholding of a divergence measure in the simplex of predictive probabilities. Experiments on visual and language tasks demonstrate that the proposed approach, termed Conformalized Distillation for Credal Inference (CD-CI), significantly improves calibration performance compared to low-complexity Bayesian methods, such as Laplace approximation, making it a practical and efficient solution for edge AI deployments.

Verifiably Robust Conformal Prediction

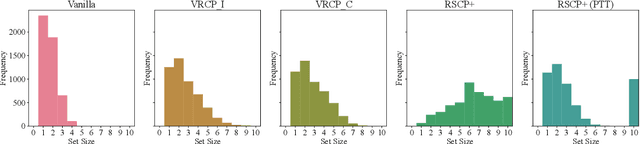
Conformal Prediction (CP) is a popular uncertainty quantification method that provides distribution-free, statistically valid prediction sets, assuming that training and test data are exchangeable. In such a case, CP's prediction sets are guaranteed to cover the (unknown) true test output with a user-specified probability. Nevertheless, this guarantee is violated when the data is subjected to adversarial attacks, which often result in a significant loss of coverage. Recently, several approaches have been put forward to recover CP guarantees in this setting. These approaches leverage variations of randomised smoothing to produce conservative sets which account for the effect of the adversarial perturbations. They are, however, limited in that they only support $\ell^2$-bounded perturbations and classification tasks. This paper introduces \emph{VRCP (Verifiably Robust Conformal Prediction)}, a new framework that leverages recent neural network verification methods to recover coverage guarantees under adversarial attacks. Our VRCP method is the first to support perturbations bounded by arbitrary norms including $\ell^1$, $\ell^2$, and $\ell^\infty$, as well as regression tasks. We evaluate and compare our approach on image classification tasks (CIFAR10, CIFAR100, and TinyImageNet) and regression tasks for deep reinforcement learning environments. In every case, VRCP achieves above nominal coverage and yields significantly more efficient and informative prediction regions than the SotA.

Conformal Off-Policy Prediction for Multi-Agent Systems

Off-Policy Prediction (OPP), i.e., predicting the outcomes of a target policy using only data collected under a nominal (behavioural) policy, is a paramount problem in data-driven analysis of safety-critical systems where the deployment of a new policy may be unsafe. To achieve dependable off-policy predictions, recent work on Conformal Off-Policy Prediction (COPP) leverage the conformal prediction framework to derive prediction regions with probabilistic guarantees under the target process. Existing COPP methods can account for the distribution shifts induced by policy switching, but are limited to single-agent systems and scalar outcomes (e.g., rewards). In this work, we introduce MA-COPP, the first conformal prediction method to solve OPP problems involving multi-agent systems, deriving joint prediction regions for all agents' trajectories when one or more "ego" agents change their policies. Unlike the single-agent scenario, this setting introduces higher complexity as the distribution shifts affect predictions for all agents, not just the ego agents, and the prediction task involves full multi-dimensional trajectories, not just reward values. A key contribution of MA-COPP is to avoid enumeration or exhaustive search of the output space of agent trajectories, which is instead required by existing COPP methods to construct the prediction region. We achieve this by showing that an over-approximation of the true JPR can be constructed, without enumeration, from the maximum density ratio of the JPR trajectories. We evaluate the effectiveness of MA-COPP in multi-agent systems from the PettingZoo library and the F1TENTH autonomous racing environment, achieving nominal coverage in higher dimensions and various shift settings.

Counterfactual Influence in Markov Decision Processes

Our work addresses a fundamental problem in the context of counterfactual inference for Markov Decision Processes (MDPs). Given an MDP path $\tau$, this kind of inference allows us to derive counterfactual paths $\tau'$ describing what-if versions of $\tau$ obtained under different action sequences than those observed in $\tau$. However, as the counterfactual states and actions deviate from the observed ones over time, the observation $\tau$ may no longer influence the counterfactual world, meaning that the analysis is no longer tailored to the individual observation, resulting in interventional outcomes rather than counterfactual ones. Even though this issue specifically affects the popular Gumbel-max structural causal model used for MDP counterfactuals, it has remained overlooked until now. In this work, we introduce a formal characterisation of influence based on comparing counterfactual and interventional distributions. We devise an algorithm to construct counterfactual models that automatically satisfy influence constraints. Leveraging such models, we derive counterfactual policies that are not just optimal for a given reward structure but also remain tailored to the observed path. Even though there is an unavoidable trade-off between policy optimality and strength of influence constraints, our experiments demonstrate that it is possible to derive (near-)optimal policies while remaining under the influence of the observation.

Learning-Based Approaches to Predictive Monitoring with Conformal Statistical Guarantees

This tutorial focuses on efficient methods to predictive monitoring (PM), the problem of detecting at runtime future violations of a given requirement from the current state of a system. While performing model checking at runtime would offer a precise solution to the PM problem, it is generally computationally expensive. To address this scalability issue, several lightweight approaches based on machine learning have recently been proposed. These approaches work by learning an approximate yet efficient surrogate (deep learning) model of the expensive model checker. A key challenge remains to ensure reliable predictions, especially in safety-critical applications. We review our recent work on predictive monitoring, one of the first to propose learning-based approximations for CPS verification of temporal logic specifications and the first in this context to apply conformal prediction (CP) for rigorous uncertainty quantification. These CP-based uncertainty estimators offer statistical guarantees regarding the generalization error of the learning model, and they can be used to determine unreliable predictions that should be rejected. In this tutorial, we present a general and comprehensive framework summarizing our approach to the predictive monitoring of CPSs, examining in detail several variants determined by three main dimensions: system dynamics (deterministic, non-deterministic, stochastic), state observability, and semantics of requirements' satisfaction (Boolean or quantitative).

Probabilistic Reach-Avoid for Bayesian Neural Networks

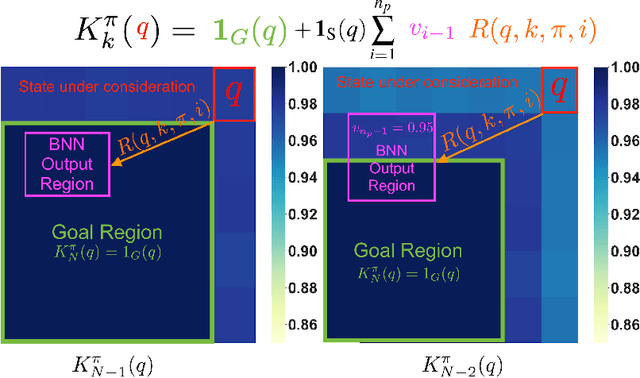
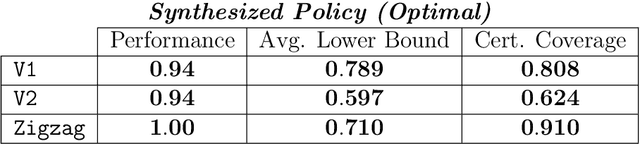
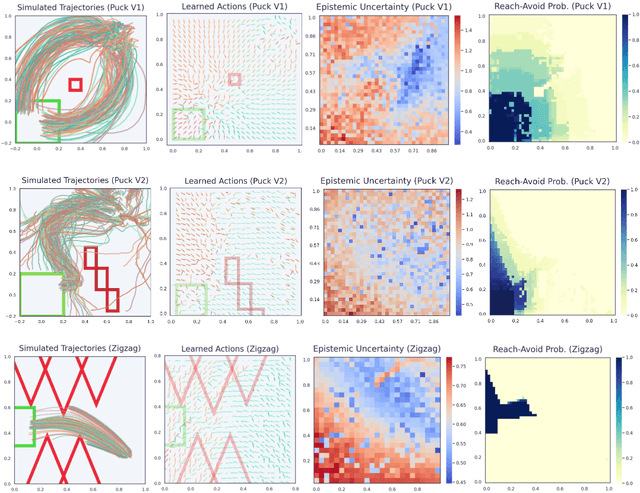
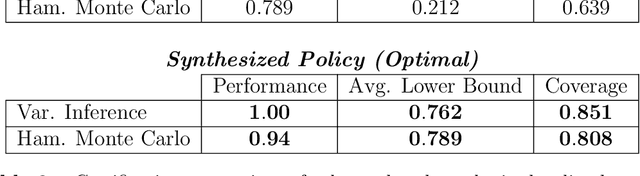
Model-based reinforcement learning seeks to simultaneously learn the dynamics of an unknown stochastic environment and synthesise an optimal policy for acting in it. Ensuring the safety and robustness of sequential decisions made through a policy in such an environment is a key challenge for policies intended for safety-critical scenarios. In this work, we investigate two complementary problems: first, computing reach-avoid probabilities for iterative predictions made with dynamical models, with dynamics described by Bayesian neural network (BNN); second, synthesising control policies that are optimal with respect to a given reach-avoid specification (reaching a "target" state, while avoiding a set of "unsafe" states) and a learned BNN model. Our solution leverages interval propagation and backward recursion techniques to compute lower bounds for the probability that a policy's sequence of actions leads to satisfying the reach-avoid specification. Such computed lower bounds provide safety certification for the given policy and BNN model. We then introduce control synthesis algorithms to derive policies maximizing said lower bounds on the safety probability. We demonstrate the effectiveness of our method on a series of control benchmarks characterized by learned BNN dynamics models. On our most challenging benchmark, compared to purely data-driven policies the optimal synthesis algorithm is able to provide more than a four-fold increase in the number of certifiable states and more than a three-fold increase in the average guaranteed reach-avoid probability.