Robust Counterfactual Inference in Markov Decision Processes
Paper and Code
Feb 19, 2025


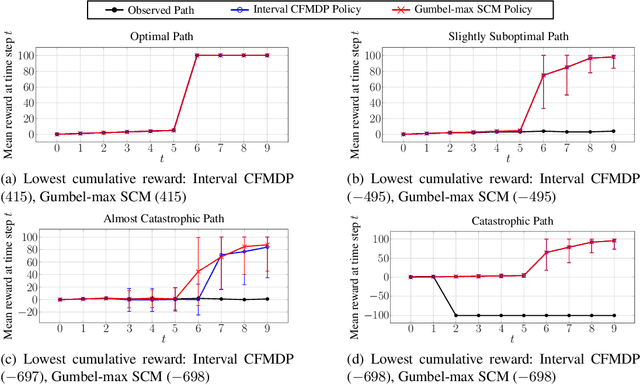
This paper addresses a key limitation in existing counterfactual inference methods for Markov Decision Processes (MDPs). Current approaches assume a specific causal model to make counterfactuals identifiable. However, there are usually many causal models that align with the observational and interventional distributions of an MDP, each yielding different counterfactual distributions, so fixing a particular causal model limits the validity (and usefulness) of counterfactual inference. We propose a novel non-parametric approach that computes tight bounds on counterfactual transition probabilities across all compatible causal models. Unlike previous methods that require solving prohibitively large optimisation problems (with variables that grow exponentially in the size of the MDP), our approach provides closed-form expressions for these bounds, making computation highly efficient and scalable for non-trivial MDPs. Once such an interval counterfactual MDP is constructed, our method identifies robust counterfactual policies that optimise the worst-case reward w.r.t. the uncertain interval MDP probabilities. We evaluate our method on various case studies, demonstrating improved robustness over existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge