Conformal Off-Policy Prediction for Multi-Agent Systems

Off-Policy Prediction (OPP), i.e., predicting the outcomes of a target policy using only data collected under a nominal (behavioural) policy, is a paramount problem in data-driven analysis of safety-critical systems where the deployment of a new policy may be unsafe. To achieve dependable off-policy predictions, recent work on Conformal Off-Policy Prediction (COPP) leverage the conformal prediction framework to derive prediction regions with probabilistic guarantees under the target process. Existing COPP methods can account for the distribution shifts induced by policy switching, but are limited to single-agent systems and scalar outcomes (e.g., rewards). In this work, we introduce MA-COPP, the first conformal prediction method to solve OPP problems involving multi-agent systems, deriving joint prediction regions for all agents' trajectories when one or more "ego" agents change their policies. Unlike the single-agent scenario, this setting introduces higher complexity as the distribution shifts affect predictions for all agents, not just the ego agents, and the prediction task involves full multi-dimensional trajectories, not just reward values. A key contribution of MA-COPP is to avoid enumeration or exhaustive search of the output space of agent trajectories, which is instead required by existing COPP methods to construct the prediction region. We achieve this by showing that an over-approximation of the true JPR can be constructed, without enumeration, from the maximum density ratio of the JPR trajectories. We evaluate the effectiveness of MA-COPP in multi-agent systems from the PettingZoo library and the F1TENTH autonomous racing environment, achieving nominal coverage in higher dimensions and various shift settings.

Counterfactual Influence in Markov Decision Processes

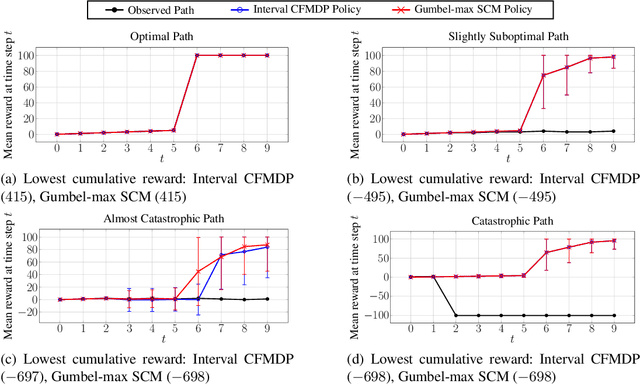
Our work addresses a fundamental problem in the context of counterfactual inference for Markov Decision Processes (MDPs). Given an MDP path $\tau$, this kind of inference allows us to derive counterfactual paths $\tau'$ describing what-if versions of $\tau$ obtained under different action sequences than those observed in $\tau$. However, as the counterfactual states and actions deviate from the observed ones over time, the observation $\tau$ may no longer influence the counterfactual world, meaning that the analysis is no longer tailored to the individual observation, resulting in interventional outcomes rather than counterfactual ones. Even though this issue specifically affects the popular Gumbel-max structural causal model used for MDP counterfactuals, it has remained overlooked until now. In this work, we introduce a formal characterisation of influence based on comparing counterfactual and interventional distributions. We devise an algorithm to construct counterfactual models that automatically satisfy influence constraints. Leveraging such models, we derive counterfactual policies that are not just optimal for a given reward structure but also remain tailored to the observed path. Even though there is an unavoidable trade-off between policy optimality and strength of influence constraints, our experiments demonstrate that it is possible to derive (near-)optimal policies while remaining under the influence of the observation.

Assume-Guarantee Reinforcement Learning

We present a modular approach to \emph{reinforcement learning} (RL) in environments consisting of simpler components evolving in parallel. A monolithic view of such modular environments may be prohibitively large to learn, or may require unrealizable communication between the components in the form of a centralized controller. Our proposed approach is based on the assume-guarantee paradigm where the optimal control for the individual components is synthesized in isolation by making \emph{assumptions} about the behaviors of neighboring components, and providing \emph{guarantees} about their own behavior. We express these \emph{assume-guarantee contracts} as regular languages and provide automatic translations to scalar rewards to be used in RL. By combining local probabilities of satisfaction for each component, we provide a lower bound on the probability of satisfaction of the complete system. By solving a Markov game for each component, RL can produce a controller for each component that maximizes this lower bound. The controller utilizes the information it receives through communication, observations, and any knowledge of a coarse model of other agents. We experimentally demonstrate the efficiency of the proposed approach on a variety of case studies.

Towards Causal Temporal Reasoning for Markov Decision Processes

We introduce a new probabilistic temporal logic for the verification of Markov Decision Processes (MDP). Our logic is the first to include operators for causal reasoning, allowing us to express interventional and counterfactual queries. Given a path formula $\phi$, an interventional property is concerned with the satisfaction probability of $\phi$ if we apply a particular change $I$ to the MDP (e.g., switching to a different policy); a counterfactual allows us to compute, given an observed MDP path $\tau$, what the outcome of $\phi$ would have been had we applied $I$ in the past. For its ability to reason about different configurations of the MDP, our approach represents a departure from existing probabilistic temporal logics that can only reason about a fixed system configuration. From a syntactic viewpoint, we introduce a generalized counterfactual operator that subsumes both interventional and counterfactual probabilities as well as the traditional probabilistic operator found in e.g., PCTL. From a semantics viewpoint, our logic is interpreted over a structural causal model (SCM) translation of the MDP, which gives us a representation amenable to counterfactual reasoning. We provide a proof-of-concept evaluation of our logic on a reach-avoid task in a grid-world model.

Formal Policy Synthesis for Continuous-Space Systems via Reinforcement Learning

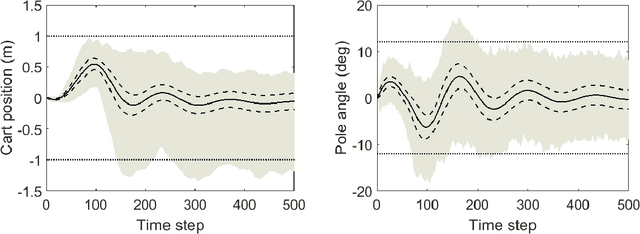
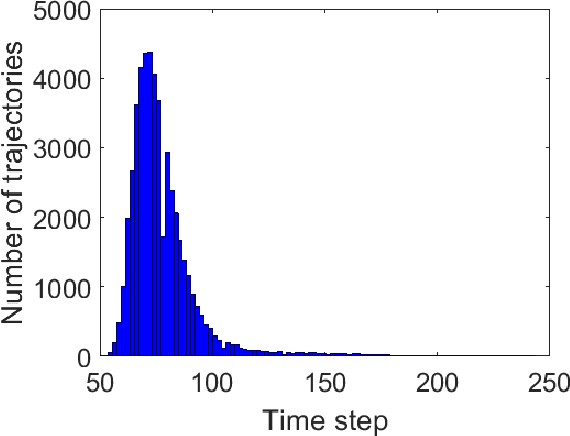
This paper studies data-driven techniques for satisfying temporal properties on unknown stochastic processes that have continuous spaces. We show how reinforcement learning (RL) can be applied for computing sub-optimal policies that are finite-memory and deterministic. We address properties expressed in linear temporal logic (LTL) and use their automaton representation to give a path-dependent reward function maximised via the RL algorithm. We develop theoretical foundations characterising the convergence of the learned policy to the optimal policy in the continuous space. To improve the performance of the learning on the constructed sparse reward function, we propose a sequential learning procedure based on a sequence of labelling functions obtained from the positive normal form of the LTL specification. We use this procedure to guide the RL algorithm towards the optimal policy. We show that our approach can give guaranteed lower bounds for the optimal satisfaction probability. The approach is demonstrated on a 4-dim cart-pole system and 6-dim boat driving problem.