Formal Policy Synthesis for Continuous-Space Systems via Reinforcement Learning

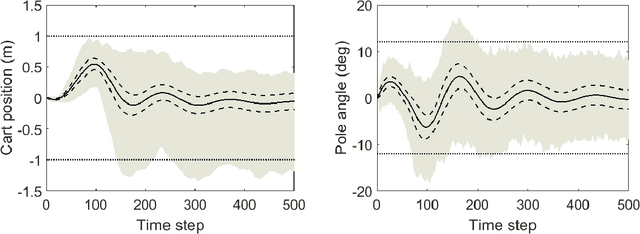
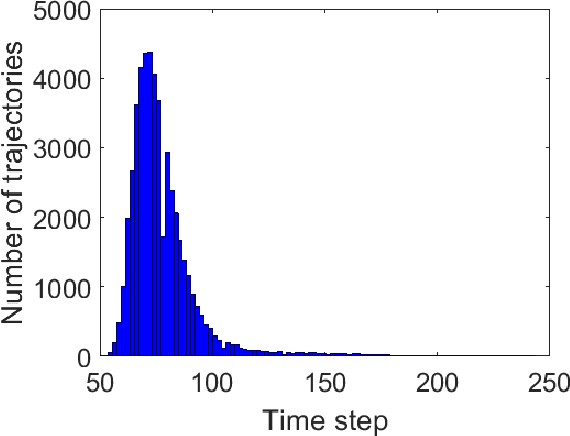
This paper studies data-driven techniques for satisfying temporal properties on unknown stochastic processes that have continuous spaces. We show how reinforcement learning (RL) can be applied for computing sub-optimal policies that are finite-memory and deterministic. We address properties expressed in linear temporal logic (LTL) and use their automaton representation to give a path-dependent reward function maximised via the RL algorithm. We develop theoretical foundations characterising the convergence of the learned policy to the optimal policy in the continuous space. To improve the performance of the learning on the constructed sparse reward function, we propose a sequential learning procedure based on a sequence of labelling functions obtained from the positive normal form of the LTL specification. We use this procedure to guide the RL algorithm towards the optimal policy. We show that our approach can give guaranteed lower bounds for the optimal satisfaction probability. The approach is demonstrated on a 4-dim cart-pole system and 6-dim boat driving problem.