Kernel-Based Learning of Safety Barriers

The rapid integration of AI algorithms in safety-critical applications such as autonomous driving and healthcare is raising significant concerns about the ability to meet stringent safety standards. Traditional tools for formal safety verification struggle with the black-box nature of AI-driven systems and lack the flexibility needed to scale to the complexity of real-world applications. In this paper, we present a data-driven approach for safety verification and synthesis of black-box systems with discrete-time stochastic dynamics. We employ the concept of control barrier certificates, which can guarantee safety of the system, and learn the certificate directly from a set of system trajectories. We use conditional mean embeddings to embed data from the system into a reproducing kernel Hilbert space (RKHS) and construct an RKHS ambiguity set that can be inflated to robustify the result to out-of-distribution behavior. We provide the theoretical results on how to apply the approach to general classes of temporal logic specifications beyond safety. For the data-driven computation of safety barriers, we leverage a finite Fourier expansion to cast a typically intractable semi-infinite optimization problem as a linear program. The resulting spectral barrier allows us to leverage the fast Fourier transform to generate the relaxed problem efficiently, offering a scalable yet distributionally robust framework for verifying safety. Our work moves beyond restrictive assumptions on system dynamics and uncertainty, as demonstrated on two case studies including a black-box system with a neural network controller.

LUCID: Learning-Enabled Uncertainty-Aware Certification of Stochastic Dynamical Systems

Ensuring the safety of AI-enabled systems, particularly in high-stakes domains such as autonomous driving and healthcare, has become increasingly critical. Traditional formal verification tools fall short when faced with systems that embed both opaque, black-box AI components and complex stochastic dynamics. To address these challenges, we introduce LUCID (Learning-enabled Uncertainty-aware Certification of stochastIc Dynamical systems), a verification engine for certifying safety of black-box stochastic dynamical systems from a finite dataset of random state transitions. As such, LUCID is the first known tool capable of establishing quantified safety guarantees for such systems. Thanks to its modular architecture and extensive documentation, LUCID is designed for easy extensibility. LUCID employs a data-driven methodology rooted in control barrier certificates, which are learned directly from system transition data, to ensure formal safety guarantees. We use conditional mean embeddings to embed data into a reproducing kernel Hilbert space (RKHS), where an RKHS ambiguity set is constructed that can be inflated to robustify the result to out-of-distribution behavior. A key innovation within LUCID is its use of a finite Fourier kernel expansion to reformulate a semi-infinite non-convex optimization problem into a tractable linear program. The resulting spectral barrier allows us to leverage the fast Fourier transform to generate the relaxed problem efficiently, offering a scalable yet distributionally robust framework for verifying safety. LUCID thus offers a robust and efficient verification framework, able to handle the complexities of modern black-box systems while providing formal guarantees of safety. These unique capabilities are demonstrated on challenging benchmarks.

Quasi-Newton Compatible Actor-Critic for Deterministic Policies

In this paper, we propose a second-order deterministic actor-critic framework in reinforcement learning that extends the classical deterministic policy gradient method to exploit curvature information of the performance function. Building on the concept of compatible function approximation for the critic, we introduce a quadratic critic that simultaneously preserves the true policy gradient and an approximation of the performance Hessian. A least-squares temporal difference learning scheme is then developed to estimate the quadratic critic parameters efficiently. This construction enables a quasi-Newton actor update using information learned by the critic, yielding faster convergence compared to first-order methods. The proposed approach is general and applicable to any differentiable policy class. Numerical examples demonstrate that the method achieves improved convergence and performance over standard deterministic actor-critic baselines.

BarrierBench : Evaluating Large Language Models for Safety Verification in Dynamical Systems

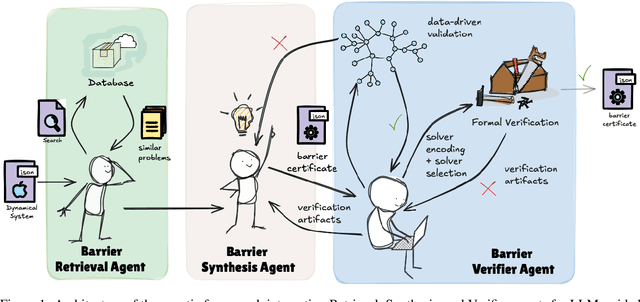
Safety verification of dynamical systems via barrier certificates is essential for ensuring correctness in autonomous applications. Synthesizing these certificates involves discovering mathematical functions with current methods suffering from poor scalability, dependence on carefully designed templates, and exhaustive or incremental function-space searches. They also demand substantial manual expertise--selecting templates, solvers, and hyperparameters, and designing sampling strategies--requiring both theoretical and practical knowledge traditionally shared through linguistic reasoning rather than formalized methods. This motivates a key question: can such expert reasoning be captured and operationalized by language models? We address this by introducing an LLM-based agentic framework for barrier certificate synthesis. The framework uses natural language reasoning to propose, refine, and validate candidate certificates, integrating LLM-driven template discovery with SMT-based verification, and supporting barrier-controller co-synthesis to ensure consistency between safety certificates and controllers. To evaluate this capability, we introduce BarrierBench, a benchmark of 100 dynamical systems spanning linear, nonlinear, discrete-time, and continuous-time settings. Our experiments assess not only the effectiveness of LLM-guided barrier synthesis but also the utility of retrieval-augmented generation and agentic coordination strategies in improving its reliability and performance. Across these tasks, the framework achieves more than 90% success in generating valid certificates. By releasing BarrierBench and the accompanying toolchain, we aim to establish a community testbed for advancing the integration of language-based reasoning with formal verification in dynamical systems. The benchmark is publicly available at https://hycodev.com/dataset/barrierbench

Blending Participatory Design and Artificial Awareness for Trustworthy Autonomous Vehicles

Current robotic agents, such as autonomous vehicles (AVs) and drones, need to deal with uncertain real-world environments with appropriate situational awareness (SA), risk awareness, coordination, and decision-making. The SymAware project strives to address this issue by designing an architecture for artificial awareness in multi-agent systems, enabling safe collaboration of autonomous vehicles and drones. However, these agents will also need to interact with human users (drivers, pedestrians, drone operators), which in turn requires an understanding of how to model the human in the interaction scenario, and how to foster trust and transparency between the agent and the human. In this work, we aim to create a data-driven model of a human driver to be integrated into our SA architecture, grounding our research in the principles of trustworthy human-agent interaction. To collect the data necessary for creating the model, we conducted a large-scale user-centered study on human-AV interaction, in which we investigate the interaction between the AV's transparency and the users' behavior. The contributions of this paper are twofold: First, we illustrate in detail our human-AV study and its findings, and second we present the resulting Markov chain models of the human driver computed from the study's data. Our results show that depending on the AV's transparency, the scenario's environment, and the users' demographics, we can obtain significant differences in the model's transitions.

Regret-Free Reinforcement Learning for LTL Specifications

Reinforcement learning (RL) is a promising method to learn optimal control policies for systems with unknown dynamics. In particular, synthesizing controllers for safety-critical systems based on high-level specifications, such as those expressed in temporal languages like linear temporal logic (LTL), presents a significant challenge in control systems research. Current RL-based methods designed for LTL tasks typically offer only asymptotic guarantees, which provide no insight into the transient performance during the learning phase. While running an RL algorithm, it is crucial to assess how close we are to achieving optimal behavior if we stop learning. In this paper, we present the first regret-free online algorithm for learning a controller that addresses the general class of LTL specifications over Markov decision processes (MDPs) with a finite set of states and actions. We begin by proposing a regret-free learning algorithm to solve infinite-horizon reach-avoid problems. For general LTL specifications, we show that the synthesis problem can be reduced to a reach-avoid problem when the graph structure is known. Additionally, we provide an algorithm for learning the graph structure, assuming knowledge of a minimum transition probability, which operates independently of the main regret-free algorithm.

T-Count Optimizing Genetic Algorithm for Quantum State Preparation

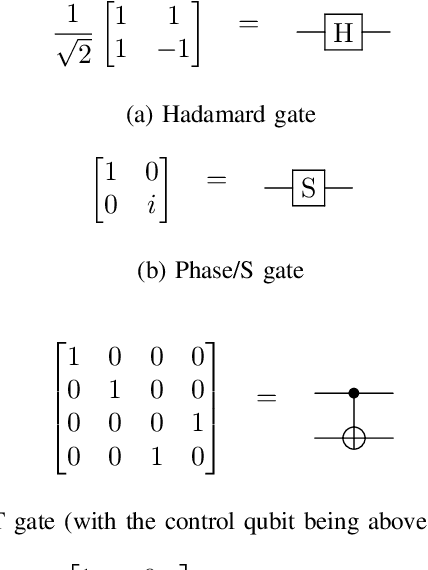
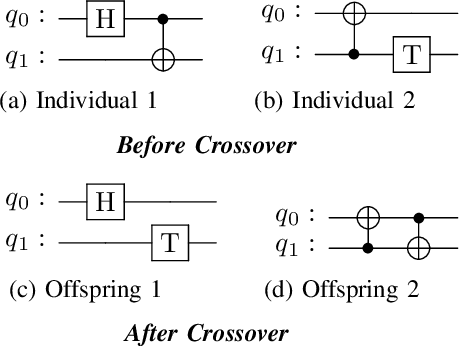
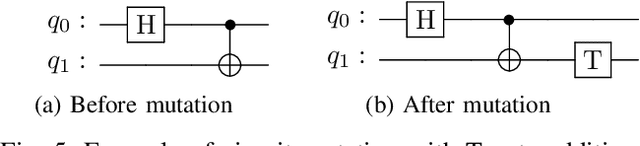
Quantum state preparation is a crucial process within numerous quantum algorithms, and the need for efficient initialization of quantum registers is ever increasing as demand for useful quantum computing grows. The problem arises as the number of qubits to be initialized grows, the circuits required to implement the desired state also exponentially increase in size leading to loss of fidelity to noise. This is mainly due to the susceptibility to environmental effects of the non-Clifford T gate, whose use should thus be reduced as much as possible. In this paper, we present and utilize a genetic algorithm for state preparation circuits consisting of gates from the Clifford + T gate set and optimize them in T-Count as to reduce the impact of noise. Whilst the method presented here does not always produce the most accurate circuits in terms of fidelity, it can generate high-fidelity, non-trivial quantum states such as quantum Fourier transform states. In addition, our algorithm does automatically generate fault tolerantly implementable solutions where the number of the most error prone components is reduced. We present an evaluation of the algorithm when trialed against preparing random, Poisson probability distribution, W, GHZ, and quantum Fourier transform states. We also experimentally demonstrate the scalability issues as qubit count increases, which highlights the need for further optimization of the search process.

Safe Reach Set Computation via Neural Barrier Certificates

We present a novel technique for online safety verification of autonomous systems, which performs reachability analysis efficiently for both bounded and unbounded horizons by employing neural barrier certificates. Our approach uses barrier certificates given by parameterized neural networks that depend on a given initial set, unsafe sets, and time horizon. Such networks are trained efficiently offline using system simulations sampled from regions of the state space. We then employ a meta-neural network to generalize the barrier certificates to state space regions that are outside the training set. These certificates are generated and validated online as sound over-approximations of the reachable states, thus either ensuring system safety or activating appropriate alternative actions in unsafe scenarios. We demonstrate our technique on case studies from linear models to nonlinear control-dependent models for online autonomous driving scenarios.

Data-Driven Distributionally Robust Safety Verification Using Barrier Certificates and Conditional Mean Embeddings

Algorithmic verification of realistic systems to satisfy safety and other temporal requirements has suffered from poor scalability of the employed formal approaches. To design systems with rigorous guarantees, many approaches still rely on exact models of the underlying systems. Since this assumption can rarely be met in practice, models have to be inferred from measurement data or are bypassed completely. Whilst former usually requires the model structure to be known a-priori and immense amounts of data to be available, latter gives rise to a plethora of restrictive mathematical assumptions about the unknown dynamics. In a pursuit of developing scalable formal verification algorithms without shifting the problem to unrealistic assumptions, we employ the concept of barrier certificates, which can guarantee safety of the system, and learn the certificate directly from a compact set of system trajectories. We use conditional mean embeddings to embed data from the system into a reproducing kernel Hilbert space (RKHS) and construct an RKHS ambiguity set that can be inflated to robustify the result w.r.t. a set of plausible transition kernels. We show how to solve the resulting program efficiently using sum-of-squares optimization and a Gaussian process envelope. Our approach lifts the need for restrictive assumptions on the system dynamics and uncertainty, and suggests an improvement in the sample complexity of verifying the safety of a system on a tested case study compared to a state-of-the-art approach.

Awareness in robotics: An early perspective from the viewpoint of the EIC Pathfinder Challenge "Awareness Inside''

Consciousness has been historically a heavily debated topic in engineering, science, and philosophy. On the contrary, awareness had less success in raising the interest of scholars in the past. However, things are changing as more and more researchers are getting interested in answering questions concerning what awareness is and how it can be artificially generated. The landscape is rapidly evolving, with multiple voices and interpretations of the concept being conceived and techniques being developed. The goal of this paper is to summarize and discuss the ones among these voices connected with projects funded by the EIC Pathfinder Challenge called ``Awareness Inside'', a nonrecurring call for proposals within Horizon Europe designed specifically for fostering research on natural and synthetic awareness. In this perspective, we dedicate special attention to challenges and promises of applying synthetic awareness in robotics, as the development of mature techniques in this new field is expected to have a special impact on generating more capable and trustworthy embodied systems.