Data-Driven Verification under Signal Temporal Logic Constraints
Paper and Code
May 08, 2020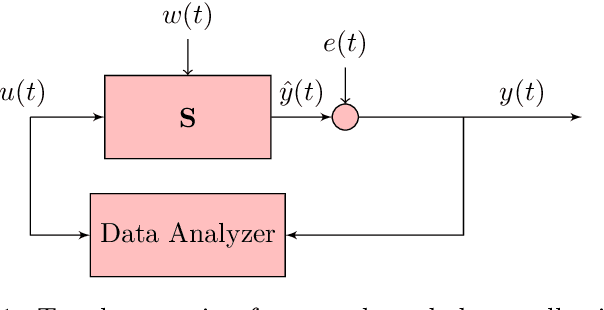
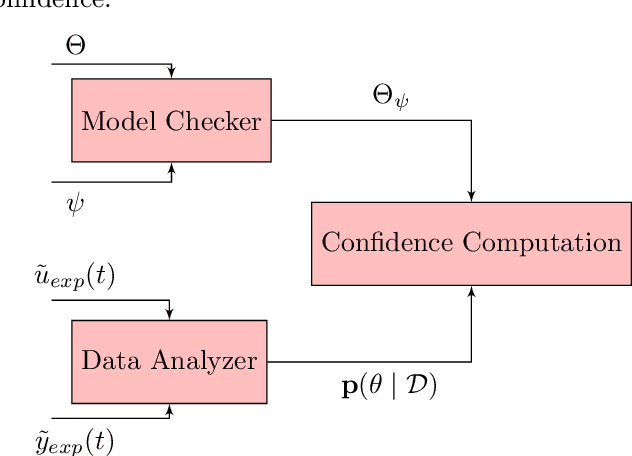
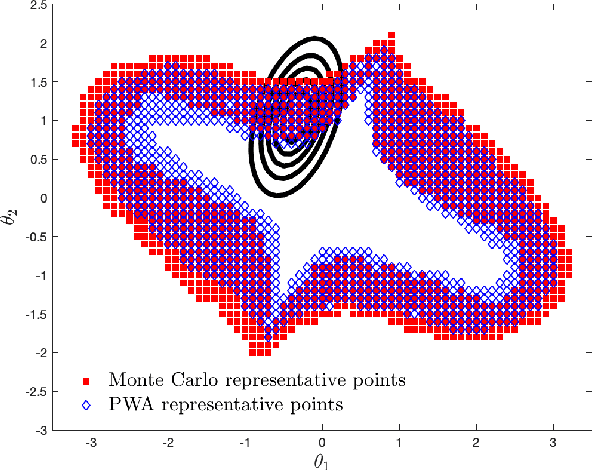
We consider systems under uncertainty whose dynamics are partially unknown. Our aim is to study satisfaction of temporal logic properties by trajectories of such systems. We express these properties as signal temporal logic formulas and check if the probability of satisfying the property is at least a given threshold. Since the dynamics are parameterized and partially unknown, we collect data from the system and employ Bayesian inference techniques to associate a confidence value to the satisfaction of the property. The main novelty of our approach is to combine both data-driven and model-based techniques in order to have a two-layer probabilistic reasoning over the behavior of the system: one layer is related to the stochastic noise inside the system and the next layer is related to the noisy data collected from the system. We provide approximate algorithms for computing the confidence for linear dynamical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge