Assume-Guarantee Reinforcement Learning

We present a modular approach to \emph{reinforcement learning} (RL) in environments consisting of simpler components evolving in parallel. A monolithic view of such modular environments may be prohibitively large to learn, or may require unrealizable communication between the components in the form of a centralized controller. Our proposed approach is based on the assume-guarantee paradigm where the optimal control for the individual components is synthesized in isolation by making \emph{assumptions} about the behaviors of neighboring components, and providing \emph{guarantees} about their own behavior. We express these \emph{assume-guarantee contracts} as regular languages and provide automatic translations to scalar rewards to be used in RL. By combining local probabilities of satisfaction for each component, we provide a lower bound on the probability of satisfaction of the complete system. By solving a Markov game for each component, RL can produce a controller for each component that maximizes this lower bound. The controller utilizes the information it receives through communication, observations, and any knowledge of a coarse model of other agents. We experimentally demonstrate the efficiency of the proposed approach on a variety of case studies.

Omega-Regular Decision Processes

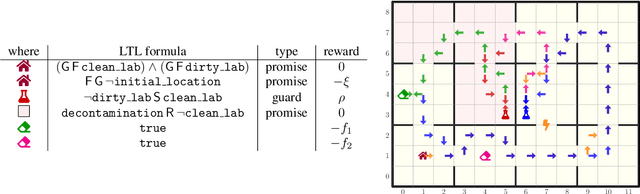
Regular decision processes (RDPs) are a subclass of non-Markovian decision processes where the transition and reward functions are guarded by some regular property of the past (a lookback). While RDPs enable intuitive and succinct representation of non-Markovian decision processes, their expressive power coincides with finite-state Markov decision processes (MDPs). We introduce omega-regular decision processes (ODPs) where the non-Markovian aspect of the transition and reward functions are extended to an omega-regular lookahead over the system evolution. Semantically, these lookaheads can be considered as promises made by the decision maker or the learning agent about her future behavior. In particular, we assume that, if the promised lookaheads are not met, then the payoff to the decision maker is $\bot$ (least desirable payoff), overriding any rewards collected by the decision maker. We enable optimization and learning for ODPs under the discounted-reward objective by reducing them to lexicographic optimization and learning over finite MDPs. We present experimental results demonstrating the effectiveness of the proposed reduction.

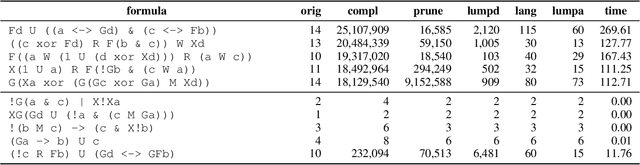
A PAC Learning Algorithm for LTL and Omega-regular Objectives in MDPs

Linear temporal logic (LTL) and omega-regular objectives -- a superset of LTL -- have seen recent use as a way to express non-Markovian objectives in reinforcement learning. We introduce a model-based probably approximately correct (PAC) learning algorithm for omega-regular objectives in Markov decision processes. Unlike prior approaches, our algorithm learns from sampled trajectories of the system and does not require prior knowledge of the system's topology.

Omega-Regular Reward Machines

Reinforcement learning (RL) is a powerful approach for training agents to perform tasks, but designing an appropriate reward mechanism is critical to its success. However, in many cases, the complexity of the learning objectives goes beyond the capabilities of the Markovian assumption, necessitating a more sophisticated reward mechanism. Reward machines and omega-regular languages are two formalisms used to express non-Markovian rewards for quantitative and qualitative objectives, respectively. This paper introduces omega-regular reward machines, which integrate reward machines with omega-regular languages to enable an expressive and effective reward mechanism for RL. We present a model-free RL algorithm to compute epsilon-optimal strategies against omega-egular reward machines and evaluate the effectiveness of the proposed algorithm through experiments.

Policy Synthesis and Reinforcement Learning for Discounted LTL

The difficulty of manually specifying reward functions has led to an interest in using linear temporal logic (LTL) to express objectives for reinforcement learning (RL). However, LTL has the downside that it is sensitive to small perturbations in the transition probabilities, which prevents probably approximately correct (PAC) learning without additional assumptions. Time discounting provides a way of removing this sensitivity, while retaining the high expressivity of the logic. We study the use of discounted LTL for policy synthesis in Markov decision processes with unknown transition probabilities, and show how to reduce discounted LTL to discounted-sum reward via a reward machine when all discount factors are identical.

Recursive Reinforcement Learning

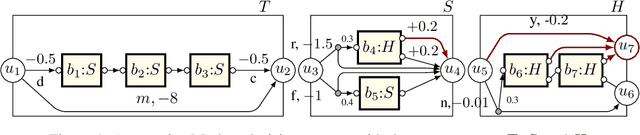
Recursion is the fundamental paradigm to finitely describe potentially infinite objects. As state-of-the-art reinforcement learning (RL) algorithms cannot directly reason about recursion, they must rely on the practitioner's ingenuity in designing a suitable "flat" representation of the environment. The resulting manual feature constructions and approximations are cumbersome and error-prone; their lack of transparency hampers scalability. To overcome these challenges, we develop RL algorithms capable of computing optimal policies in environments described as a collection of Markov decision processes (MDPs) that can recursively invoke one another. Each constituent MDP is characterized by several entry and exit points that correspond to input and output values of these invocations. These recursive MDPs (or RMDPs) are expressively equivalent to probabilistic pushdown systems (with call-stack playing the role of the pushdown stack), and can model probabilistic programs with recursive procedural calls. We introduce Recursive Q-learning -- a model-free RL algorithm for RMDPs -- and prove that it converges for finite, single-exit and deterministic multi-exit RMDPs under mild assumptions.

Alternating Good-for-MDP Automata

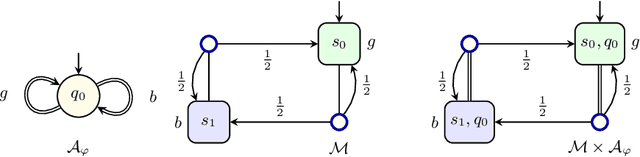
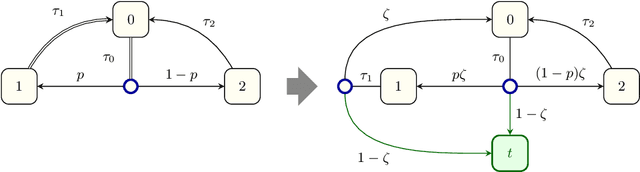
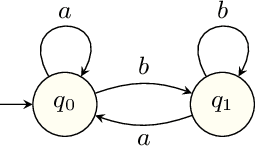
When omega-regular objectives were first proposed in model-free reinforcement learning (RL) for controlling MDPs, deterministic Rabin automata were used in an attempt to provide a direct translation from their transitions to scalar values. While these translations failed, it has turned out that it is possible to repair them by using good-for-MDPs (GFM) B\"uchi automata instead. These are nondeterministic B\"uchi automata with a restricted type of nondeterminism, albeit not as restricted as in good-for-games automata. Indeed, deterministic Rabin automata have a pretty straightforward translation to such GFM automata, which is bi-linear in the number of states and pairs. Interestingly, the same cannot be said for deterministic Streett automata: a translation to nondeterministic Rabin or B\"uchi automata comes at an exponential cost, even without requiring the target automaton to be good-for-MDPs. Do we have to pay more than that to obtain a good-for-MDP automaton? The surprising answer is that we have to pay significantly less when we instead expand the good-for-MDP property to alternating automata: like the nondeterministic GFM automata obtained from deterministic Rabin automata, the alternating good-for-MDP automata we produce from deterministic Streett automata are bi-linear in the the size of the deterministic automaton and its index, and can therefore be exponentially more succinct than minimal nondeterministic B\"uchi automata.

Mungojerrie: Reinforcement Learning of Linear-Time Objectives

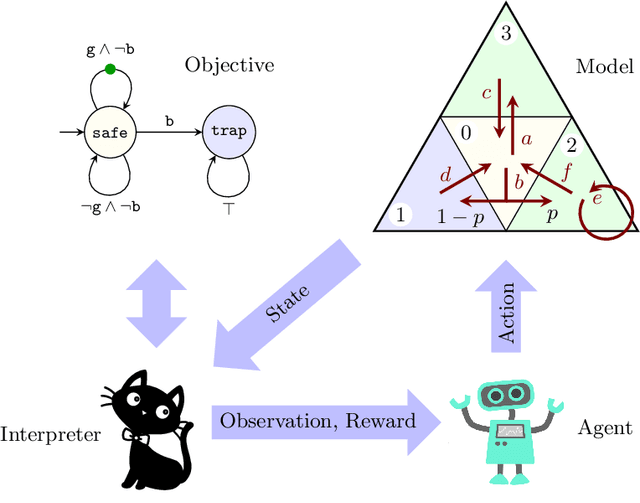
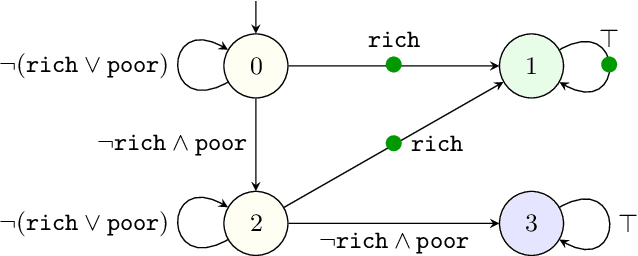
Reinforcement learning synthesizes controllers without prior knowledge of the system. At each timestep, a reward is given. The controllers optimize the discounted sum of these rewards. Applying this class of algorithms requires designing a reward scheme, which is typically done manually. The designer must ensure that their intent is accurately captured. This may not be trivial, and is prone to error. An alternative to this manual programming, akin to programming directly in assembly, is to specify the objective in a formal language and have it "compiled" to a reward scheme. Mungojerrie (https://plv.colorado.edu/mungojerrie/) is a tool for testing reward schemes for $\omega$-regular objectives on finite models. The tool contains reinforcement learning algorithms and a probabilistic model checker. Mungojerrie supports models specified in PRISM and $\omega$-automata specified in HOA.

Model-free Reinforcement Learning for Branching Markov Decision Processes

We study reinforcement learning for the optimal control of Branching Markov Decision Processes (BMDPs), a natural extension of (multitype) Branching Markov Chains (BMCs). The state of a (discrete-time) BMCs is a collection of entities of various types that, while spawning other entities, generate a payoff. In comparison with BMCs, where the evolution of a each entity of the same type follows the same probabilistic pattern, BMDPs allow an external controller to pick from a range of options. This permits us to study the best/worst behaviour of the system. We generalise model-free reinforcement learning techniques to compute an optimal control strategy of an unknown BMDP in the limit. We present results of an implementation that demonstrate the practicality of the approach.