Autonomous Vehicles Path Planning under Temporal Logic Specifications

Path planning is an essential component of autonomous driving. A global planner is responsible for the high-level planning. It basically performs a shortest-path search on a known map, thereby defining waypoints used to control the local (low-level) planner. Local planning is a runtime verification method which is repeatedly run on the vehicle itself in real-time, so as to find the optimal short-horizon path which leads to the desired waypoint in a way which is both efficient and safe. The challenge is that the local planner has to take into account repeatedly incoming updates about the information available of the environment. In addition, it performs a complex task, as it has to take into account a large variety of requirements, originating from the necessity of collision avoidance with obstacles, respecting traffic rules, sticking to regulatory requirements, and lastly to reach the next waypoint efficiently. In this paper, we describe a logic-based specification mechanism which fulfills all these requirements.

Omega-Regular Decision Processes

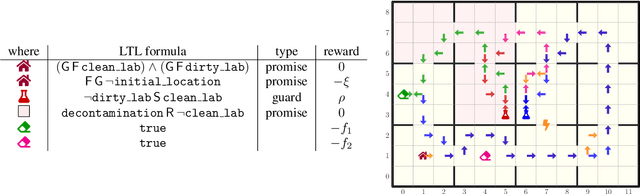
Regular decision processes (RDPs) are a subclass of non-Markovian decision processes where the transition and reward functions are guarded by some regular property of the past (a lookback). While RDPs enable intuitive and succinct representation of non-Markovian decision processes, their expressive power coincides with finite-state Markov decision processes (MDPs). We introduce omega-regular decision processes (ODPs) where the non-Markovian aspect of the transition and reward functions are extended to an omega-regular lookahead over the system evolution. Semantically, these lookaheads can be considered as promises made by the decision maker or the learning agent about her future behavior. In particular, we assume that, if the promised lookaheads are not met, then the payoff to the decision maker is $\bot$ (least desirable payoff), overriding any rewards collected by the decision maker. We enable optimization and learning for ODPs under the discounted-reward objective by reducing them to lexicographic optimization and learning over finite MDPs. We present experimental results demonstrating the effectiveness of the proposed reduction.

AGNES: Abstraction-guided Framework for Deep Neural Networks Security

Deep Neural Networks (DNNs) are becoming widespread, particularly in safety-critical areas. One prominent application is image recognition in autonomous driving, where the correct classification of objects, such as traffic signs, is essential for safe driving. Unfortunately, DNNs are prone to backdoors, meaning that they concentrate on attributes of the image that should be irrelevant for their correct classification. Backdoors are integrated into a DNN during training, either with malicious intent (such as a manipulated training process, because of which a yellow sticker always leads to a traffic sign being recognised as a stop sign) or unintentional (such as a rural background leading to any traffic sign being recognised as animal crossing, because of biased training data). In this paper, we introduce AGNES, a tool to detect backdoors in DNNs for image recognition. We discuss the principle approach on which AGNES is based. Afterwards, we show that our tool performs better than many state-of-the-art methods for multiple relevant case studies.

Omega-Regular Reward Machines

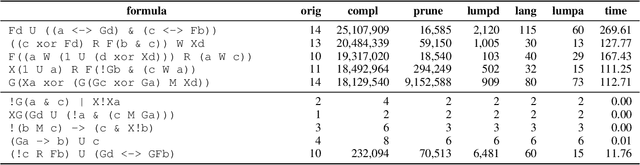
Reinforcement learning (RL) is a powerful approach for training agents to perform tasks, but designing an appropriate reward mechanism is critical to its success. However, in many cases, the complexity of the learning objectives goes beyond the capabilities of the Markovian assumption, necessitating a more sophisticated reward mechanism. Reward machines and omega-regular languages are two formalisms used to express non-Markovian rewards for quantitative and qualitative objectives, respectively. This paper introduces omega-regular reward machines, which integrate reward machines with omega-regular languages to enable an expressive and effective reward mechanism for RL. We present a model-free RL algorithm to compute epsilon-optimal strategies against omega-egular reward machines and evaluate the effectiveness of the proposed algorithm through experiments.

Backdoor Mitigation in Deep Neural Networks via Strategic Retraining

Deep Neural Networks (DNN) are becoming increasingly more important in assisted and automated driving. Using such entities which are obtained using machine learning is inevitable: tasks such as recognizing traffic signs cannot be developed reasonably using traditional software development methods. DNN however do have the problem that they are mostly black boxes and therefore hard to understand and debug. One particular problem is that they are prone to hidden backdoors. This means that the DNN misclassifies its input, because it considers properties that should not be decisive for the output. Backdoors may either be introduced by malicious attackers or by inappropriate training. In any case, detecting and removing them is important in the automotive area, as they might lead to safety violations with potentially severe consequences. In this paper, we introduce a novel method to remove backdoors. Our method works for both intentional as well as unintentional backdoors. We also do not require prior knowledge about the shape or distribution of backdoors. Experimental evidence shows that our method performs well on several medium-sized examples.

Recursive Reinforcement Learning

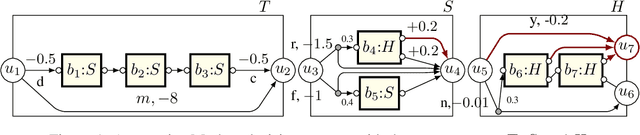
Recursion is the fundamental paradigm to finitely describe potentially infinite objects. As state-of-the-art reinforcement learning (RL) algorithms cannot directly reason about recursion, they must rely on the practitioner's ingenuity in designing a suitable "flat" representation of the environment. The resulting manual feature constructions and approximations are cumbersome and error-prone; their lack of transparency hampers scalability. To overcome these challenges, we develop RL algorithms capable of computing optimal policies in environments described as a collection of Markov decision processes (MDPs) that can recursively invoke one another. Each constituent MDP is characterized by several entry and exit points that correspond to input and output values of these invocations. These recursive MDPs (or RMDPs) are expressively equivalent to probabilistic pushdown systems (with call-stack playing the role of the pushdown stack), and can model probabilistic programs with recursive procedural calls. We introduce Recursive Q-learning -- a model-free RL algorithm for RMDPs -- and prove that it converges for finite, single-exit and deterministic multi-exit RMDPs under mild assumptions.

Alternating Good-for-MDP Automata

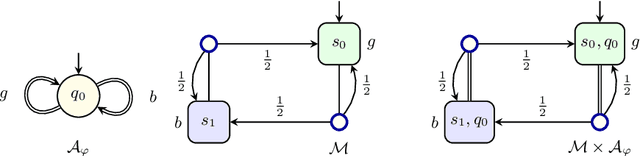
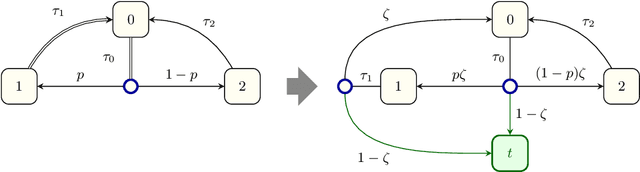
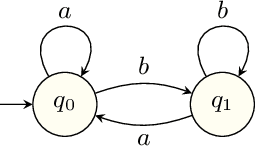
When omega-regular objectives were first proposed in model-free reinforcement learning (RL) for controlling MDPs, deterministic Rabin automata were used in an attempt to provide a direct translation from their transitions to scalar values. While these translations failed, it has turned out that it is possible to repair them by using good-for-MDPs (GFM) B\"uchi automata instead. These are nondeterministic B\"uchi automata with a restricted type of nondeterminism, albeit not as restricted as in good-for-games automata. Indeed, deterministic Rabin automata have a pretty straightforward translation to such GFM automata, which is bi-linear in the number of states and pairs. Interestingly, the same cannot be said for deterministic Streett automata: a translation to nondeterministic Rabin or B\"uchi automata comes at an exponential cost, even without requiring the target automaton to be good-for-MDPs. Do we have to pay more than that to obtain a good-for-MDP automaton? The surprising answer is that we have to pay significantly less when we instead expand the good-for-MDP property to alternating automata: like the nondeterministic GFM automata obtained from deterministic Rabin automata, the alternating good-for-MDP automata we produce from deterministic Streett automata are bi-linear in the the size of the deterministic automaton and its index, and can therefore be exponentially more succinct than minimal nondeterministic B\"uchi automata.

Mungojerrie: Reinforcement Learning of Linear-Time Objectives

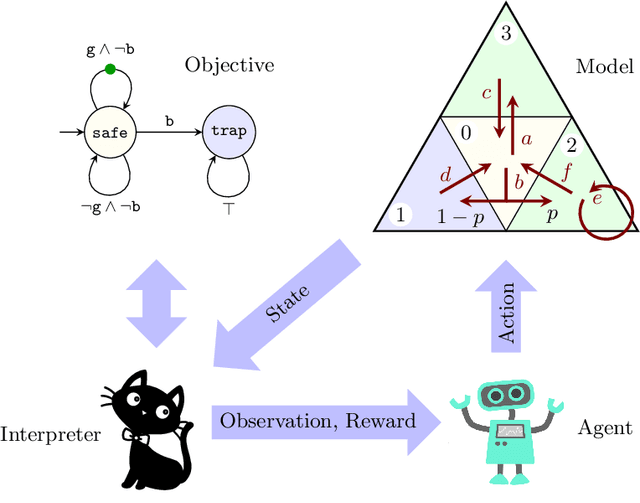
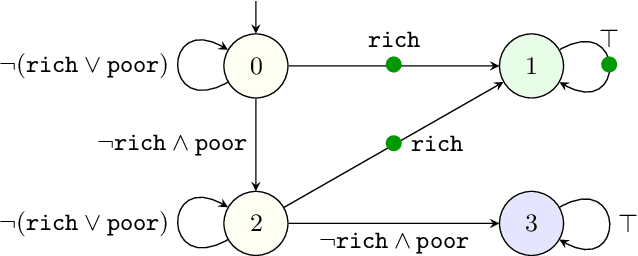
Reinforcement learning synthesizes controllers without prior knowledge of the system. At each timestep, a reward is given. The controllers optimize the discounted sum of these rewards. Applying this class of algorithms requires designing a reward scheme, which is typically done manually. The designer must ensure that their intent is accurately captured. This may not be trivial, and is prone to error. An alternative to this manual programming, akin to programming directly in assembly, is to specify the objective in a formal language and have it "compiled" to a reward scheme. Mungojerrie (https://plv.colorado.edu/mungojerrie/) is a tool for testing reward schemes for $\omega$-regular objectives on finite models. The tool contains reinforcement learning algorithms and a probabilistic model checker. Mungojerrie supports models specified in PRISM and $\omega$-automata specified in HOA.

Model-free Reinforcement Learning for Branching Markov Decision Processes

We study reinforcement learning for the optimal control of Branching Markov Decision Processes (BMDPs), a natural extension of (multitype) Branching Markov Chains (BMCs). The state of a (discrete-time) BMCs is a collection of entities of various types that, while spawning other entities, generate a payoff. In comparison with BMCs, where the evolution of a each entity of the same type follows the same probabilistic pattern, BMDPs allow an external controller to pick from a range of options. This permits us to study the best/worst behaviour of the system. We generalise model-free reinforcement learning techniques to compute an optimal control strategy of an unknown BMDP in the limit. We present results of an implementation that demonstrate the practicality of the approach.

Omega-Regular Objectives in Model-Free Reinforcement Learning

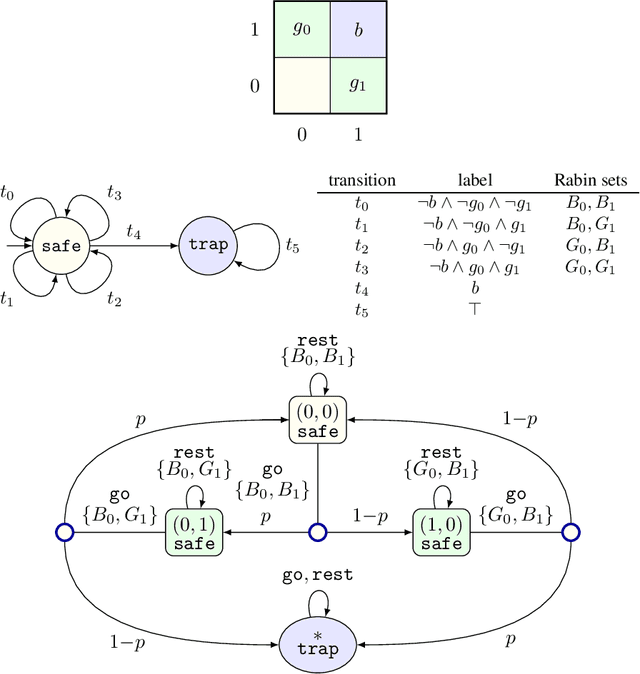
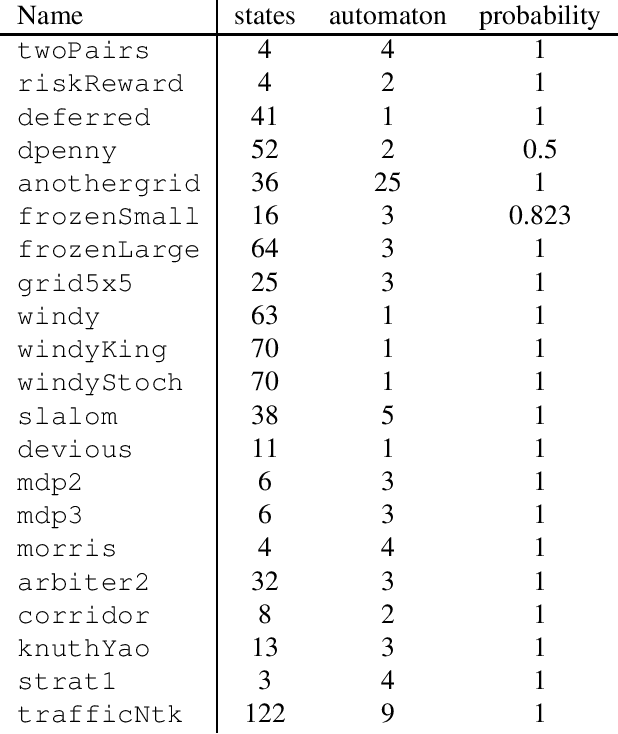
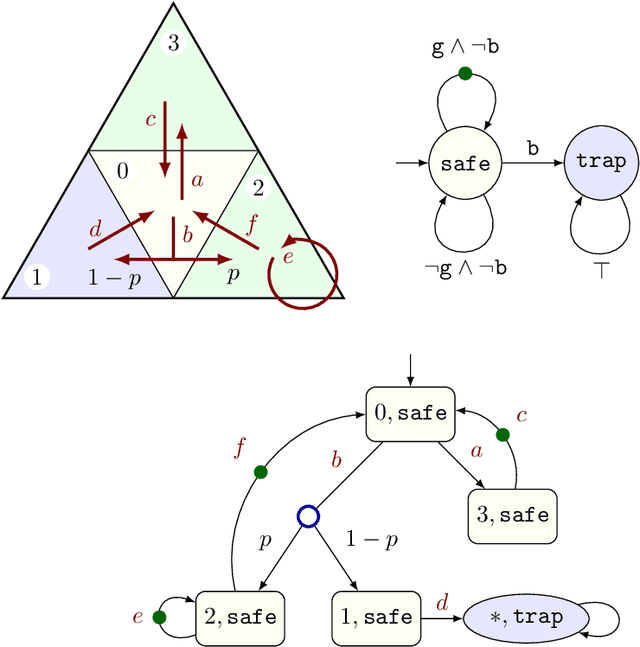
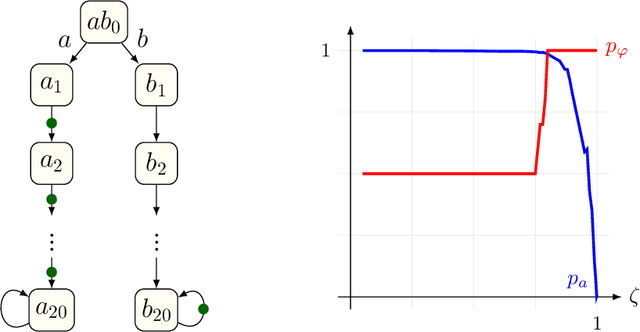
We provide the first solution for model-free reinforcement learning of {\omega}-regular objectives for Markov decision processes (MDPs). We present a constructive reduction from the almost-sure satisfaction of {\omega}-regular objectives to an almost- sure reachability problem and extend this technique to learning how to control an unknown model so that the chance of satisfying the objective is maximized. A key feature of our technique is the compilation of {\omega}-regular properties into limit- deterministic Buechi automata instead of the traditional Rabin automata; this choice sidesteps difficulties that have marred previous proposals. Our approach allows us to apply model-free, off-the-shelf reinforcement learning algorithms to compute optimal strategies from the observations of the MDP. We present an experimental evaluation of our technique on benchmark learning problems.