Sven Schewe
Good-for-MDP State Reduction for Stochastic LTL Planning
Nov 15, 2025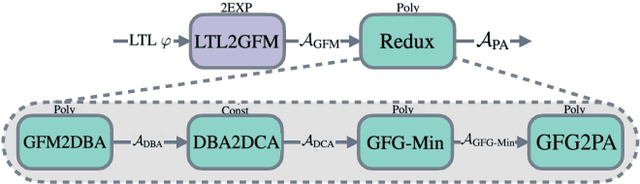
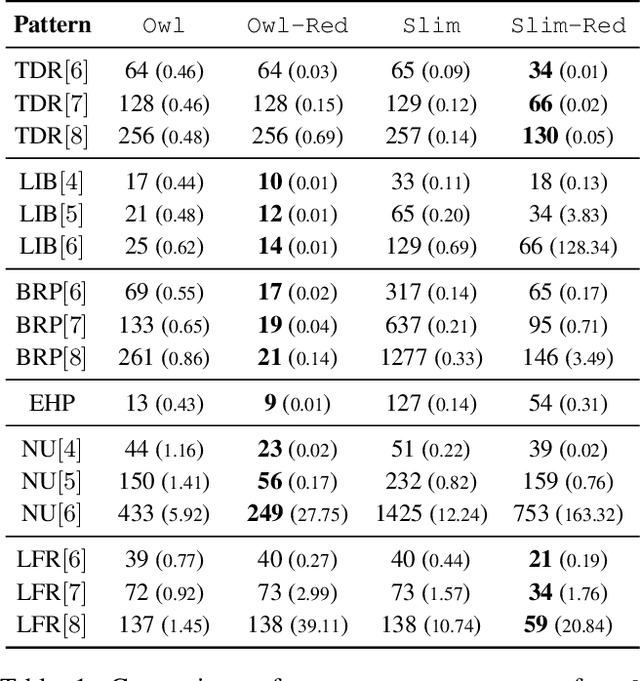
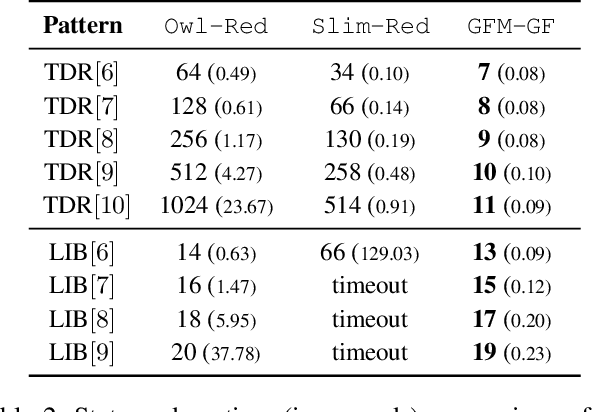
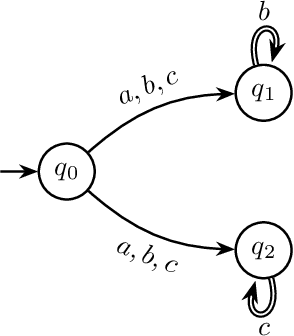
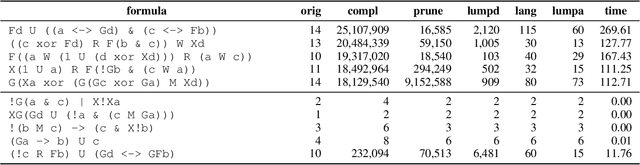
Abstract:We study stochastic planning problems in Markov Decision Processes (MDPs) with goals specified in Linear Temporal Logic (LTL). The state-of-the-art approach transforms LTL formulas into good-for-MDP (GFM) automata, which feature a restricted form of nondeterminism. These automata are then composed with the MDP, allowing the agent to resolve the nondeterminism during policy synthesis. A major factor affecting the scalability of this approach is the size of the generated automata. In this paper, we propose a novel GFM state-space reduction technique that significantly reduces the number of automata states. Our method employs a sophisticated chain of transformations, leveraging recent advances in good-for-games minimisation developed for adversarial settings. In addition to our theoretical contributions, we present empirical results demonstrating the practical effectiveness of our state-reduction technique. Furthermore, we introduce a direct construction method for formulas of the form $\mathsf{G}\mathsf{F}\varphi$, where $\varphi$ is a co-safety formula. This construction is provably single-exponential in the worst case, in contrast to the general doubly-exponential complexity. Our experiments confirm the scalability advantages of this specialised construction.
DFAMiner: Mining minimal separating DFAs from labelled samples
May 29, 2024Abstract:We propose DFAMiner, a passive learning tool for learning minimal separating deterministic finite automata (DFA) from a set of labelled samples. Separating automata are an interesting class of automata that occurs generally in regular model checking and has raised interest in foundational questions of parity game solving. We first propose a simple and linear-time algorithm that incrementally constructs a three-valued DFA (3DFA) from a set of labelled samples given in the usual lexicographical order. This 3DFA has accepting and rejecting states as well as don't-care states, so that it can exactly recognise the labelled examples. We then apply our tool to mining a minimal separating DFA for the labelled samples by minimising the constructed automata via a reduction to solving SAT problems. Empirical evaluation shows that our tool outperforms current state-of-the-art tools significantly on standard benchmarks for learning minimal separating DFAs from samples. Progress in the efficient construction of separating DFAs can also lead to finding the lower bound of parity game solving, where we show that DFAMiner can create optimal separating automata for simple languages with up to 7 colours. Future improvements might offer inroads to better data structures.
Omega-Regular Decision Processes
Dec 14, 2023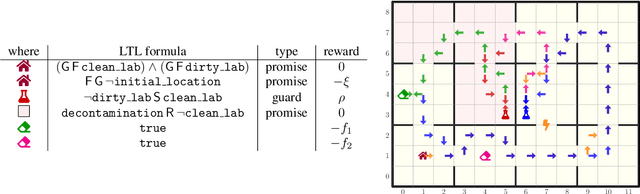

Abstract:Regular decision processes (RDPs) are a subclass of non-Markovian decision processes where the transition and reward functions are guarded by some regular property of the past (a lookback). While RDPs enable intuitive and succinct representation of non-Markovian decision processes, their expressive power coincides with finite-state Markov decision processes (MDPs). We introduce omega-regular decision processes (ODPs) where the non-Markovian aspect of the transition and reward functions are extended to an omega-regular lookahead over the system evolution. Semantically, these lookaheads can be considered as promises made by the decision maker or the learning agent about her future behavior. In particular, we assume that, if the promised lookaheads are not met, then the payoff to the decision maker is $\bot$ (least desirable payoff), overriding any rewards collected by the decision maker. We enable optimization and learning for ODPs under the discounted-reward objective by reducing them to lexicographic optimization and learning over finite MDPs. We present experimental results demonstrating the effectiveness of the proposed reduction.
Omega-Regular Reward Machines
Aug 14, 2023Abstract:Reinforcement learning (RL) is a powerful approach for training agents to perform tasks, but designing an appropriate reward mechanism is critical to its success. However, in many cases, the complexity of the learning objectives goes beyond the capabilities of the Markovian assumption, necessitating a more sophisticated reward mechanism. Reward machines and omega-regular languages are two formalisms used to express non-Markovian rewards for quantitative and qualitative objectives, respectively. This paper introduces omega-regular reward machines, which integrate reward machines with omega-regular languages to enable an expressive and effective reward mechanism for RL. We present a model-free RL algorithm to compute epsilon-optimal strategies against omega-egular reward machines and evaluate the effectiveness of the proposed algorithm through experiments.
Recursive Reinforcement Learning
Jun 23, 2022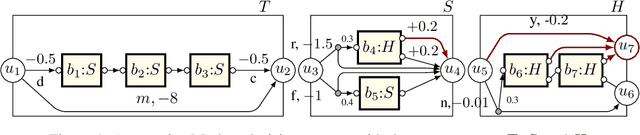


Abstract:Recursion is the fundamental paradigm to finitely describe potentially infinite objects. As state-of-the-art reinforcement learning (RL) algorithms cannot directly reason about recursion, they must rely on the practitioner's ingenuity in designing a suitable "flat" representation of the environment. The resulting manual feature constructions and approximations are cumbersome and error-prone; their lack of transparency hampers scalability. To overcome these challenges, we develop RL algorithms capable of computing optimal policies in environments described as a collection of Markov decision processes (MDPs) that can recursively invoke one another. Each constituent MDP is characterized by several entry and exit points that correspond to input and output values of these invocations. These recursive MDPs (or RMDPs) are expressively equivalent to probabilistic pushdown systems (with call-stack playing the role of the pushdown stack), and can model probabilistic programs with recursive procedural calls. We introduce Recursive Q-learning -- a model-free RL algorithm for RMDPs -- and prove that it converges for finite, single-exit and deterministic multi-exit RMDPs under mild assumptions.
Alternating Good-for-MDP Automata
May 06, 2022
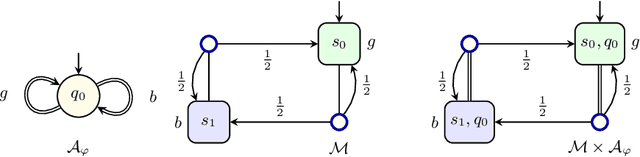
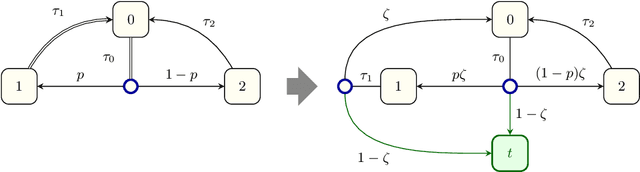
Abstract:When omega-regular objectives were first proposed in model-free reinforcement learning (RL) for controlling MDPs, deterministic Rabin automata were used in an attempt to provide a direct translation from their transitions to scalar values. While these translations failed, it has turned out that it is possible to repair them by using good-for-MDPs (GFM) B\"uchi automata instead. These are nondeterministic B\"uchi automata with a restricted type of nondeterminism, albeit not as restricted as in good-for-games automata. Indeed, deterministic Rabin automata have a pretty straightforward translation to such GFM automata, which is bi-linear in the number of states and pairs. Interestingly, the same cannot be said for deterministic Streett automata: a translation to nondeterministic Rabin or B\"uchi automata comes at an exponential cost, even without requiring the target automaton to be good-for-MDPs. Do we have to pay more than that to obtain a good-for-MDP automaton? The surprising answer is that we have to pay significantly less when we instead expand the good-for-MDP property to alternating automata: like the nondeterministic GFM automata obtained from deterministic Rabin automata, the alternating good-for-MDP automata we produce from deterministic Streett automata are bi-linear in the the size of the deterministic automaton and its index, and can therefore be exponentially more succinct than minimal nondeterministic B\"uchi automata.
Enhancing Adversarial Training with Second-Order Statistics of Weights
Mar 11, 2022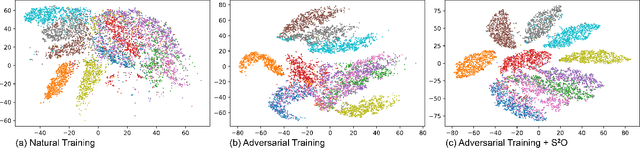
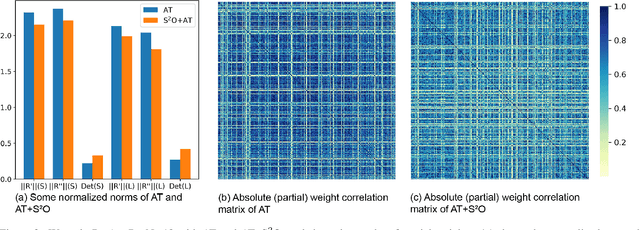
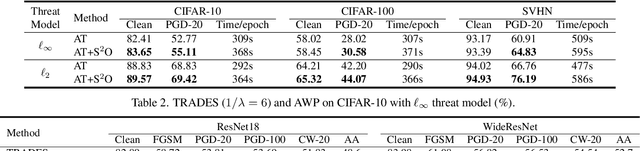
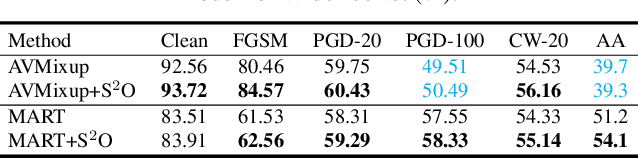
Abstract:Adversarial training has been shown to be one of the most effective approaches to improve the robustness of deep neural networks. It is formalized as a min-max optimization over model weights and adversarial perturbations, where the weights can be optimized through gradient descent methods like SGD. In this paper, we show that treating model weights as random variables allows for enhancing adversarial training through \textbf{S}econd-Order \textbf{S}tatistics \textbf{O}ptimization (S$^2$O) with respect to the weights. By relaxing a common (but unrealistic) assumption of previous PAC-Bayesian frameworks that all weights are statistically independent, we derive an improved PAC-Bayesian adversarial generalization bound, which suggests that optimizing second-order statistics of weights can effectively tighten the bound. In addition to this theoretical insight, we conduct an extensive set of experiments, which show that S$^2$O not only improves the robustness and generalization of the trained neural networks when used in isolation, but also integrates easily in state-of-the-art adversarial training techniques like TRADES, AWP, MART, and AVMixup, leading to a measurable improvement of these techniques. The code is available at \url{https://github.com/Alexkael/S2O}.
Weight Expansion: A New Perspective on Dropout and Generalization
Jan 23, 2022

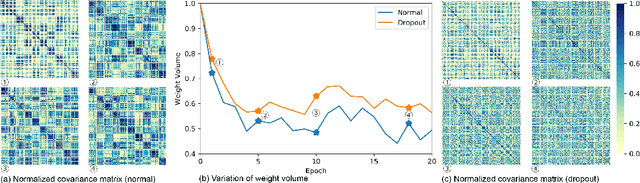

Abstract:While dropout is known to be a successful regularization technique, insights into the mechanisms that lead to this success are still lacking. We introduce the concept of \emph{weight expansion}, an increase in the signed volume of a parallelotope spanned by the column or row vectors of the weight covariance matrix, and show that weight expansion is an effective means of increasing the generalization in a PAC-Bayesian setting. We provide a theoretical argument that dropout leads to weight expansion and extensive empirical support for the correlation between dropout and weight expansion. To support our hypothesis that weight expansion can be regarded as an \emph{indicator} of the enhanced generalization capability endowed by dropout, and not just as a mere by-product, we have studied other methods that achieve weight expansion (resp.\ contraction), and found that they generally lead to an increased (resp.\ decreased) generalization ability. This suggests that dropout is an attractive regularizer, because it is a computationally cheap method for obtaining weight expansion. This insight justifies the role of dropout as a regularizer, while paving the way for identifying regularizers that promise improved generalization through weight expansion.
Reliability Assessment and Safety Arguments for Machine Learning Components in Assuring Learning-Enabled Autonomous Systems
Nov 30, 2021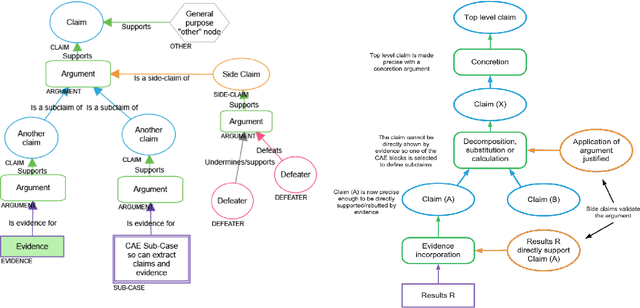

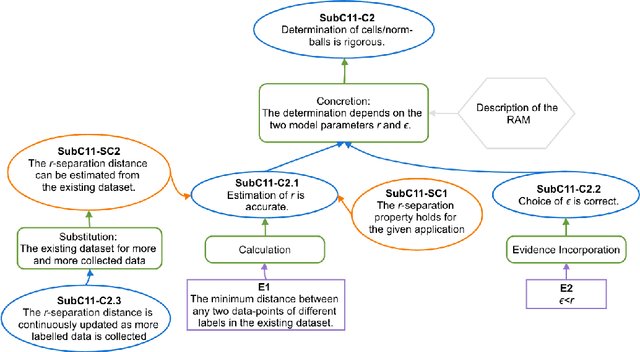
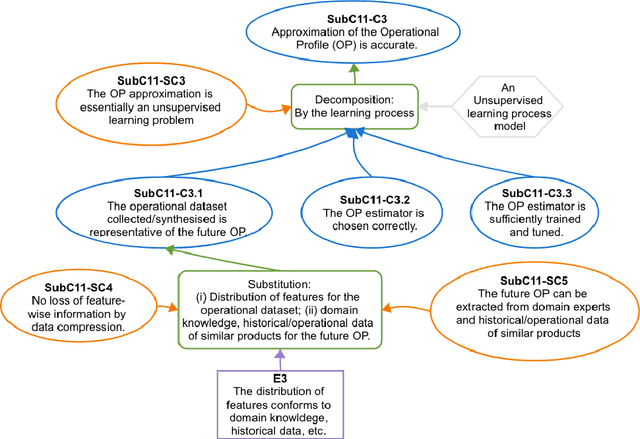
Abstract:The increasing use of Machine Learning (ML) components embedded in autonomous systems -- so-called Learning-Enabled Systems (LES) -- has resulted in the pressing need to assure their functional safety. As for traditional functional safety, the emerging consensus within both, industry and academia, is to use assurance cases for this purpose. Typically assurance cases support claims of reliability in support of safety, and can be viewed as a structured way of organising arguments and evidence generated from safety analysis and reliability modelling activities. While such assurance activities are traditionally guided by consensus-based standards developed from vast engineering experience, LES pose new challenges in safety-critical application due to the characteristics and design of ML models. In this article, we first present an overall assurance framework for LES with an emphasis on quantitative aspects, e.g., breaking down system-level safety targets to component-level requirements and supporting claims stated in reliability metrics. We then introduce a novel model-agnostic Reliability Assessment Model (RAM) for ML classifiers that utilises the operational profile and robustness verification evidence. We discuss the model assumptions and the inherent challenges of assessing ML reliability uncovered by our RAM and propose practical solutions. Probabilistic safety arguments at the lower ML component-level are also developed based on the RAM. Finally, to evaluate and demonstrate our methods, we not only conduct experiments on synthetic/benchmark datasets but also demonstrate the scope of our methods with a comprehensive case study on Autonomous Underwater Vehicles in simulation.
Mungojerrie: Reinforcement Learning of Linear-Time Objectives
Jun 18, 2021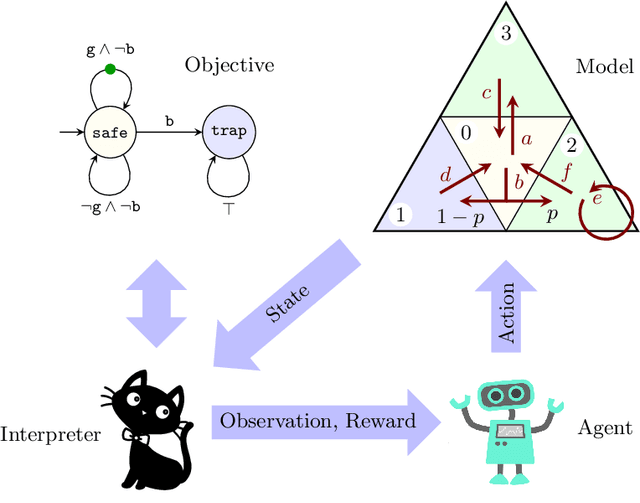

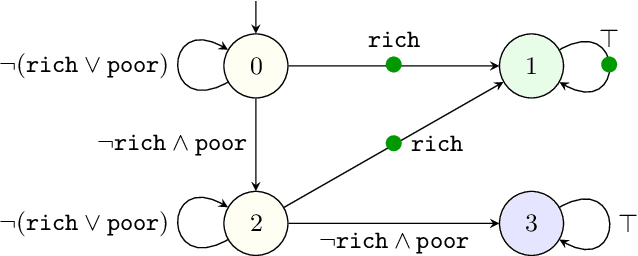

Abstract:Reinforcement learning synthesizes controllers without prior knowledge of the system. At each timestep, a reward is given. The controllers optimize the discounted sum of these rewards. Applying this class of algorithms requires designing a reward scheme, which is typically done manually. The designer must ensure that their intent is accurately captured. This may not be trivial, and is prone to error. An alternative to this manual programming, akin to programming directly in assembly, is to specify the objective in a formal language and have it "compiled" to a reward scheme. Mungojerrie (https://plv.colorado.edu/mungojerrie/) is a tool for testing reward schemes for $\omega$-regular objectives on finite models. The tool contains reinforcement learning algorithms and a probabilistic model checker. Mungojerrie supports models specified in PRISM and $\omega$-automata specified in HOA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge