Formal Controller Synthesis for Continuous-Space MDPs via Model-Free Reinforcement Learning

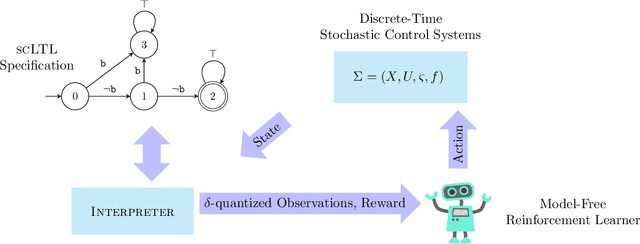
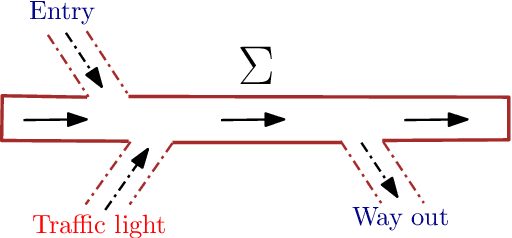
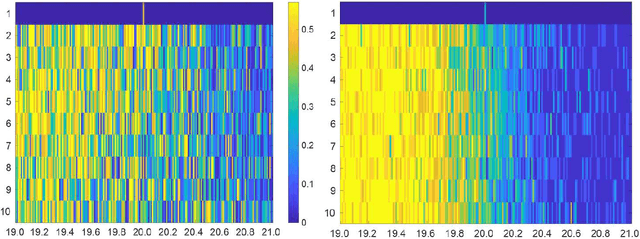
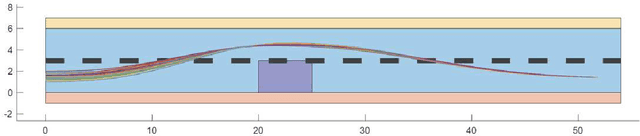
A novel reinforcement learning scheme to synthesize policies for continuous-space Markov decision processes (MDPs) is proposed. This scheme enables one to apply model-free, off-the-shelf reinforcement learning algorithms for finite MDPs to compute optimal strategies for the corresponding continuous-space MDPs without explicitly constructing the finite-state abstraction. The proposed approach is based on abstracting the system with a finite MDP (without constructing it explicitly) with unknown transition probabilities, synthesizing strategies over the abstract MDP, and then mapping the results back over the concrete continuous-space MDP with approximate optimality guarantees. The properties of interest for the system belong to a fragment of linear temporal logic, known as syntactically co-safe linear temporal logic (scLTL), and the synthesis requirement is to maximize the probability of satisfaction within a given bounded time horizon. A key contribution of the paper is to leverage the classical convergence results for reinforcement learning on finite MDPs and provide control strategies maximizing the probability of satisfaction over unknown, continuous-space MDPs while providing probabilistic closeness guarantees. Automata-based reward functions are often sparse; we present a novel potential-based reward shaping technique to produce dense rewards to speed up learning. The effectiveness of the proposed approach is demonstrated by applying it to three physical benchmarks concerning the regulation of a room's temperature, control of a road traffic cell, and of a 7-dimensional nonlinear model of a BMW 320i car.