LUCID: Learning-Enabled Uncertainty-Aware Certification of Stochastic Dynamical Systems

Ensuring the safety of AI-enabled systems, particularly in high-stakes domains such as autonomous driving and healthcare, has become increasingly critical. Traditional formal verification tools fall short when faced with systems that embed both opaque, black-box AI components and complex stochastic dynamics. To address these challenges, we introduce LUCID (Learning-enabled Uncertainty-aware Certification of stochastIc Dynamical systems), a verification engine for certifying safety of black-box stochastic dynamical systems from a finite dataset of random state transitions. As such, LUCID is the first known tool capable of establishing quantified safety guarantees for such systems. Thanks to its modular architecture and extensive documentation, LUCID is designed for easy extensibility. LUCID employs a data-driven methodology rooted in control barrier certificates, which are learned directly from system transition data, to ensure formal safety guarantees. We use conditional mean embeddings to embed data into a reproducing kernel Hilbert space (RKHS), where an RKHS ambiguity set is constructed that can be inflated to robustify the result to out-of-distribution behavior. A key innovation within LUCID is its use of a finite Fourier kernel expansion to reformulate a semi-infinite non-convex optimization problem into a tractable linear program. The resulting spectral barrier allows us to leverage the fast Fourier transform to generate the relaxed problem efficiently, offering a scalable yet distributionally robust framework for verifying safety. LUCID thus offers a robust and efficient verification framework, able to handle the complexities of modern black-box systems while providing formal guarantees of safety. These unique capabilities are demonstrated on challenging benchmarks.

Data-Driven Distributionally Robust Safety Verification Using Barrier Certificates and Conditional Mean Embeddings

Algorithmic verification of realistic systems to satisfy safety and other temporal requirements has suffered from poor scalability of the employed formal approaches. To design systems with rigorous guarantees, many approaches still rely on exact models of the underlying systems. Since this assumption can rarely be met in practice, models have to be inferred from measurement data or are bypassed completely. Whilst former usually requires the model structure to be known a-priori and immense amounts of data to be available, latter gives rise to a plethora of restrictive mathematical assumptions about the unknown dynamics. In a pursuit of developing scalable formal verification algorithms without shifting the problem to unrealistic assumptions, we employ the concept of barrier certificates, which can guarantee safety of the system, and learn the certificate directly from a compact set of system trajectories. We use conditional mean embeddings to embed data from the system into a reproducing kernel Hilbert space (RKHS) and construct an RKHS ambiguity set that can be inflated to robustify the result w.r.t. a set of plausible transition kernels. We show how to solve the resulting program efficiently using sum-of-squares optimization and a Gaussian process envelope. Our approach lifts the need for restrictive assumptions on the system dynamics and uncertainty, and suggests an improvement in the sample complexity of verifying the safety of a system on a tested case study compared to a state-of-the-art approach.

Multi-Objective Physics-Guided Recurrent Neural Networks for Identifying Non-Autonomous Dynamical Systems

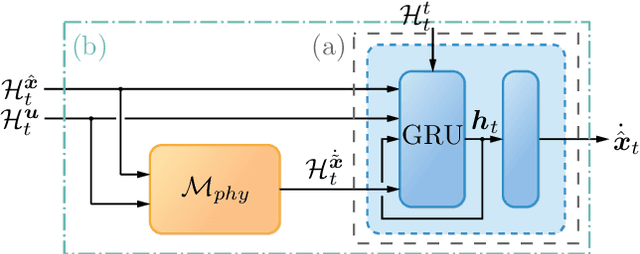
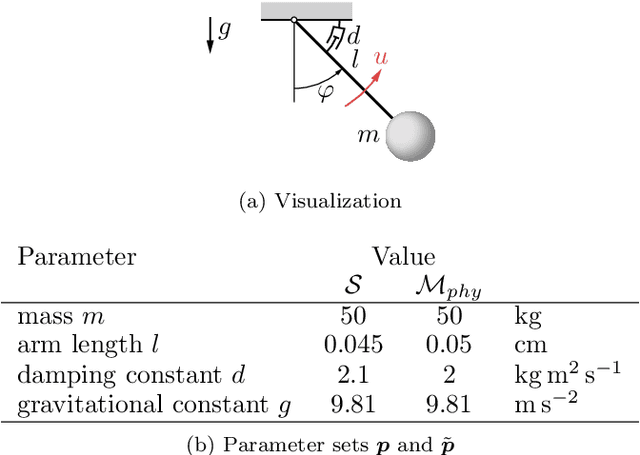
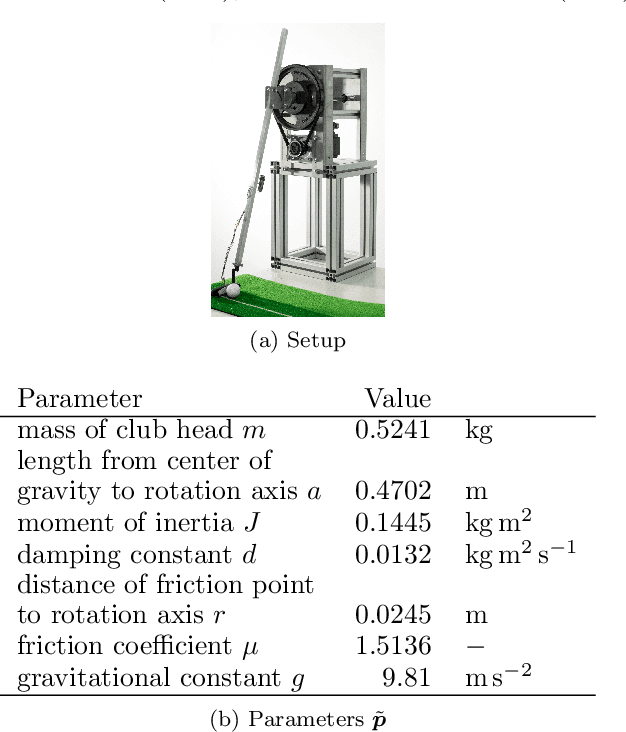
While trade-offs between modeling effort and model accuracy remain a major concern with system identification, resorting to data-driven methods often leads to a complete disregard for physical plausibility. To address this issue, we propose a physics-guided hybrid approach for modeling non-autonomous systems under control. Starting from a traditional physics-based model, this is extended by a recurrent neural network and trained using a sophisticated multi-objective strategy yielding physically plausible models. While purely data-driven methods fail to produce satisfying results, experiments conducted on real data reveal substantial accuracy improvements by our approach compared to a physics-based model.