Approximating a Laplacian Prior for Joint State and Model Estimation within an UKF

A major challenge in state estimation with model-based observers are low-quality models that lack of relevant dynamics. We address this issue by simultaneously estimating the system's states and its model uncertainties by a square root UKF. Concretely, we extend the state by the parameter vector of a linear combination containing suitable functions that approximate the lacking dynamics. Presuming that only a few dynamical terms are relevant, the parameter vector is claimed to be sparse. In Bayesian setting, properties like sparsity are expressed by a prior distribution. One common choice for sparsity is a Laplace distribution. However, due to some disadvantages of a Laplacian prior, the regularized horseshoe distribution, a Gaussian that approximately features sparsity, is applied. Results exhibit small estimation errors with model improvements detected by an automated model reduction technique.

Estimating States and Model Uncertainties Jointly by a Sparsity Promoting UKF

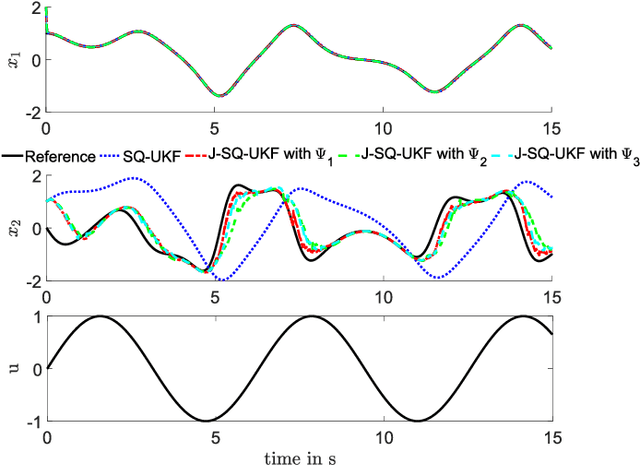
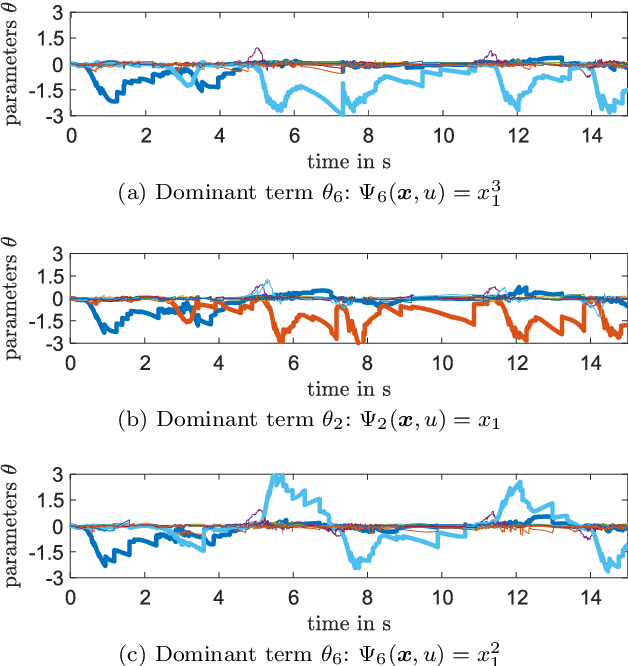
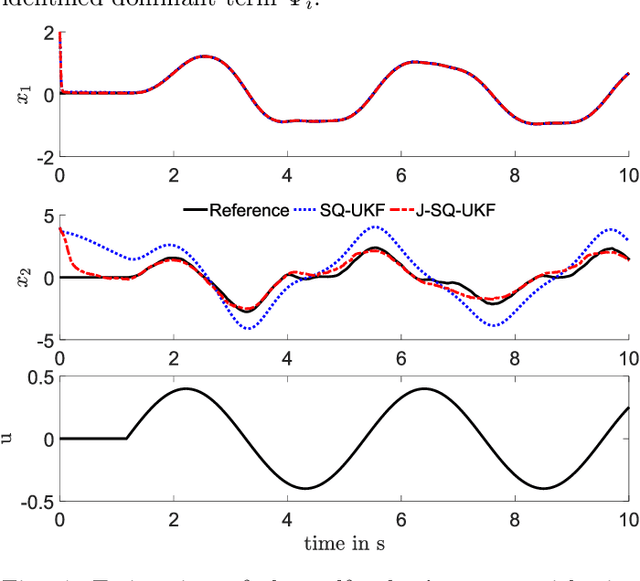
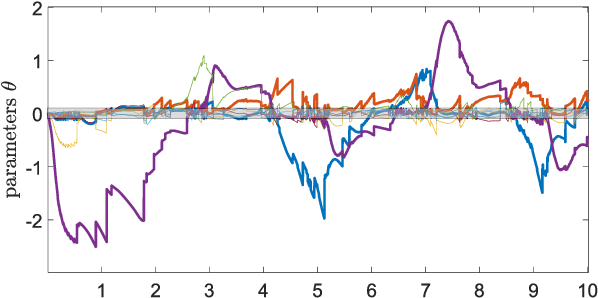
State estimation when only a partial model of a considered system is available remains a major challenge in many engineering fields. This work proposes a joint, square-root unscented Kalman filter to estimate states and model uncertainties simultaneously by linear combinations of physics-motivated library functions. Using a sparsity promoting approach, a selection of those linear combinations is chosen and thus an interpretable model can be extracted. Results indicate a small estimation error compared to a traditional square-root unscented Kalman filter and exhibit the enhancement of physically meaningful models.

Multi-Objective Physics-Guided Recurrent Neural Networks for Identifying Non-Autonomous Dynamical Systems

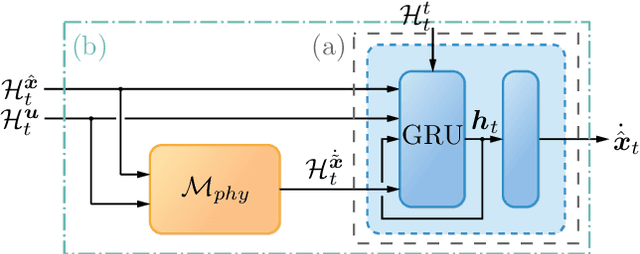
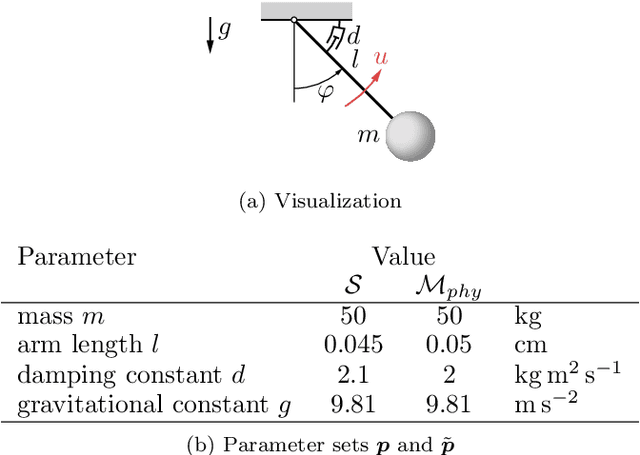
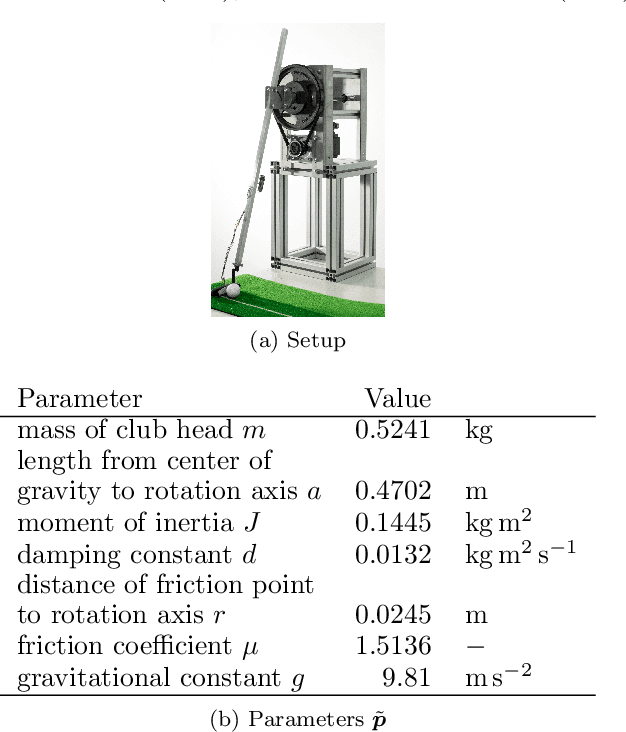
While trade-offs between modeling effort and model accuracy remain a major concern with system identification, resorting to data-driven methods often leads to a complete disregard for physical plausibility. To address this issue, we propose a physics-guided hybrid approach for modeling non-autonomous systems under control. Starting from a traditional physics-based model, this is extended by a recurrent neural network and trained using a sophisticated multi-objective strategy yielding physically plausible models. While purely data-driven methods fail to produce satisfying results, experiments conducted on real data reveal substantial accuracy improvements by our approach compared to a physics-based model.