Approximating a Laplacian Prior for Joint State and Model Estimation within an UKF

A major challenge in state estimation with model-based observers are low-quality models that lack of relevant dynamics. We address this issue by simultaneously estimating the system's states and its model uncertainties by a square root UKF. Concretely, we extend the state by the parameter vector of a linear combination containing suitable functions that approximate the lacking dynamics. Presuming that only a few dynamical terms are relevant, the parameter vector is claimed to be sparse. In Bayesian setting, properties like sparsity are expressed by a prior distribution. One common choice for sparsity is a Laplace distribution. However, due to some disadvantages of a Laplacian prior, the regularized horseshoe distribution, a Gaussian that approximately features sparsity, is applied. Results exhibit small estimation errors with model improvements detected by an automated model reduction technique.

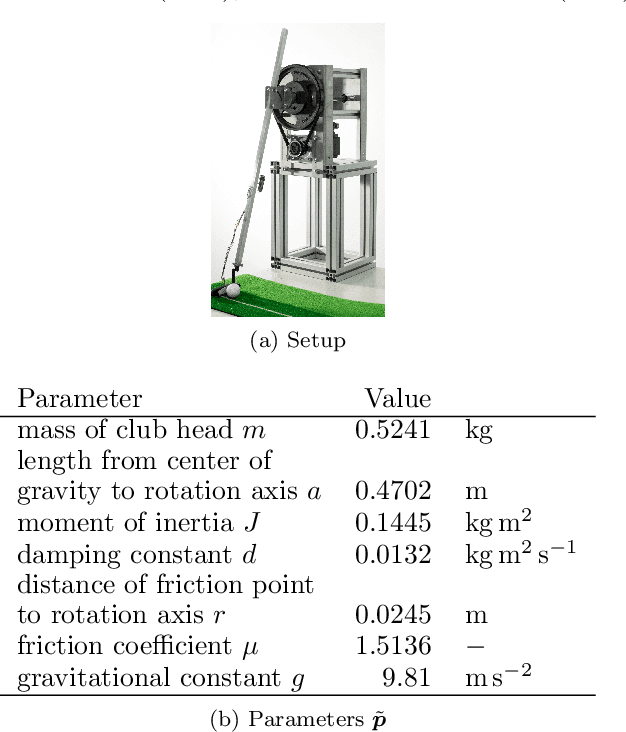
Autonomous Golf Putting with Data-Driven and Physics-Based Methods

We are developing a self-learning mechatronic golf robot using combined data-driven and physics-based methods, to have the robot autonomously learn to putt the ball from an arbitrary point on the green. Apart from the mechatronic control design of the robot, this task is accomplished by a camera system with image recognition and a neural network for predicting the stroke velocity vector required for a successful hole-in-one. To minimize the number of time-consuming interactions with the real system, the neural network is pretrained by evaluating basic physical laws on a model, which approximates the golf ball dynamics on the green surface in a data-driven manner. Thus, we demonstrate the synergetic combination of data-driven and physics-based methods on the golf robot as a mechatronic example system.

Estimating States and Model Uncertainties Jointly by a Sparsity Promoting UKF

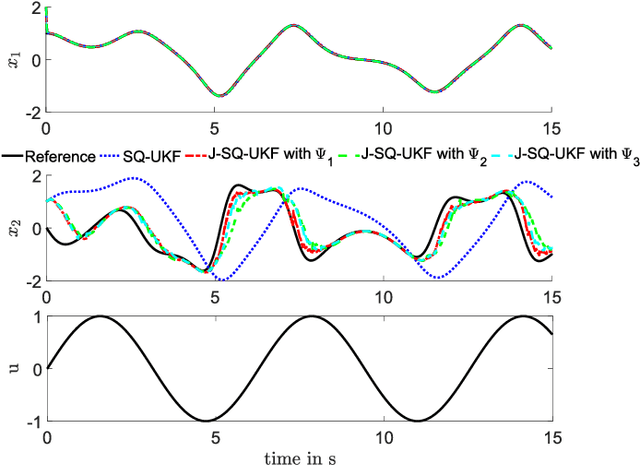
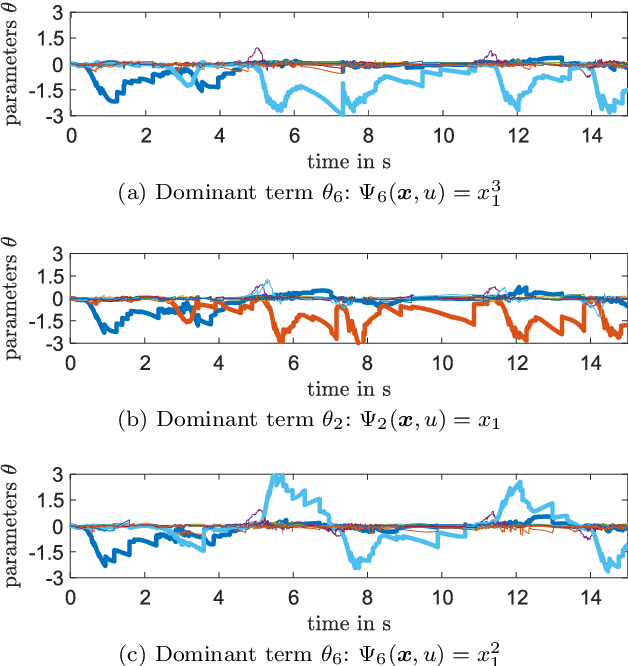
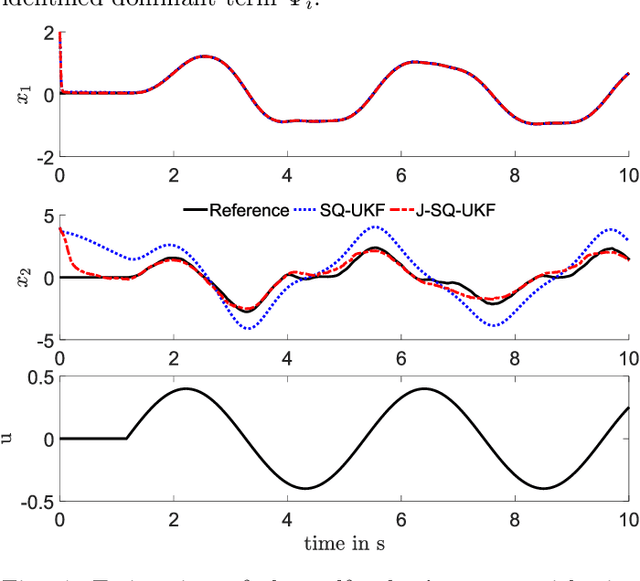
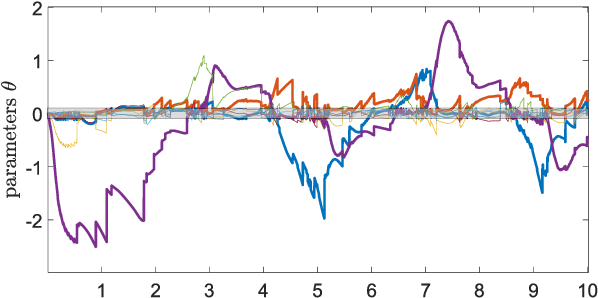
State estimation when only a partial model of a considered system is available remains a major challenge in many engineering fields. This work proposes a joint, square-root unscented Kalman filter to estimate states and model uncertainties simultaneously by linear combinations of physics-motivated library functions. Using a sparsity promoting approach, a selection of those linear combinations is chosen and thus an interpretable model can be extracted. Results indicate a small estimation error compared to a traditional square-root unscented Kalman filter and exhibit the enhancement of physically meaningful models.

Multi-Objective Physics-Guided Recurrent Neural Networks for Identifying Non-Autonomous Dynamical Systems

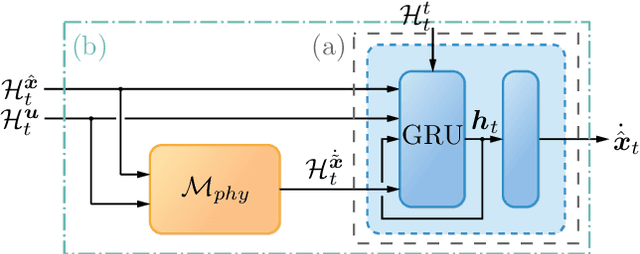
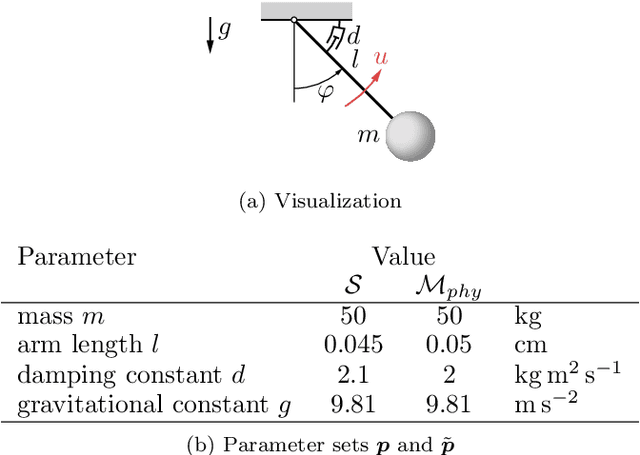
While trade-offs between modeling effort and model accuracy remain a major concern with system identification, resorting to data-driven methods often leads to a complete disregard for physical plausibility. To address this issue, we propose a physics-guided hybrid approach for modeling non-autonomous systems under control. Starting from a traditional physics-based model, this is extended by a recurrent neural network and trained using a sophisticated multi-objective strategy yielding physically plausible models. While purely data-driven methods fail to produce satisfying results, experiments conducted on real data reveal substantial accuracy improvements by our approach compared to a physics-based model.