Verifiably Robust Conformal Prediction

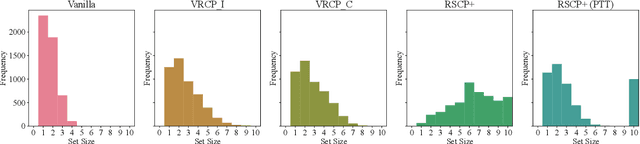
Conformal Prediction (CP) is a popular uncertainty quantification method that provides distribution-free, statistically valid prediction sets, assuming that training and test data are exchangeable. In such a case, CP's prediction sets are guaranteed to cover the (unknown) true test output with a user-specified probability. Nevertheless, this guarantee is violated when the data is subjected to adversarial attacks, which often result in a significant loss of coverage. Recently, several approaches have been put forward to recover CP guarantees in this setting. These approaches leverage variations of randomised smoothing to produce conservative sets which account for the effect of the adversarial perturbations. They are, however, limited in that they only support $\ell^2$-bounded perturbations and classification tasks. This paper introduces \emph{VRCP (Verifiably Robust Conformal Prediction)}, a new framework that leverages recent neural network verification methods to recover coverage guarantees under adversarial attacks. Our VRCP method is the first to support perturbations bounded by arbitrary norms including $\ell^1$, $\ell^2$, and $\ell^\infty$, as well as regression tasks. We evaluate and compare our approach on image classification tasks (CIFAR10, CIFAR100, and TinyImageNet) and regression tasks for deep reinforcement learning environments. In every case, VRCP achieves above nominal coverage and yields significantly more efficient and informative prediction regions than the SotA.

Conformal Off-Policy Prediction for Multi-Agent Systems

Off-Policy Prediction (OPP), i.e., predicting the outcomes of a target policy using only data collected under a nominal (behavioural) policy, is a paramount problem in data-driven analysis of safety-critical systems where the deployment of a new policy may be unsafe. To achieve dependable off-policy predictions, recent work on Conformal Off-Policy Prediction (COPP) leverage the conformal prediction framework to derive prediction regions with probabilistic guarantees under the target process. Existing COPP methods can account for the distribution shifts induced by policy switching, but are limited to single-agent systems and scalar outcomes (e.g., rewards). In this work, we introduce MA-COPP, the first conformal prediction method to solve OPP problems involving multi-agent systems, deriving joint prediction regions for all agents' trajectories when one or more "ego" agents change their policies. Unlike the single-agent scenario, this setting introduces higher complexity as the distribution shifts affect predictions for all agents, not just the ego agents, and the prediction task involves full multi-dimensional trajectories, not just reward values. A key contribution of MA-COPP is to avoid enumeration or exhaustive search of the output space of agent trajectories, which is instead required by existing COPP methods to construct the prediction region. We achieve this by showing that an over-approximation of the true JPR can be constructed, without enumeration, from the maximum density ratio of the JPR trajectories. We evaluate the effectiveness of MA-COPP in multi-agent systems from the PettingZoo library and the F1TENTH autonomous racing environment, achieving nominal coverage in higher dimensions and various shift settings.