MotionPRO: Exploring the Role of Pressure in Human MoCap and Beyond

Existing human Motion Capture (MoCap) methods mostly focus on the visual similarity while neglecting the physical plausibility. As a result, downstream tasks such as driving virtual human in 3D scene or humanoid robots in real world suffer from issues such as timing drift and jitter, spatial problems like sliding and penetration, and poor global trajectory accuracy. In this paper, we revisit human MoCap from the perspective of interaction between human body and physical world by exploring the role of pressure. Firstly, we construct a large-scale human Motion capture dataset with Pressure, RGB and Optical sensors (named MotionPRO), which comprises 70 volunteers performing 400 types of motion, encompassing a total of 12.4M pose frames. Secondly, we examine both the necessity and effectiveness of the pressure signal through two challenging tasks: (1) pose and trajectory estimation based solely on pressure: We propose a network that incorporates a small kernel decoder and a long-short-term attention module, and proof that pressure could provide accurate global trajectory and plausible lower body pose. (2) pose and trajectory estimation by fusing pressure and RGB: We impose constraints on orthographic similarity along the camera axis and whole-body contact along the vertical axis to enhance the cross-attention strategy to fuse pressure and RGB feature maps. Experiments demonstrate that fusing pressure with RGB features not only significantly improves performance in terms of objective metrics, but also plausibly drives virtual humans (SMPL) in 3D scene. Furthermore, we demonstrate that incorporating physical perception enables humanoid robots to perform more precise and stable actions, which is highly beneficial for the development of embodied artificial intelligence. Project page is available at: https://nju-cite-mocaphumanoid.github.io/MotionPRO/

Capacity-Aware Inference: Mitigating the Straggler Effect in Mixture of Experts

The Mixture of Experts (MoE) is an effective architecture for scaling large language models by leveraging sparse expert activation, optimizing the trade-off between performance and efficiency. However, under expert parallelism, MoE suffers from inference inefficiencies due to imbalanced token-to-expert assignment, where some experts are overloaded while others remain underutilized. This imbalance leads to poor resource utilization and increased latency, as the most burdened expert dictates the overall delay, a phenomenon we define as the \textbf{\textit{Straggler Effect}}. To mitigate this, we propose Capacity-Aware Inference, including two key techniques: (1) \textbf{\textit{Capacity-Aware Token Drop}}, which discards overloaded tokens to regulate the maximum latency of MoE, and (2) \textbf{\textit{Capacity-Aware Token Reroute}}, which reallocates overflowed tokens to underutilized experts, balancing the token distribution. These techniques collectively optimize both high-load and low-load expert utilization, leading to a more efficient MoE inference pipeline. Extensive experiments demonstrate the effectiveness of our methods, showing significant improvements in inference efficiency, e.g., 0.2\% average performance increase and a 1.94$\times$ inference speedup on Mixtral-8$\times$7B-Instruct.

Defect Detection Network In PCB Circuit Devices Based on GAN Enhanced YOLOv11

This study proposes an advanced method for surface defect detection in printed circuit boards (PCBs) using an improved YOLOv11 model enhanced with a generative adversarial network (GAN). The approach focuses on identifying six common defect types: missing hole, rat bite, open circuit, short circuit, burr, and virtual welding. By employing GAN to generate synthetic defect images, the dataset is augmented with diverse and realistic patterns, improving the model's ability to generalize, particularly for complex and infrequent defects like burrs. The enhanced YOLOv11 model is evaluated on a PCB defect dataset, demonstrating significant improvements in accuracy, recall, and robustness, especially when dealing with defects in complex environments or small targets. This research contributes to the broader field of electronic design automation (EDA), where efficient defect detection is a crucial step in ensuring high-quality PCB manufacturing. By integrating advanced deep learning techniques, this approach enhances the automation and precision of defect detection, reducing reliance on manual inspection and accelerating design-to-production workflows. The findings underscore the importance of incorporating GAN-based data augmentation and optimized detection architectures in EDA processes, providing valuable insights for improving reliability and efficiency in PCB defect detection within industrial applications.

Distilling Calibration via Conformalized Credal Inference

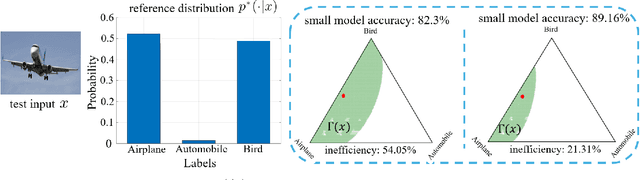
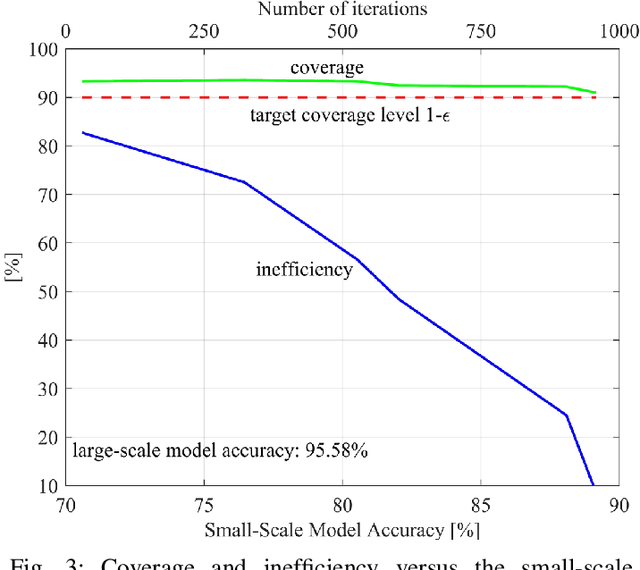
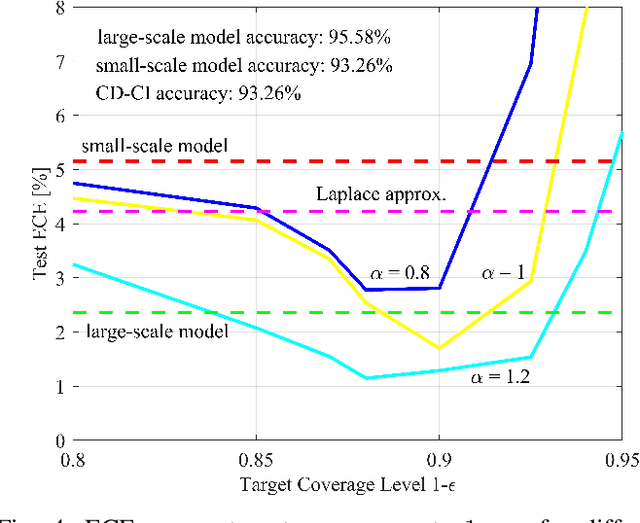
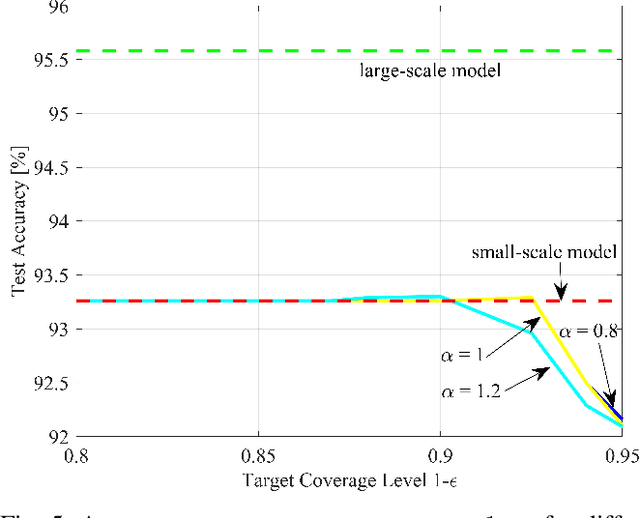
Deploying artificial intelligence (AI) models on edge devices involves a delicate balance between meeting stringent complexity constraints, such as limited memory and energy resources, and ensuring reliable performance in sensitive decision-making tasks. One way to enhance reliability is through uncertainty quantification via Bayesian inference. This approach, however, typically necessitates maintaining and running multiple models in an ensemble, which may exceed the computational limits of edge devices. This paper introduces a low-complexity methodology to address this challenge by distilling calibration information from a more complex model. In an offline phase, predictive probabilities generated by a high-complexity cloud-based model are leveraged to determine a threshold based on the typical divergence between the cloud and edge models. At run time, this threshold is used to construct credal sets -- ranges of predictive probabilities that are guaranteed, with a user-selected confidence level, to include the predictions of the cloud model. The credal sets are obtained through thresholding of a divergence measure in the simplex of predictive probabilities. Experiments on visual and language tasks demonstrate that the proposed approach, termed Conformalized Distillation for Credal Inference (CD-CI), significantly improves calibration performance compared to low-complexity Bayesian methods, such as Laplace approximation, making it a practical and efficient solution for edge AI deployments.

Partial Experts Checkpoint: Efficient Fault Tolerance for Sparse Mixture-of-Experts Model Training

As large language models continue to scale up, the imperative for fault tolerance in distributed deep learning systems intensifies, becoming a focal area of AI infrastructure research. Checkpoint has emerged as the predominant fault tolerance strategy, with extensive studies dedicated to optimizing its efficiency. However, the advent of the sparse Mixture-of-Experts (MoE) model presents new challenges for traditional checkpoint techniques due to the substantial increase in model size, despite comparable computational demands to dense models. Breaking new ground in the realm of efficient fault tolerance for MoE model training, we introduce a novel Partial Experts Checkpoint (PEC) mechanism alongside a corresponding PEC fault-tolerant system. Our approach strategically checkpoints a selected subset of experts, thereby significantly reducing the checkpoint size for MoE models to a level comparable with that of dense models. The empirical analysis on our 8-expert GPT-MoE model demonstrates that the proposed PEC approach facilitates a substantial 54.2% decrease in the size of non-redundant checkpoint (no data-parallel duplication), without compromising the final model quality. Moreover, our PEC fault-tolerant system achieves a 76.9% reduction in checkpoint workload per data-parallel distributed rank, thereby correspondingly diminishing the checkpointing time and facilitating complete overlap with the training process.

A Survey on Mixture of Experts

Large language models (LLMs) have garnered unprecedented advancements across diverse fields, ranging from natural language processing to computer vision and beyond. The prowess of LLMs is underpinned by their substantial model size, extensive and diverse datasets, and the vast computational power harnessed during training, all of which contribute to the emergent abilities of LLMs (e.g., in-context learning) that are not present in small models. Within this context, the mixture of experts (MoE) has emerged as an effective method for substantially scaling up model capacity with minimal computation overhead, gaining significant attention from academia and industry. Despite its growing prevalence, there lacks a systematic and comprehensive review of the literature on MoE. This survey seeks to bridge that gap, serving as an essential resource for researchers delving into the intricacies of MoE. We first briefly introduce the structure of the MoE layer, followed by proposing a new taxonomy of MoE. Next, we overview the core designs for various MoE models including both algorithmic and systemic aspects, alongside collections of available open-source implementations, hyperparameter configurations and empirical evaluations. Furthermore, we delineate the multifaceted applications of MoE in practice, and outline some potential directions for future research. To facilitate ongoing updates and the sharing of cutting-edge developments in MoE research, we have established a resource repository accessible at https://github.com/withinmiaov/A-Survey-on-Mixture-of-Experts.

Calibrating Bayesian Learning via Regularization, Confidence Minimization, and Selective Inference

The application of artificial intelligence (AI) models in fields such as engineering is limited by the known difficulty of quantifying the reliability of an AI's decision. A well-calibrated AI model must correctly report its accuracy on in-distribution (ID) inputs, while also enabling the detection of out-of-distribution (OOD) inputs. A conventional approach to improve calibration is the application of Bayesian ensembling. However, owing to computational limitations and model misspecification, practical ensembling strategies do not necessarily enhance calibration. This paper proposes an extension of variational inference (VI)-based Bayesian learning that integrates calibration regularization for improved ID performance, confidence minimization for OOD detection, and selective calibration to ensure a synergistic use of calibration regularization and confidence minimization. The scheme is constructed successively by first introducing calibration-regularized Bayesian learning (CBNN), then incorporating out-of-distribution confidence minimization (OCM) to yield CBNN-OCM, and finally integrating also selective calibration to produce selective CBNN-OCM (SCBNN-OCM). Selective calibration rejects inputs for which the calibration performance is expected to be insufficient. Numerical results illustrate the trade-offs between ID accuracy, ID calibration, and OOD calibration attained by both frequentist and Bayesian learning methods. Among the main conclusions, SCBNN-OCM is seen to achieve best ID and OOD performance as compared to existing state-of-the-art approaches at the cost of rejecting a sufficiently large number of inputs.

Shortcut-connected Expert Parallelism for Accelerating Mixture-of-Experts

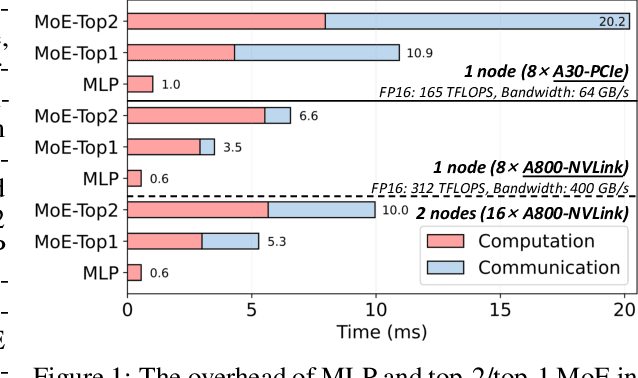
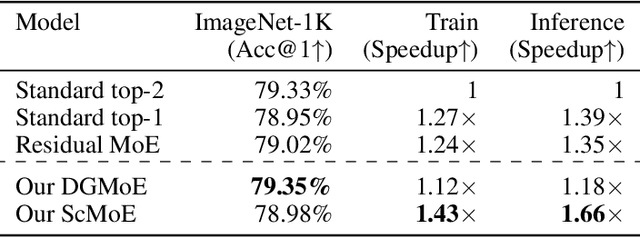
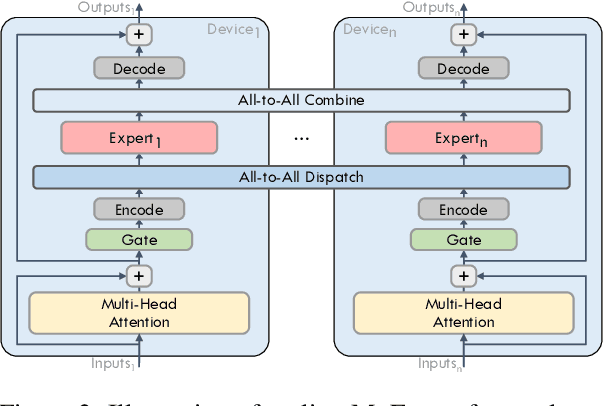
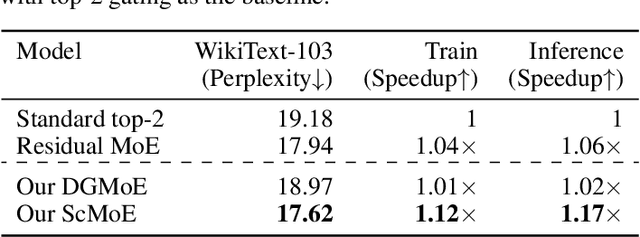
Expert parallelism has been introduced as a strategy to distribute the computational workload of sparsely-gated mixture-of-experts (MoE) models across multiple computing devices, facilitating the execution of these increasingly large-scale models. However, the All-to-All communication intrinsic to expert parallelism constitutes a significant overhead, diminishing the MoE models' efficiency. Current optimization approaches offer some relief, yet they are constrained by the sequential interdependence of communication and computation operations. To address this limitation, we present a novel shortcut-connected MoE architecture with overlapping parallel strategy, designated as ScMoE, which effectively decouples communication from its conventional sequence, allowing for a substantial overlap of 70% to 100% with computation. When compared with the prevalent top-2 MoE architecture, ScMoE demonstrates training speed improvements of 30% and 11%, and inference improvements of 40% and 15%, in our PCIe and NVLink hardware environments, respectively, where communication constitutes 60% and 15% of the total MoE time consumption. On the other hand, extensive experiments and theoretical analyses indicate that ScMoE not only achieves comparable but in some instances surpasses the model quality of existing approaches in vision and language tasks.

Horizon-Free and Instance-Dependent Regret Bounds for Reinforcement Learning with General Function Approximation

To tackle long planning horizon problems in reinforcement learning with general function approximation, we propose the first algorithm, termed as UCRL-WVTR, that achieves both \emph{horizon-free} and \emph{instance-dependent}, since it eliminates the polynomial dependency on the planning horizon. The derived regret bound is deemed \emph{sharp}, as it matches the minimax lower bound when specialized to linear mixture MDPs up to logarithmic factors. Furthermore, UCRL-WVTR is \emph{computationally efficient} with access to a regression oracle. The achievement of such a horizon-free, instance-dependent, and sharp regret bound hinges upon (i) novel algorithm designs: weighted value-targeted regression and a high-order moment estimator in the context of general function approximation; and (ii) fine-grained analyses: a novel concentration bound of weighted non-linear least squares and a refined analysis which leads to the tight instance-dependent bound. We also conduct comprehensive experiments to corroborate our theoretical findings.

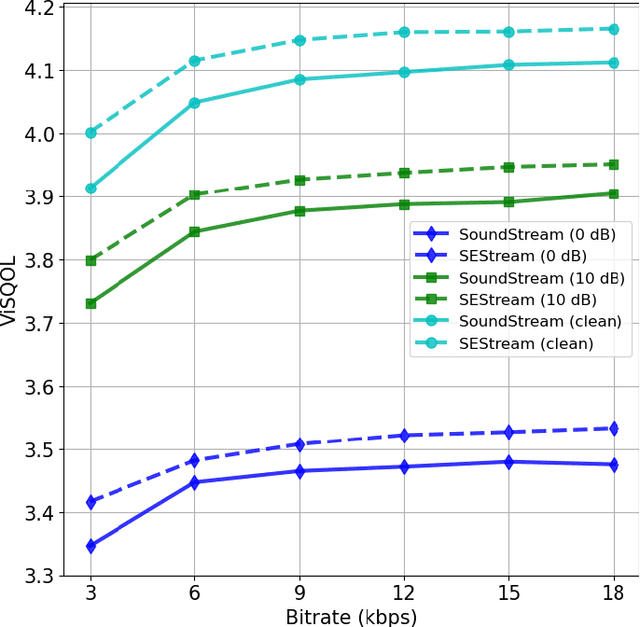
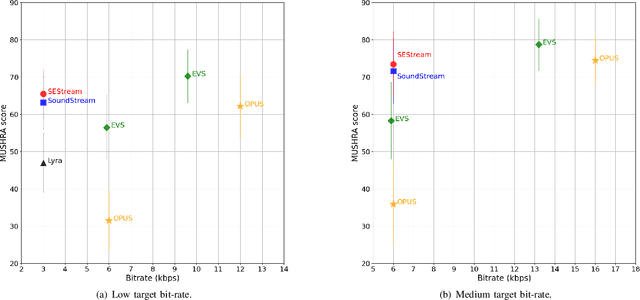
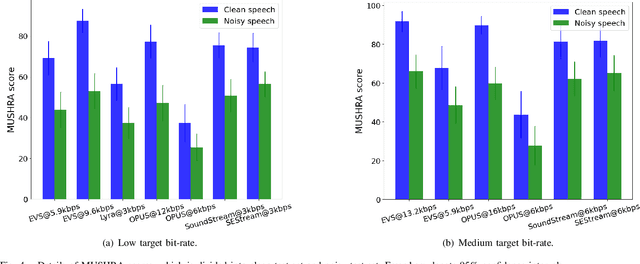
A Two-Stage Training Framework for Joint Speech Compression and Enhancement

This paper considers the joint compression and enhancement problem for speech signal in the presence of noise. Recently, the SoundStream codec, which relies on end-to-end joint training of an encoder-decoder pair and a residual vector quantizer by a combination of adversarial and reconstruction losses,has shown very promising performance, especially in subjective perception quality. In this work, we provide a theoretical result to show that, to simultaneously achieve low distortion and high perception in the presence of noise, there exist an optimal two-stage optimization procedure for the joint compression and enhancement problem. This procedure firstly optimizes an encoder-decoder pair using only distortion loss and then fixes the encoder to optimize a perceptual decoder using perception loss. Based on this result, we construct a two-stage training framework for joint compression and enhancement of noisy speech signal. Unlike existing training methods which are heuristic, the proposed two-stage training method has a theoretical foundation. Finally, experimental results for various noise and bit-rate conditions are provided. The results demonstrate that a codec trained by the proposed framework can outperform SoundStream and other representative codecs in terms of both objective and subjective evaluation metrics. Code is available at \textit{https://github.com/jscscloris/SEStream}.