Verification of Neural Networks against Convolutional Perturbations via Parameterised Kernels

We develop a method for the efficient verification of neural networks against convolutional perturbations such as blurring or sharpening. To define input perturbations we use well-known camera shake, box blur and sharpen kernels. We demonstrate that these kernels can be linearly parameterised in a way that allows for a variation of the perturbation strength while preserving desired kernel properties. To facilitate their use in neural network verification, we develop an efficient way of convolving a given input with these parameterised kernels. The result of this convolution can be used to encode the perturbation in a verification setting by prepending a linear layer to a given network. This leads to tight bounds and a high effectiveness in the resulting verification step. We add further precision by employing input splitting as a branch and bound strategy. We demonstrate that we are able to verify robustness on a number of standard benchmarks where the baseline is unable to provide any safety certificates. To the best of our knowledge, this is the first solution for verifying robustness against specific convolutional perturbations such as camera shake.

Verification of Geometric Robustness of Neural Networks via Piecewise Linear Approximation and Lipschitz Optimisation

We address the problem of verifying neural networks against geometric transformations of the input image, including rotation, scaling, shearing, and translation. The proposed method computes provably sound piecewise linear constraints for the pixel values by using sampling and linear approximations in combination with branch-and-bound Lipschitz optimisation. A feature of the method is that it obtains tighter over-approximations of the perturbation region than the present state-of-the-art. We report results from experiments on a comprehensive set of benchmarks. We show that our proposed implementation resolves more verification cases than present approaches while being more computationally efficient.

Tightening the Evaluation of PAC Bounds Using Formal Verification Results

Probably Approximately Correct (PAC) bounds are widely used to derive probabilistic guarantees for the generalisation of machine learning models. They highlight the components of the model which contribute to its generalisation capacity. However, current state-of-the-art results are loose in approximating the generalisation capacity of deployed machine learning models. Consequently, while PAC bounds are theoretically useful, their applicability for evaluating a model's generalisation property in a given operational design domain is limited. The underlying classical theory is supported by the idea that bounds can be tightened when the number of test points available to the user to evaluate the model increases. Yet, in the case of neural networks, the number of test points required to obtain bounds of interest is often impractical even for small problems. In this paper, we take the novel approach of using the formal verification of neural systems to inform the evaluation of PAC bounds. Rather than using pointwise information obtained from repeated tests, we use verification results on regions around test points. We show that conditioning existing bounds on verification results leads to a tightening proportional to the underlying probability mass of the verified region.

Tight Verification of Probabilistic Robustness in Bayesian Neural Networks

We introduce two algorithms for computing tight guarantees on the probabilistic robustness of Bayesian Neural Networks (BNNs). Computing robustness guarantees for BNNs is a significantly more challenging task than verifying the robustness of standard Neural Networks (NNs) because it requires searching the parameters' space for safe weights. Moreover, tight and complete approaches for the verification of standard NNs, such as those based on Mixed-Integer Linear Programming (MILP), cannot be directly used for the verification of BNNs because of the polynomial terms resulting from the consecutive multiplication of variables encoding the weights. Our algorithms efficiently and effectively search the parameters' space for safe weights by using iterative expansion and the network's gradient and can be used with any verification algorithm of choice for BNNs. In addition to proving that our algorithms compute tighter bounds than the SoA, we also evaluate our algorithms against the SoA on standard benchmarks, such as MNIST and CIFAR10, showing that our algorithms compute bounds up to 40% tighter than the SoA.

Expressive Losses for Verified Robustness via Convex Combinations

In order to train networks for verified adversarial robustness, previous work typically over-approximates the worst-case loss over (subsets of) perturbation regions or induces verifiability on top of adversarial training. The key to state-of-the-art performance lies in the expressivity of the employed loss function, which should be able to match the tightness of the verifiers to be employed post-training. We formalize a definition of expressivity, and show that it can be satisfied via simple convex combinations between adversarial attacks and IBP bounds. We then show that the resulting algorithms, named CC-IBP and MTL-IBP, yield state-of-the-art results across a variety of settings in spite of their conceptual simplicity. In particular, for $\ell_\infty$ perturbations of radius $\frac{1}{255}$ on TinyImageNet and downscaled ImageNet, MTL-IBP improves on the best standard and verified accuracies from the literature by from $1.98\%$ to $3.92\%$ points while only relying on single-step adversarial attacks.

Formal Verification of CNN-based Perception Systems

We address the problem of verifying neural-based perception systems implemented by convolutional neural networks. We define a notion of local robustness based on affine and photometric transformations. We show the notion cannot be captured by previously employed notions of robustness. The method proposed is based on reachability analysis for feed-forward neural networks and relies on MILP encodings of both the CNNs and transformations under question. We present an implementation and discuss the experimental results obtained for a CNN trained from the MNIST data set.

An approach to reachability analysis for feed-forward ReLU neural networks

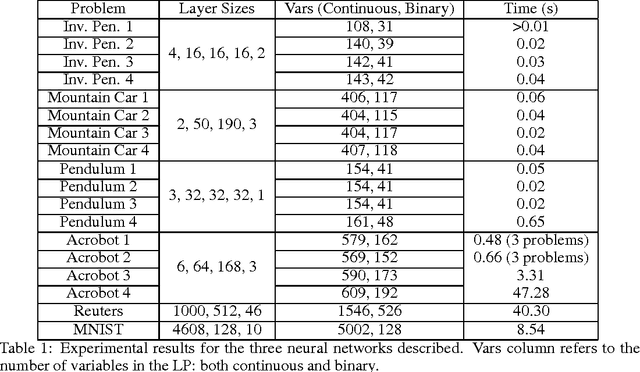
We study the reachability problem for systems implemented as feed-forward neural networks whose activation function is implemented via ReLU functions. We draw a correspondence between establishing whether some arbitrary output can ever be outputed by a neural system and linear problems characterising a neural system of interest. We present a methodology to solve cases of practical interest by means of a state-of-the-art linear programs solver. We evaluate the technique presented by discussing the experimental results obtained by analysing reachability properties for a number of benchmarks in the literature.

Interactions between Knowledge and Time in a First-Order Logic for Multi-Agent Systems: Completeness Results

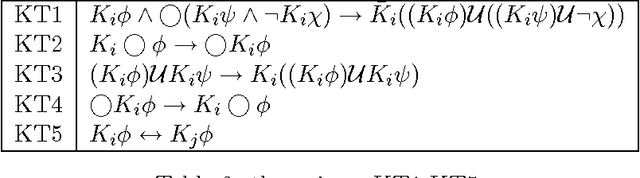
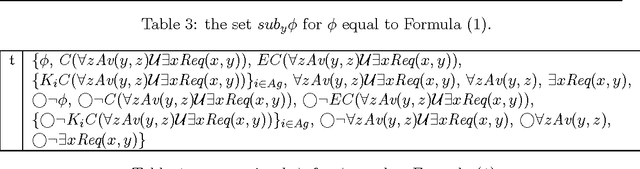
We investigate a class of first-order temporal-epistemic logics for reasoning about multi-agent systems. We encode typical properties of systems including perfect recall, synchronicity, no learning, and having a unique initial state in terms of variants of quantified interpreted systems, a first-order extension of interpreted systems. We identify several monodic fragments of first-order temporal-epistemic logic and show their completeness with respect to their corresponding classes of quantified interpreted systems.

Verification of Agent-Based Artifact Systems

Artifact systems are a novel paradigm for specifying and implementing business processes described in terms of interacting modules called artifacts. Artifacts consist of data and lifecycles, accounting respectively for the relational structure of the artifacts' states and their possible evolutions over time. In this paper we put forward artifact-centric multi-agent systems, a novel formalisation of artifact systems in the context of multi-agent systems operating on them. Differently from the usual process-based models of services, the semantics we give explicitly accounts for the data structures on which artifact systems are defined. We study the model checking problem for artifact-centric multi-agent systems against specifications written in a quantified version of temporal-epistemic logic expressing the knowledge of the agents in the exchange. We begin by noting that the problem is undecidable in general. We then identify two noteworthy restrictions, one syntactical and one semantical, that enable us to find bisimilar finite abstractions and therefore reduce the model checking problem to the instance on finite models. Under these assumptions we show that the model checking problem for these systems is EXPSPACE-complete. We then introduce artifact-centric programs, compact and declarative representations of the programs governing both the artifact system and the agents. We show that, while these in principle generate infinite-state systems, under natural conditions their verification problem can be solved on finite abstractions that can be effectively computed from the programs. Finally we exemplify the theoretical results of the paper through a mainstream procurement scenario from the artifact systems literature.