On Using Certified Training towards Empirical Robustness

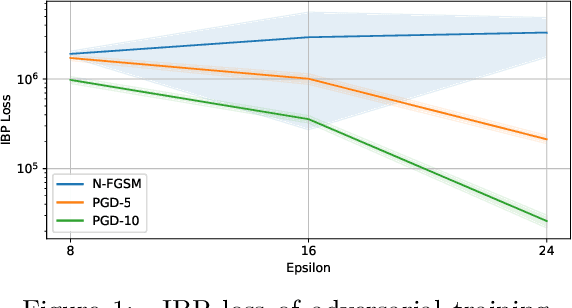
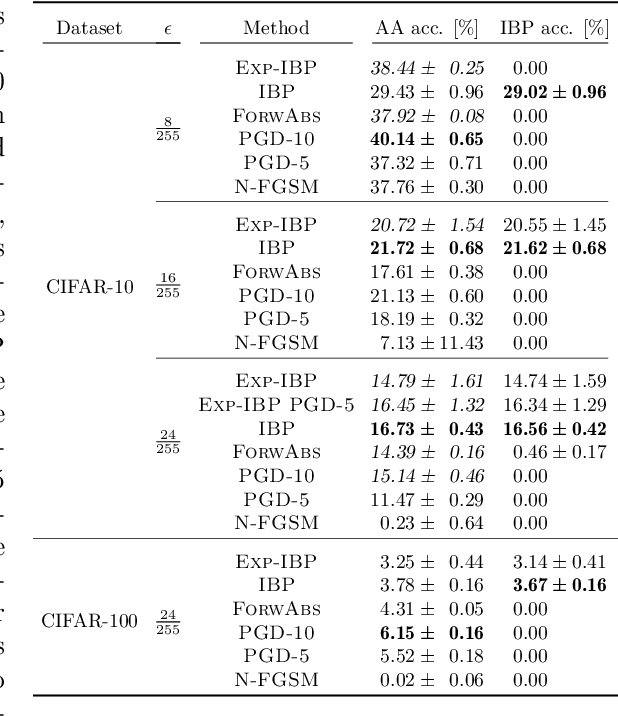
Adversarial training is arguably the most popular way to provide empirical robustness against specific adversarial examples. While variants based on multi-step attacks incur significant computational overhead, single-step variants are vulnerable to a failure mode known as catastrophic overfitting, which hinders their practical utility for large perturbations. A parallel line of work, certified training, has focused on producing networks amenable to formal guarantees of robustness against any possible attack. However, the wide gap between the best-performing empirical and certified defenses has severely limited the applicability of the latter. Inspired by recent developments in certified training, which rely on a combination of adversarial attacks with network over-approximations, and by the connections between local linearity and catastrophic overfitting, we present experimental evidence on the practical utility and limitations of using certified training towards empirical robustness. We show that, when tuned for the purpose, a recent certified training algorithm can prevent catastrophic overfitting on single-step attacks, and that it can bridge the gap to multi-step baselines under appropriate experimental settings. Finally, we present a novel regularizer for network over-approximations that can achieve similar effects while markedly reducing runtime.

Verification of Geometric Robustness of Neural Networks via Piecewise Linear Approximation and Lipschitz Optimisation

We address the problem of verifying neural networks against geometric transformations of the input image, including rotation, scaling, shearing, and translation. The proposed method computes provably sound piecewise linear constraints for the pixel values by using sampling and linear approximations in combination with branch-and-bound Lipschitz optimisation. A feature of the method is that it obtains tighter over-approximations of the perturbation region than the present state-of-the-art. We report results from experiments on a comprehensive set of benchmarks. We show that our proposed implementation resolves more verification cases than present approaches while being more computationally efficient.

Verified Neural Compressed Sensing

We develop the first (to the best of our knowledge) provably correct neural networks for a precise computational task, with the proof of correctness generated by an automated verification algorithm without any human input. Prior work on neural network verification has focused on partial specifications that, even when satisfied, are not sufficient to ensure that a neural network never makes errors. We focus on applying neural network verification to computational tasks with a precise notion of correctness, where a verifiably correct neural network provably solves the task at hand with no caveats. In particular, we develop an approach to train and verify the first provably correct neural networks for compressed sensing, i.e., recovering sparse vectors from a number of measurements smaller than the dimension of the vector. We show that for modest problem dimensions (up to 50), we can train neural networks that provably recover a sparse vector from linear and binarized linear measurements. Furthermore, we show that the complexity of the network (number of neurons/layers) can be adapted to the problem difficulty and solve problems where traditional compressed sensing methods are not known to provably work.

Expressive Losses for Verified Robustness via Convex Combinations

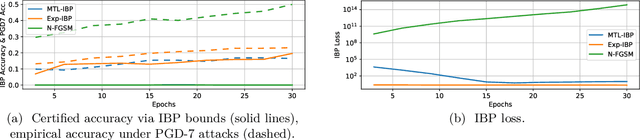
In order to train networks for verified adversarial robustness, previous work typically over-approximates the worst-case loss over (subsets of) perturbation regions or induces verifiability on top of adversarial training. The key to state-of-the-art performance lies in the expressivity of the employed loss function, which should be able to match the tightness of the verifiers to be employed post-training. We formalize a definition of expressivity, and show that it can be satisfied via simple convex combinations between adversarial attacks and IBP bounds. We then show that the resulting algorithms, named CC-IBP and MTL-IBP, yield state-of-the-art results across a variety of settings in spite of their conceptual simplicity. In particular, for $\ell_\infty$ perturbations of radius $\frac{1}{255}$ on TinyImageNet and downscaled ImageNet, MTL-IBP improves on the best standard and verified accuracies from the literature by from $1.98\%$ to $3.92\%$ points while only relying on single-step adversarial attacks.

IBP Regularization for Verified Adversarial Robustness via Branch-and-Bound

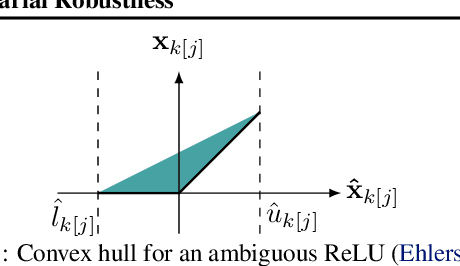
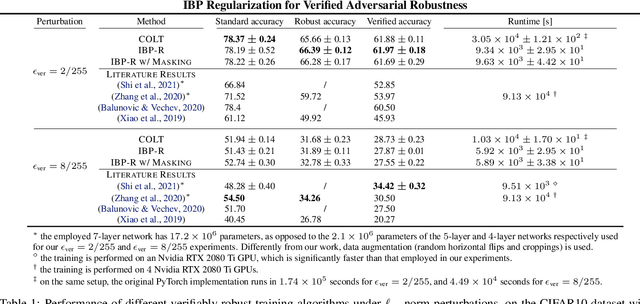
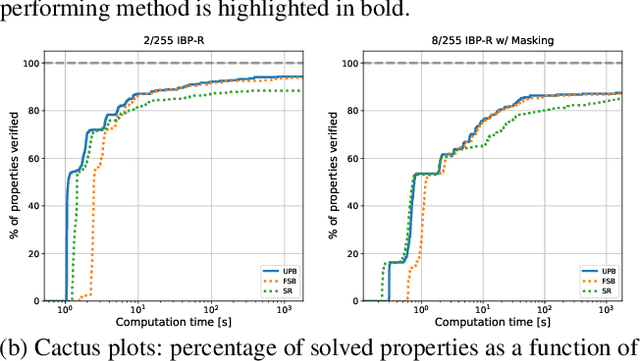
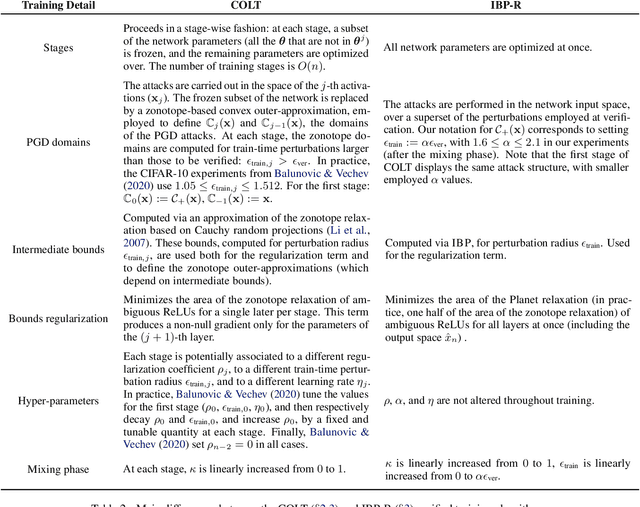
Recent works have tried to increase the verifiability of adversarially trained networks by running the attacks over domains larger than the original perturbations and adding various regularization terms to the objective. However, these algorithms either underperform or require complex and expensive stage-wise training procedures, hindering their practical applicability. We present IBP-R, a novel verified training algorithm that is both simple and effective. IBP-R induces network verifiability by coupling adversarial attacks on enlarged domains with a regularization term, based on inexpensive interval bound propagation, that minimizes the gap between the non-convex verification problem and its approximations. By leveraging recent branch-and-bound frameworks, we show that IBP-R obtains state-of-the-art verified robustness-accuracy trade-offs for small perturbations on CIFAR-10 while training significantly faster than relevant previous work. Additionally, we present UPB, a novel branching strategy that, relying on a simple heuristic based on $\beta$-CROWN, reduces the cost of state-of-the-art branching algorithms while yielding splits of comparable quality.

In Defense of the Unitary Scalarization for Deep Multi-Task Learning

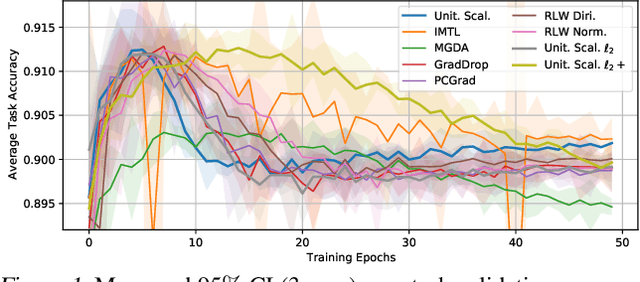
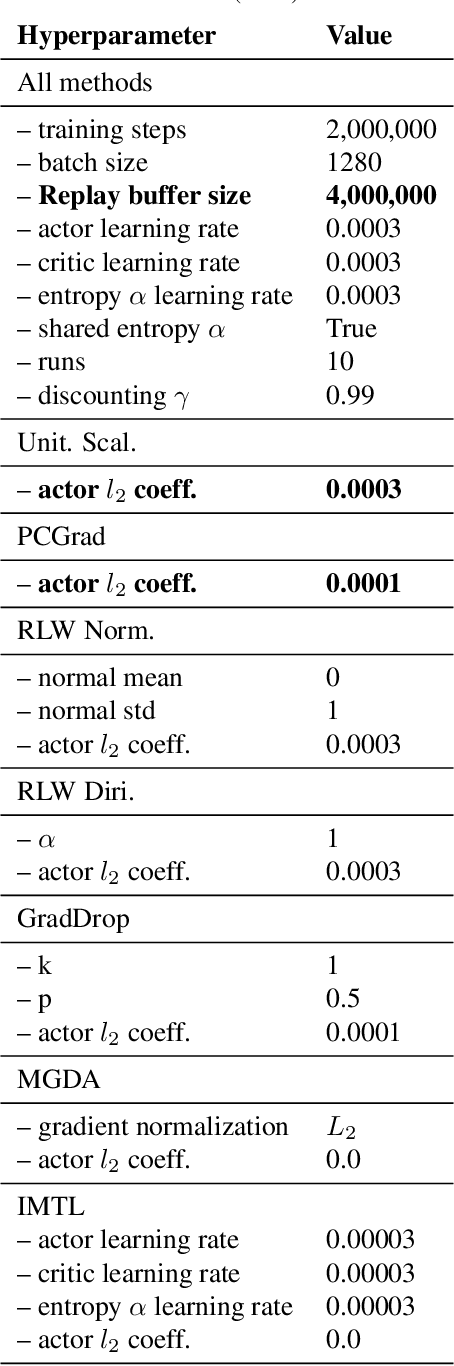
Recent multi-task learning research argues against unitary scalarization, where training simply minimizes the sum of the task losses. Several ad-hoc multi-task optimization algorithms have instead been proposed, inspired by various hypotheses about what makes multi-task settings difficult. The majority of these optimizers require per-task gradients, and introduce significant memory, runtime, and implementation overhead. We present a theoretical analysis suggesting that many specialized multi-task optimizers can be interpreted as forms of regularization. Moreover, we show that, when coupled with standard regularization and stabilization techniques from single-task learning, unitary scalarization matches or improves upon the performance of complex multi-task optimizers in both supervised and reinforcement learning settings. We believe our results call for a critical reevaluation of recent research in the area.

Improved Branch and Bound for Neural Network Verification via Lagrangian Decomposition

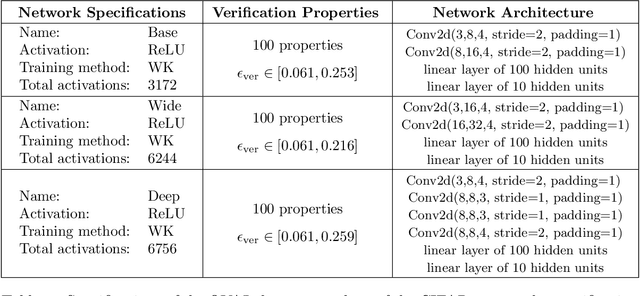
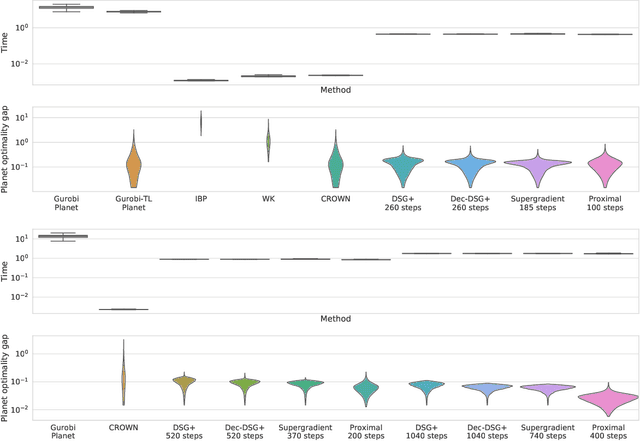
We improve the scalability of Branch and Bound (BaB) algorithms for formally proving input-output properties of neural networks. First, we propose novel bounding algorithms based on Lagrangian Decomposition. Previous works have used off-the-shelf solvers to solve relaxations at each node of the BaB tree, or constructed weaker relaxations that can be solved efficiently, but lead to unnecessarily weak bounds. Our formulation restricts the optimization to a subspace of the dual domain that is guaranteed to contain the optimum, resulting in accelerated convergence. Furthermore, it allows for a massively parallel implementation, which is amenable to GPU acceleration via modern deep learning frameworks. Second, we present a novel activation-based branching strategy. By coupling an inexpensive heuristic with fast dual bounding, our branching scheme greatly reduces the size of the BaB tree compared to previous heuristic methods. Moreover, it performs competitively with a recent strategy based on learning algorithms, without its large offline training cost. Finally, we design a BaB framework, named Branch and Dual Network Bound (BaDNB), based on our novel bounding and branching algorithms. We show that BaDNB outperforms previous complete verification systems by a large margin, cutting average verification times by factors up to 50 on adversarial robustness properties.

Scaling the Convex Barrier with Sparse Dual Algorithms

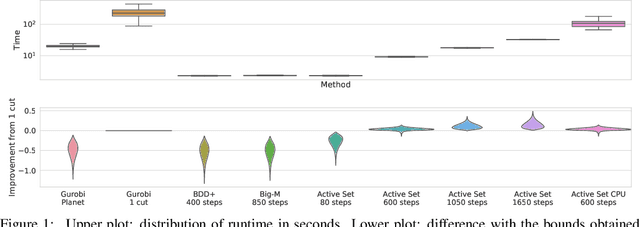
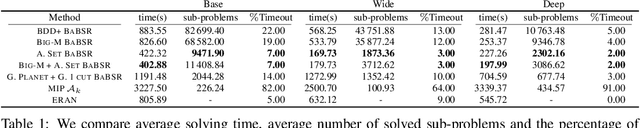
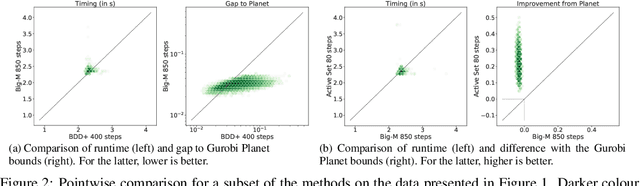
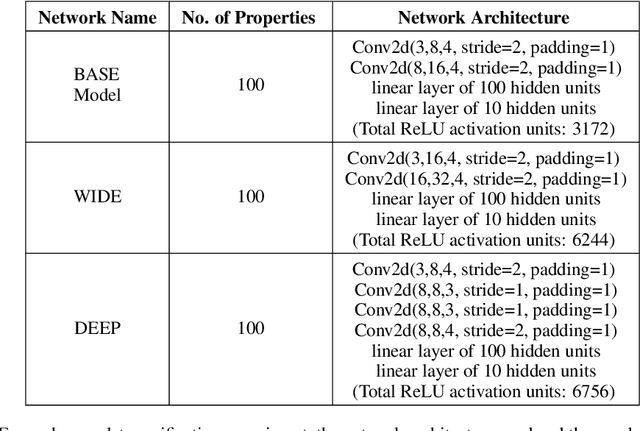
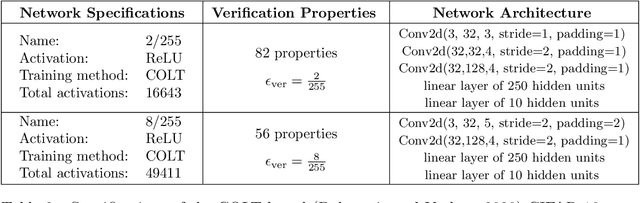
Tight and efficient neural network bounding is crucial to the scaling of neural network verification systems. Many efficient bounding algorithms have been presented recently, but they are often too loose to verify more challenging properties. This is due to the weakness of the employed relaxation, which is usually a linear program of size linear in the number of neurons. While a tighter linear relaxation for piecewise-linear activations exists, it comes at the cost of exponentially many constraints and currently lacks an efficient customized solver. We alleviate this deficiency by presenting two novel dual algorithms: one operates a subgradient method on a small active set of dual variables, the other exploits the sparsity of Frank-Wolfe type optimizers to incur only a linear memory cost. Both methods recover the strengths of the new relaxation: tightness and a linear separation oracle. At the same time, they share the benefits of previous dual approaches for weaker relaxations: massive parallelism, GPU implementation, low cost per iteration and valid bounds at any time. As a consequence, we can obtain better bounds than off-the-shelf solvers in only a fraction of their running time, attaining significant formal verification speed-ups.

Lagrangian Decomposition for Neural Network Verification

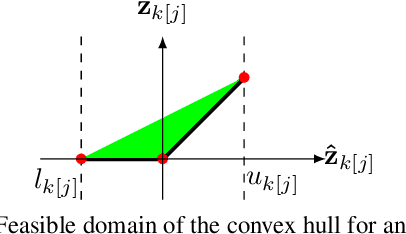
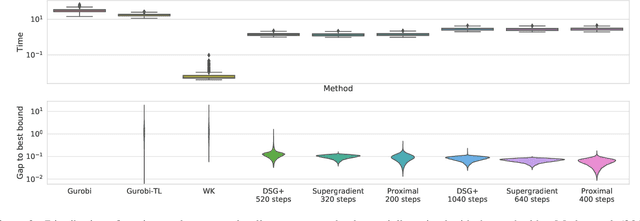
A fundamental component of neural network verification is the computation of bounds on the values their outputs can take. Previous methods have either used off-the-shelf solvers, discarding the problem structure, or relaxed the problem even further, making the bounds unnecessarily loose. We propose a novel approach based on Lagrangian Decomposition. Our formulation admits an efficient supergradient ascent algorithm, as well as an improved proximal algorithm. Both the algorithms offer three advantages: (i) they yield bounds that are provably at least as tight as previous dual algorithms relying on Lagrangian relaxations; (ii) they are based on operations analogous to forward/backward pass of neural networks layers and are therefore easily parallelizable, amenable to GPU implementation and able to take advantage of the convolutional structure of problems; and (iii) they allow for anytime stopping while still providing valid bounds. Empirically, we show that we obtain bounds comparable with off-the-shelf solvers in a fraction of their running time, and obtain tighter bounds in the same time as previous dual algorithms. This results in an overall speed-up when employing the bounds for formal verification.

Sampling Acquisition Functions for Batch Bayesian Optimization

This paper presents Acquisition Thompson Sampling (ATS), a novel algorithm for batch Bayesian Optimization (BO) based on the idea of sampling multiple acquisition functions from a stochastic process. We define this process through the dependency of the acquisition functions on a set of model parameters. ATS is conceptually simple, straightforward to implement and, unlike other batch BO methods, it can be employed to parallelize any sequential acquisition function. In order to improve performance for multi-modal tasks, we show that ATS can be combined with existing techniques in order to realize different explore-exploit trade-offs and take into account pending function evaluations. We present experiments on a variety of benchmark functions and on the hyper-parameter optimization of a popular gradient boosting tree algorithm. These demonstrate the competitiveness of our algorithm with two state-of-the-art batch BO methods, and its advantages to classical parallel Thompson Sampling for BO.