On Using Certified Training towards Empirical Robustness

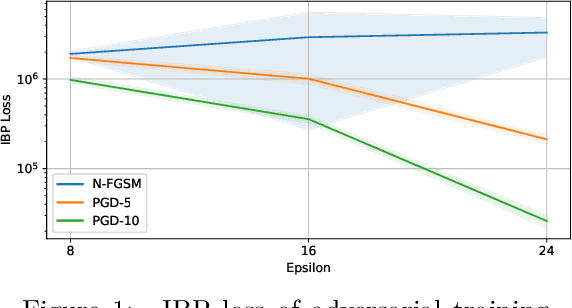
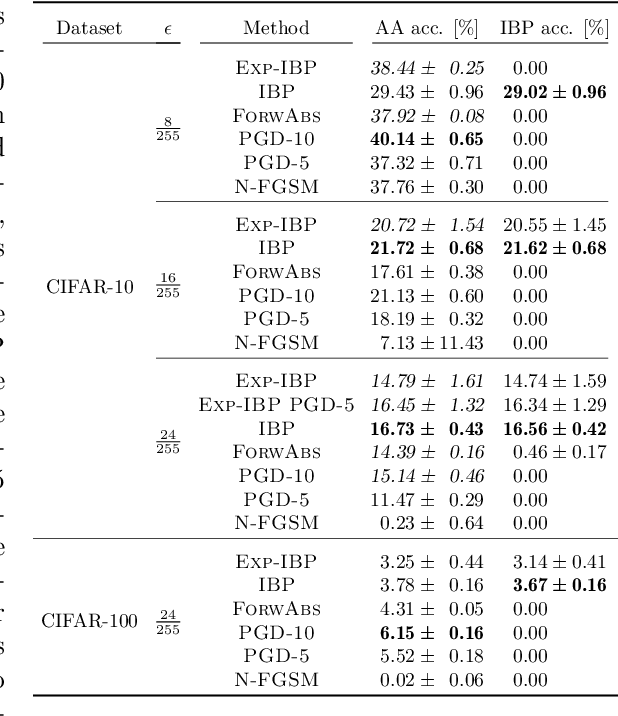
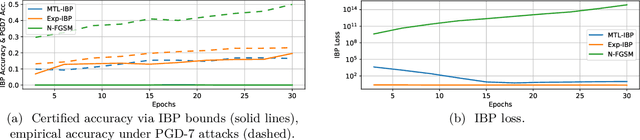
Adversarial training is arguably the most popular way to provide empirical robustness against specific adversarial examples. While variants based on multi-step attacks incur significant computational overhead, single-step variants are vulnerable to a failure mode known as catastrophic overfitting, which hinders their practical utility for large perturbations. A parallel line of work, certified training, has focused on producing networks amenable to formal guarantees of robustness against any possible attack. However, the wide gap between the best-performing empirical and certified defenses has severely limited the applicability of the latter. Inspired by recent developments in certified training, which rely on a combination of adversarial attacks with network over-approximations, and by the connections between local linearity and catastrophic overfitting, we present experimental evidence on the practical utility and limitations of using certified training towards empirical robustness. We show that, when tuned for the purpose, a recent certified training algorithm can prevent catastrophic overfitting on single-step attacks, and that it can bridge the gap to multi-step baselines under appropriate experimental settings. Finally, we present a novel regularizer for network over-approximations that can achieve similar effects while markedly reducing runtime.

Towards Dependable Autonomous Systems Based on Bayesian Deep Learning Components

As autonomous systems increasingly rely on Deep Neural Networks (DNN) to implement the navigation pipeline functions, uncertainty estimation methods have become paramount for estimating confidence in DNN predictions. Bayesian Deep Learning (BDL) offers a principled approach to model uncertainties in DNNs. However, in DNN-based systems, not all the components use uncertainty estimation methods and typically ignore the uncertainty propagation between them. This paper provides a method that considers the uncertainty and the interaction between BDL components to capture the overall system uncertainty. We study the effect of uncertainty propagation in a BDL-based system for autonomous aerial navigation. Experiments show that our approach allows us to capture useful uncertainty estimates while slightly improving the system's performance in its final task. In addition, we discuss the benefits, challenges, and implications of adopting BDL to build dependable autonomous systems.

Improving Robustness of Deep Neural Networks for Aerial Navigation by Incorporating Input Uncertainty

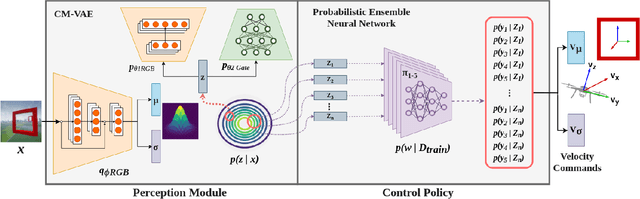
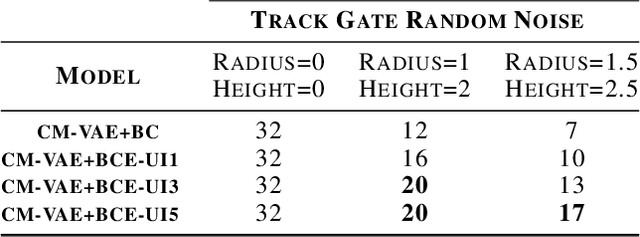
Uncertainty quantification methods are required in autonomous systems that include deep learning (DL) components to assess the confidence of their estimations. However, to successfully deploy DL components in safety-critical autonomous systems, they should also handle uncertainty at the input rather than only at the output of the DL components. Considering a probability distribution in the input enables the propagation of uncertainty through different components to provide a representative measure of the overall system uncertainty. In this position paper, we propose a method to account for uncertainty at the input of Bayesian Deep Learning control policies for Aerial Navigation. Our early experiments show that the proposed method improves the robustness of the navigation policy in Out-of-Distribution (OoD) scenarios.

A Comparison of Uncertainty Estimation Approaches in Deep Learning Components for Autonomous Vehicle Applications

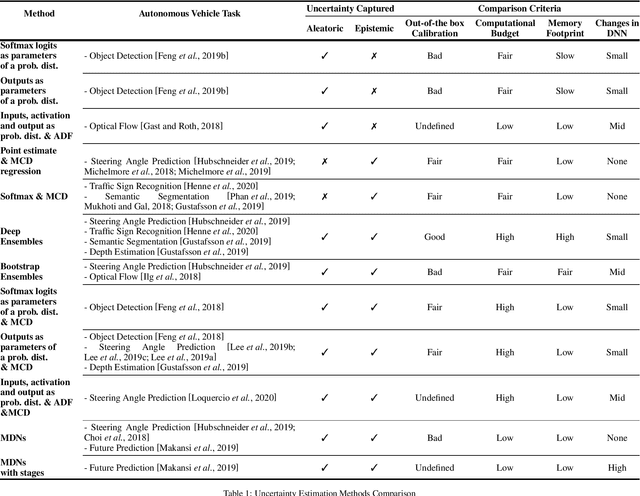
A key factor for ensuring safety in Autonomous Vehicles (AVs) is to avoid any abnormal behaviors under undesirable and unpredicted circumstances. As AVs increasingly rely on Deep Neural Networks (DNNs) to perform safety-critical tasks, different methods for uncertainty quantification have recently been proposed to measure the inevitable source of errors in data and models. However, uncertainty quantification in DNNs is still a challenging task. These methods require a higher computational load, a higher memory footprint, and introduce extra latency, which can be prohibitive in safety-critical applications. In this paper, we provide a brief and comparative survey of methods for uncertainty quantification in DNNs along with existing metrics to evaluate uncertainty predictions. We are particularly interested in understanding the advantages and downsides of each method for specific AV tasks and types of uncertainty sources.