Search-based Methods for Multi-Cloud Configuration

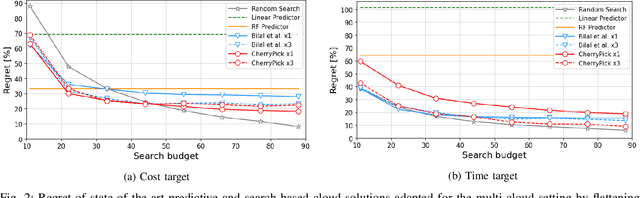
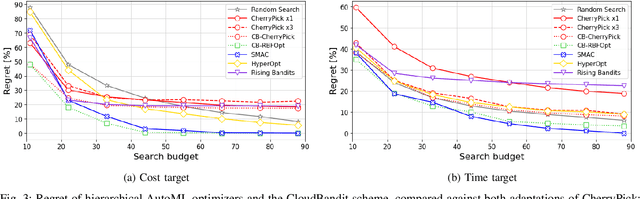
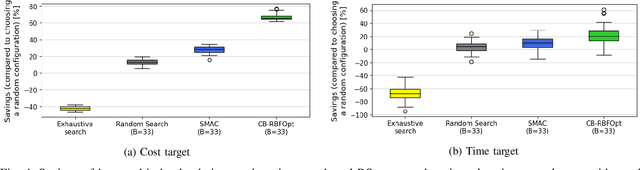
Multi-cloud computing has become increasingly popular with enterprises looking to avoid vendor lock-in. While most cloud providers offer similar functionality, they may differ significantly in terms of performance and/or cost. A customer looking to benefit from such differences will naturally want to solve the multi-cloud configuration problem: given a workload, which cloud provider should be chosen and how should its nodes be configured in order to minimize runtime or cost? In this work, we consider solutions to this optimization problem. We develop and evaluate possible adaptations of state-of-the-art cloud configuration solutions to the multi-cloud domain. Furthermore, we identify an analogy between multi-cloud configuration and the selection-configuration problems commonly studied in the automated machine learning (AutoML) field. Inspired by this connection, we utilize popular optimizers from AutoML to solve multi-cloud configuration. Finally, we propose a new algorithm for solving multi-cloud configuration, CloudBandit (CB). It treats the outer problem of cloud provider selection as a best-arm identification problem, in which each arm pull corresponds to running an arbitrary black-box optimizer on the inner problem of node configuration. Our experiments indicate that (a) many state-of-the-art cloud configuration solutions can be adapted to multi-cloud, with best results obtained for adaptations which utilize the hierarchical structure of the multi-cloud configuration domain, (b) hierarchical methods from AutoML can be used for the multi-cloud configuration task and can outperform state-of-the-art cloud configuration solutions and (c) CB achieves competitive or lower regret relative to other tested algorithms, whilst also identifying configurations that have 65% lower median cost and 20% lower median time in production, compared to choosing a random provider and configuration.

MixBoost: A Heterogeneous Boosting Machine

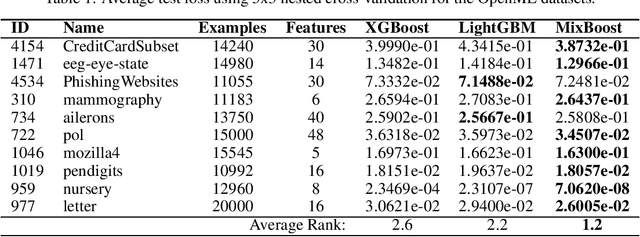
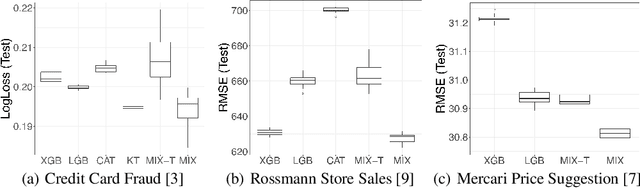
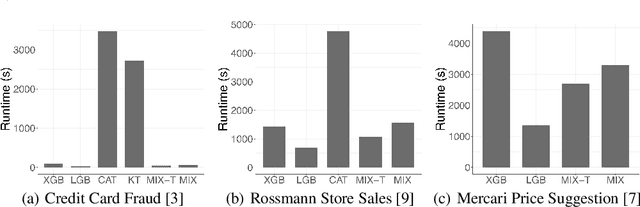
Modern gradient boosting software frameworks, such as XGBoost and LightGBM, implement Newton descent in a functional space. At each boosting iteration, their goal is to find the base hypothesis, selected from some base hypothesis class, that is closest to the Newton descent direction in a Euclidean sense. Typically, the base hypothesis class is fixed to be all binary decision trees up to a given depth. In this work, we study a Heterogeneous Newton Boosting Machine (HNBM) in which the base hypothesis class may vary across boosting iterations. Specifically, at each boosting iteration, the base hypothesis class is chosen, from a fixed set of subclasses, by sampling from a probability distribution. We derive a global linear convergence rate for the HNBM under certain assumptions, and show that it agrees with existing rates for Newton's method when the Newton direction can be perfectly fitted by the base hypothesis at each boosting iteration. We then describe a particular realization of a HNBM, MixBoost, that, at each boosting iteration, randomly selects between either a decision tree of variable depth or a linear regressor with random Fourier features. We describe how MixBoost is implemented, with a focus on the training complexity. Finally, we present experimental results, using OpenML and Kaggle datasets, that show that MixBoost is able to achieve better generalization loss than competing boosting frameworks, without taking significantly longer to tune.

Sampling Acquisition Functions for Batch Bayesian Optimization

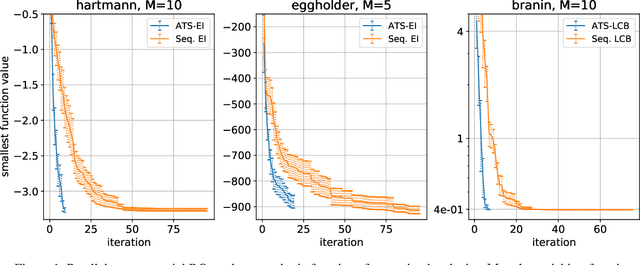
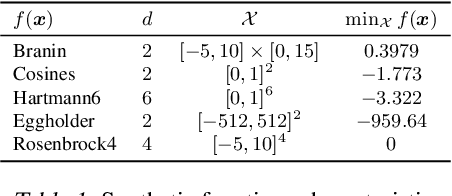
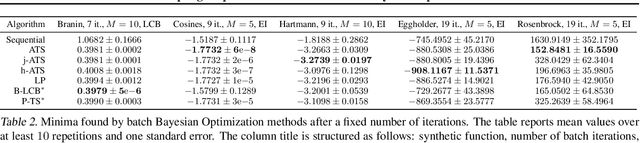
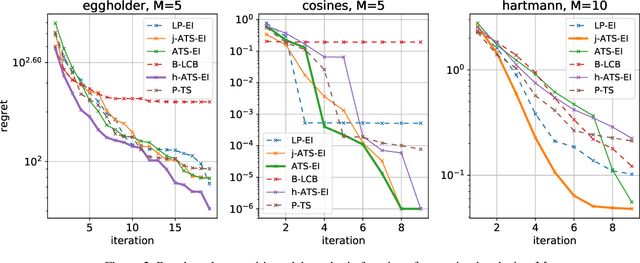
This paper presents Acquisition Thompson Sampling (ATS), a novel algorithm for batch Bayesian Optimization (BO) based on the idea of sampling multiple acquisition functions from a stochastic process. We define this process through the dependency of the acquisition functions on a set of model parameters. ATS is conceptually simple, straightforward to implement and, unlike other batch BO methods, it can be employed to parallelize any sequential acquisition function. In order to improve performance for multi-modal tasks, we show that ATS can be combined with existing techniques in order to realize different explore-exploit trade-offs and take into account pending function evaluations. We present experiments on a variety of benchmark functions and on the hyper-parameter optimization of a popular gradient boosting tree algorithm. These demonstrate the competitiveness of our algorithm with two state-of-the-art batch BO methods, and its advantages to classical parallel Thompson Sampling for BO.

Benchmarking and Optimization of Gradient Boosting Decision Tree Algorithms

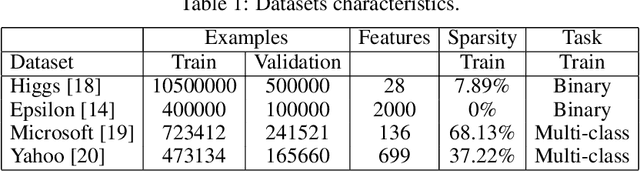
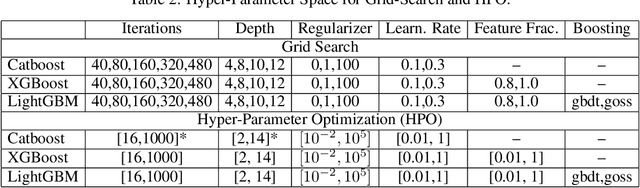
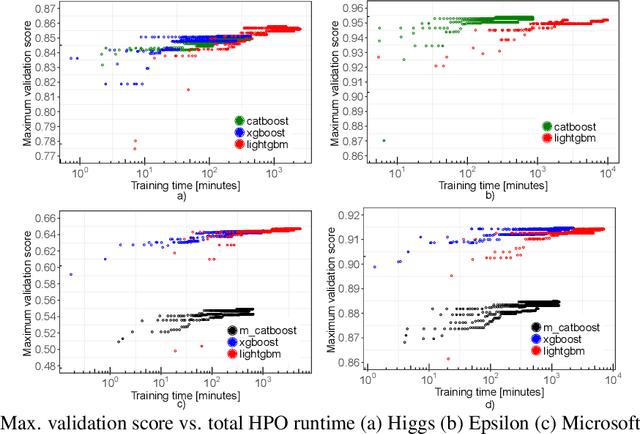
Gradient boosting decision trees (GBDTs) have seen widespread adoption in academia, industry and competitive data science due to their state-of-the-art performance in many machine learning tasks. One relative downside to these models is the large number of hyper-parameters that they expose to the end-user. To maximize the predictive power of GBDT models, one must either manually tune the hyper-parameters, or utilize automated techniques such as those based on Bayesian optimization. Both of these approaches are time-consuming since they involve repeatably training the model for different sets of hyper-parameters. A number of software GBDT packages have started to offer GPU acceleration which can help to alleviate this problem. In this paper, we consider three such packages: XGBoost, LightGBM and Catboost. Firstly, we evaluate the performance of the GPU acceleration provided by these packages using large-scale datasets with varying shapes, sparsities and learning tasks. Then, we compare the packages in the context of hyper-parameter optimization, both in terms of how quickly each package converges to a good validation score, and in terms of generalization performance.

Snap ML: A Hierarchical Framework for Machine Learning

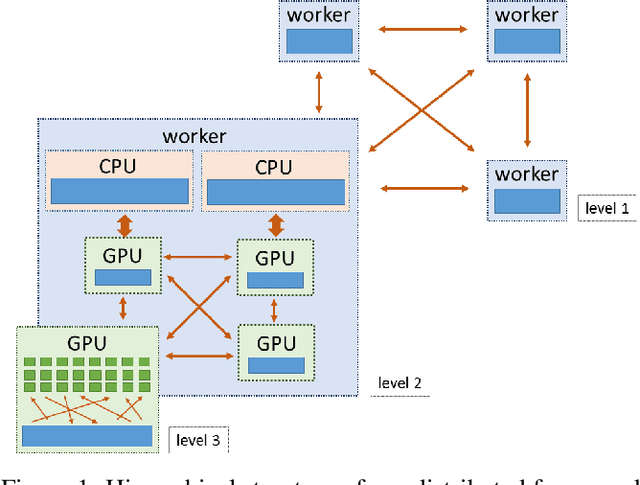
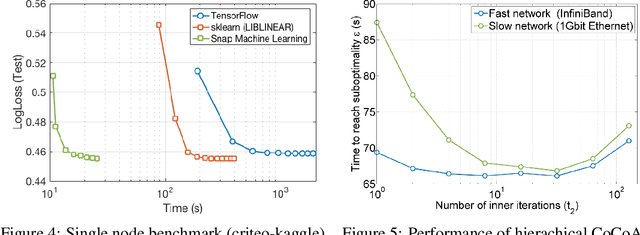
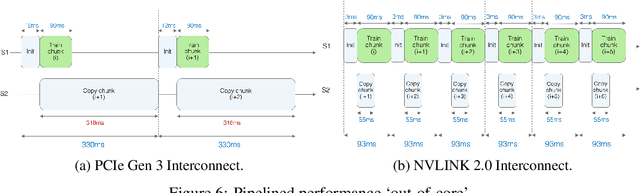
We describe a new software framework for fast training of generalized linear models. The framework, named Snap Machine Learning (Snap ML), combines recent advances in machine learning systems and algorithms in a nested manner to reflect the hierarchical architecture of modern computing systems. We prove theoretically that such a hierarchical system can accelerate training in distributed environments where intra-node communication is cheaper than inter-node communication. Additionally, we provide a review of the implementation of Snap ML in terms of GPU acceleration, pipelining, communication patterns and software architecture, highlighting aspects that were critical for achieving high performance. We evaluate the performance of Snap ML in both single-node and multi-node environments, quantifying the benefit of the hierarchical scheme and the data streaming functionality, and comparing with other widely-used machine learning software frameworks. Finally, we present a logistic regression benchmark on the Criteo Terabyte Click Logs dataset and show that Snap ML achieves the same test loss an order of magnitude faster than any of the previously reported results.

Understanding and Optimizing the Performance of Distributed Machine Learning Applications on Apache Spark

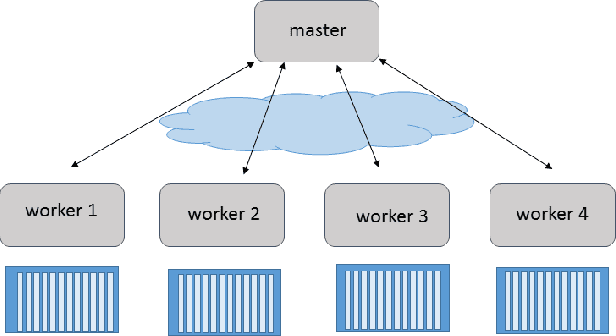
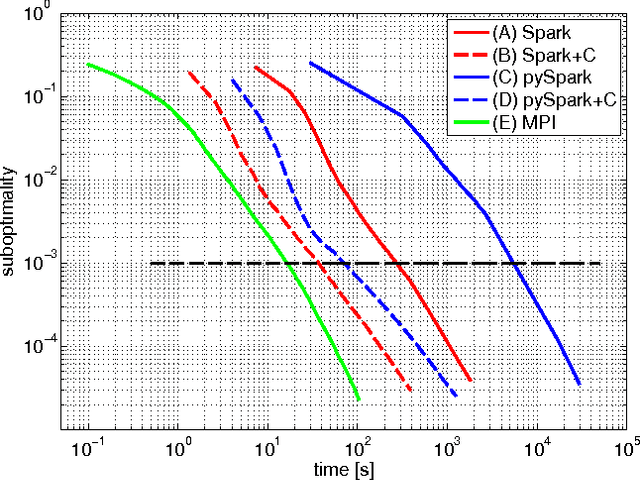
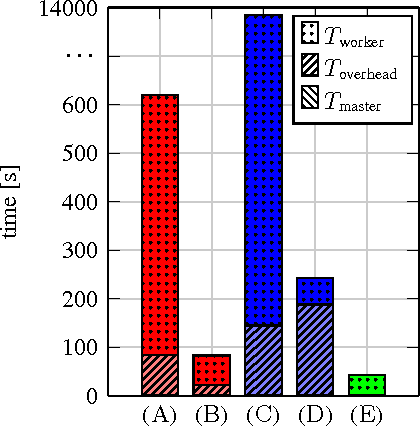
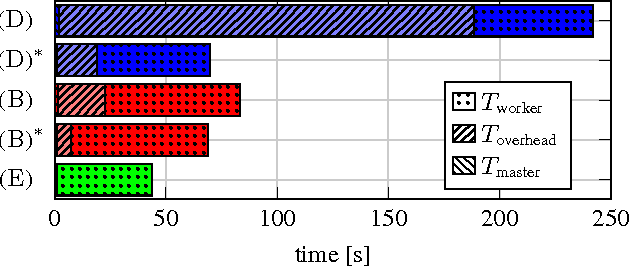
In this paper we explore the performance limits of Apache Spark for machine learning applications. We begin by analyzing the characteristics of a state-of-the-art distributed machine learning algorithm implemented in Spark and compare it to an equivalent reference implementation using the high performance computing framework MPI. We identify critical bottlenecks of the Spark framework and carefully study their implications on the performance of the algorithm. In order to improve Spark performance we then propose a number of practical techniques to alleviate some of its overheads. However, optimizing computational efficiency and framework related overheads is not the only key to performance -- we demonstrate that in order to get the best performance out of any implementation it is necessary to carefully tune the algorithm to the respective trade-off between computation time and communication latency. The optimal trade-off depends on both the properties of the distributed algorithm as well as infrastructure and framework-related characteristics. Finally, we apply these technical and algorithmic optimizations to three different distributed linear machine learning algorithms that have been implemented in Spark. We present results using five large datasets and demonstrate that by using the proposed optimizations, we can achieve a reduction in the performance difference between Spark and MPI from 20x to 2x.