Malgorzata Lazuka
MixBoost: A Heterogeneous Boosting Machine
Jun 17, 2020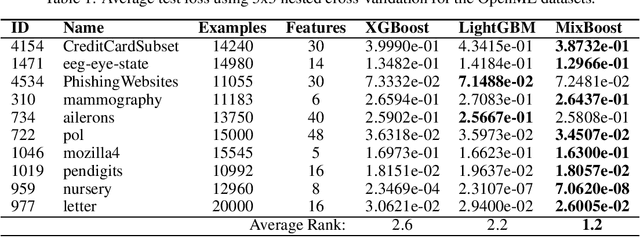
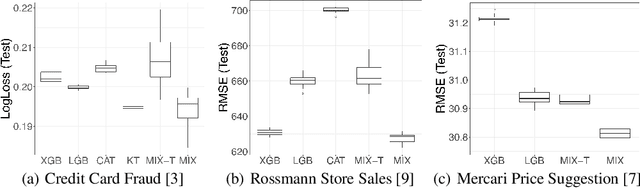
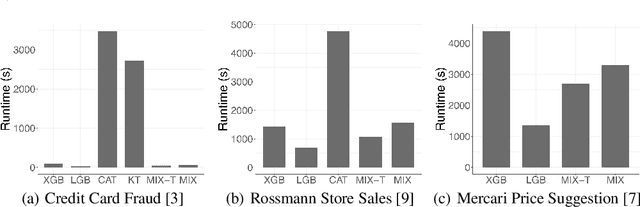

Abstract:Modern gradient boosting software frameworks, such as XGBoost and LightGBM, implement Newton descent in a functional space. At each boosting iteration, their goal is to find the base hypothesis, selected from some base hypothesis class, that is closest to the Newton descent direction in a Euclidean sense. Typically, the base hypothesis class is fixed to be all binary decision trees up to a given depth. In this work, we study a Heterogeneous Newton Boosting Machine (HNBM) in which the base hypothesis class may vary across boosting iterations. Specifically, at each boosting iteration, the base hypothesis class is chosen, from a fixed set of subclasses, by sampling from a probability distribution. We derive a global linear convergence rate for the HNBM under certain assumptions, and show that it agrees with existing rates for Newton's method when the Newton direction can be perfectly fitted by the base hypothesis at each boosting iteration. We then describe a particular realization of a HNBM, MixBoost, that, at each boosting iteration, randomly selects between either a decision tree of variable depth or a linear regressor with random Fourier features. We describe how MixBoost is implemented, with a focus on the training complexity. Finally, we present experimental results, using OpenML and Kaggle datasets, that show that MixBoost is able to achieve better generalization loss than competing boosting frameworks, without taking significantly longer to tune.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge