Celestine Dünner
Parallel training of linear models without compromising convergence
Nov 05, 2018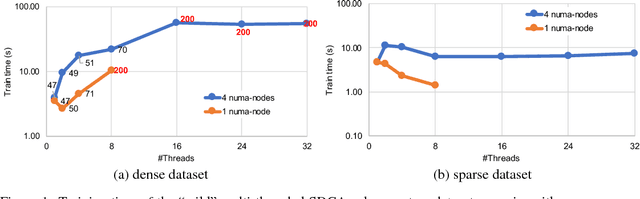
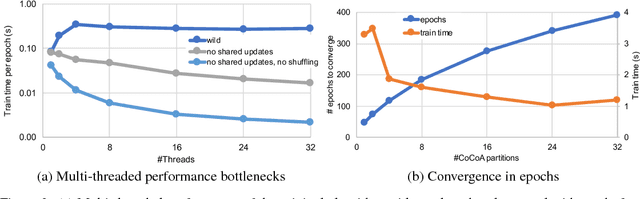
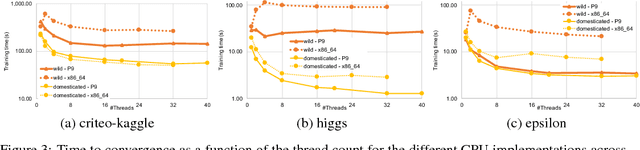
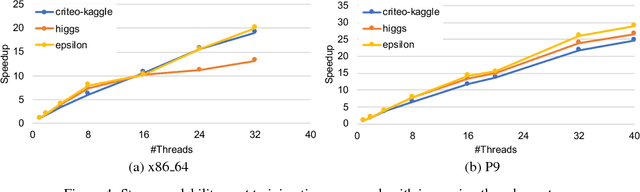
Abstract:In this paper we analyze, evaluate, and improve the performance of training generalized linear models on modern CPUs. We start with a state-of-the-art asynchronous parallel training algorithm, identify system-level performance bottlenecks, and apply optimizations that improve data parallelism, cache line locality, and cache line prefetching of the algorithm. These modifications reduce the per-epoch run-time significantly, but take a toll on algorithm convergence in terms of the required number of epochs. To alleviate these shortcomings of our systems-optimized version, we propose a novel, dynamic data partitioning scheme across threads which allows us to approach the convergence of the sequential version. The combined set of optimizations result in a consistent bottom line speedup in convergence of up to $\times12$ compared to the initial asynchronous parallel training algorithm and up to $\times42$, compared to state of the art implementations (scikit-learn and h2o) on a range of multi-core CPU architectures.
A Distributed Second-Order Algorithm You Can Trust
Jun 20, 2018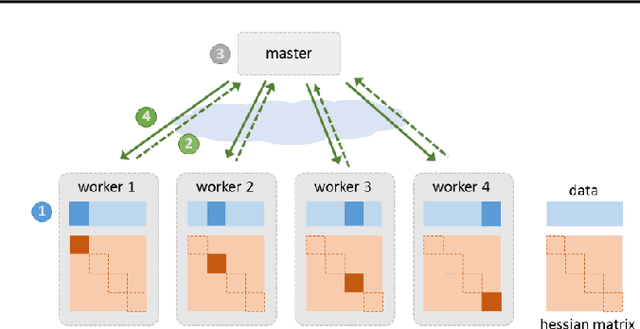
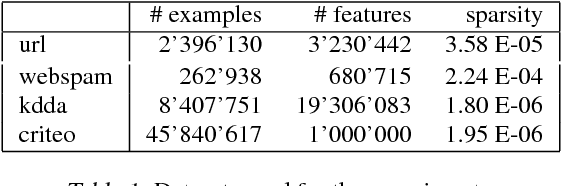
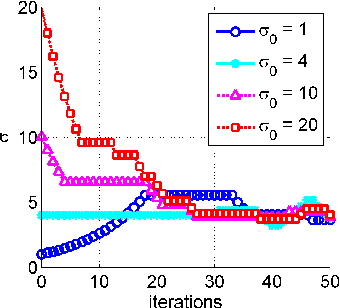
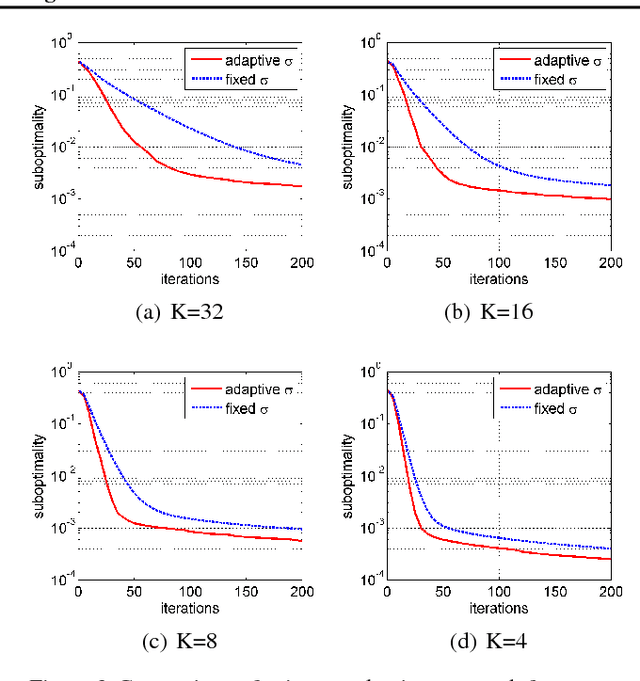
Abstract:Due to the rapid growth of data and computational resources, distributed optimization has become an active research area in recent years. While first-order methods seem to dominate the field, second-order methods are nevertheless attractive as they potentially require fewer communication rounds to converge. However, there are significant drawbacks that impede their wide adoption, such as the computation and the communication of a large Hessian matrix. In this paper we present a new algorithm for distributed training of generalized linear models that only requires the computation of diagonal blocks of the Hessian matrix on the individual workers. To deal with this approximate information we propose an adaptive approach that - akin to trust-region methods - dynamically adapts the auxiliary model to compensate for modeling errors. We provide theoretical rates of convergence for a wide class of problems including L1-regularized objectives. We also demonstrate that our approach achieves state-of-the-art results on multiple large benchmark datasets.
Snap ML: A Hierarchical Framework for Machine Learning
Jun 18, 2018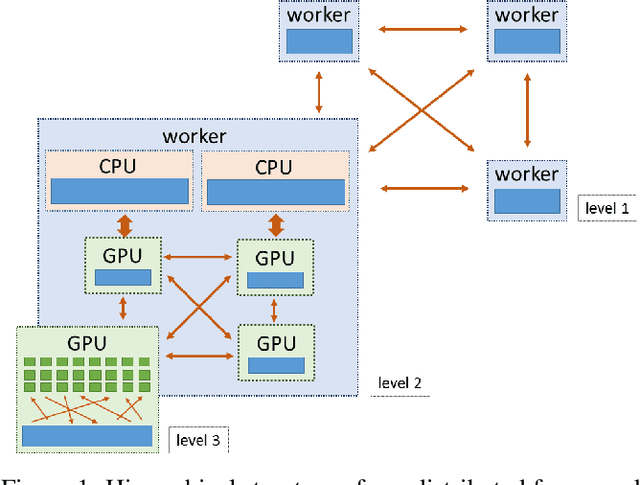

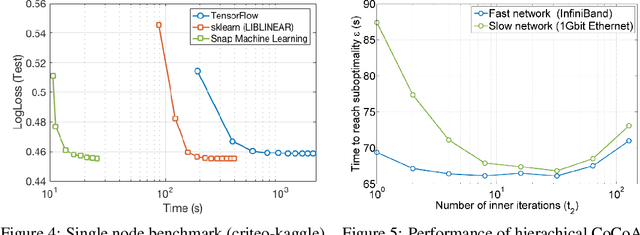
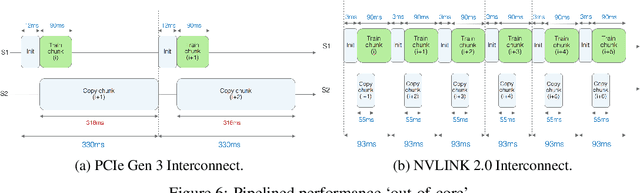
Abstract:We describe a new software framework for fast training of generalized linear models. The framework, named Snap Machine Learning (Snap ML), combines recent advances in machine learning systems and algorithms in a nested manner to reflect the hierarchical architecture of modern computing systems. We prove theoretically that such a hierarchical system can accelerate training in distributed environments where intra-node communication is cheaper than inter-node communication. Additionally, we provide a review of the implementation of Snap ML in terms of GPU acceleration, pipelining, communication patterns and software architecture, highlighting aspects that were critical for achieving high performance. We evaluate the performance of Snap ML in both single-node and multi-node environments, quantifying the benefit of the hierarchical scheme and the data streaming functionality, and comparing with other widely-used machine learning software frameworks. Finally, we present a logistic regression benchmark on the Criteo Terabyte Click Logs dataset and show that Snap ML achieves the same test loss an order of magnitude faster than any of the previously reported results.
Understanding and Optimizing the Performance of Distributed Machine Learning Applications on Apache Spark
Dec 13, 2017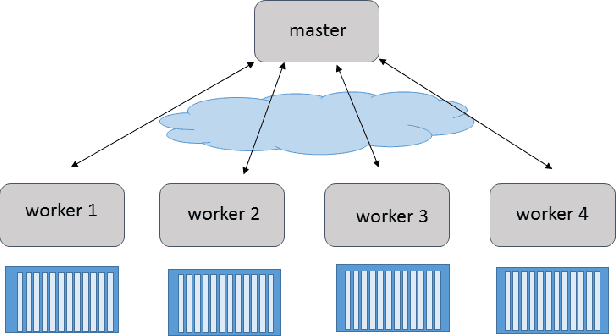
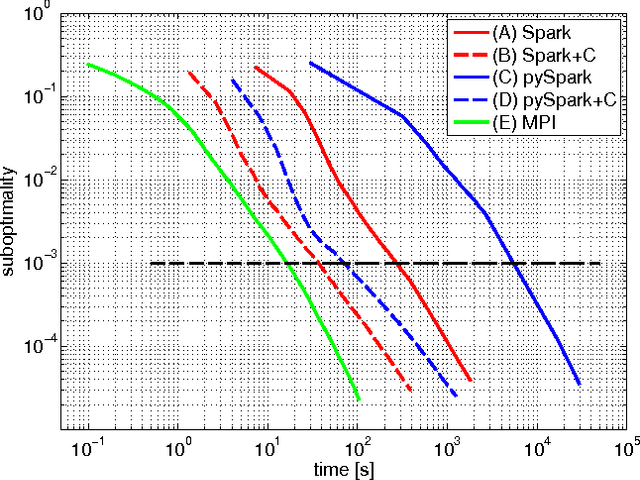
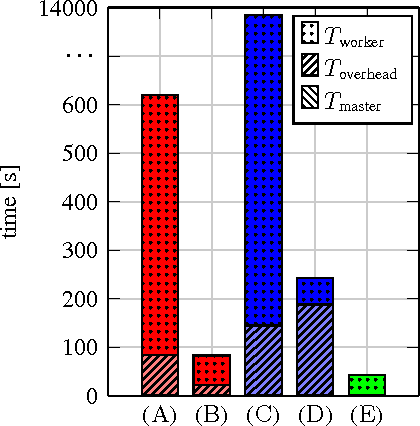
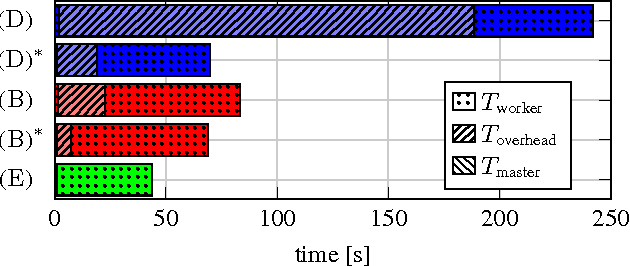
Abstract:In this paper we explore the performance limits of Apache Spark for machine learning applications. We begin by analyzing the characteristics of a state-of-the-art distributed machine learning algorithm implemented in Spark and compare it to an equivalent reference implementation using the high performance computing framework MPI. We identify critical bottlenecks of the Spark framework and carefully study their implications on the performance of the algorithm. In order to improve Spark performance we then propose a number of practical techniques to alleviate some of its overheads. However, optimizing computational efficiency and framework related overheads is not the only key to performance -- we demonstrate that in order to get the best performance out of any implementation it is necessary to carefully tune the algorithm to the respective trade-off between computation time and communication latency. The optimal trade-off depends on both the properties of the distributed algorithm as well as infrastructure and framework-related characteristics. Finally, we apply these technical and algorithmic optimizations to three different distributed linear machine learning algorithms that have been implemented in Spark. We present results using five large datasets and demonstrate that by using the proposed optimizations, we can achieve a reduction in the performance difference between Spark and MPI from 20x to 2x.
Efficient Use of Limited-Memory Accelerators for Linear Learning on Heterogeneous Systems
Nov 07, 2017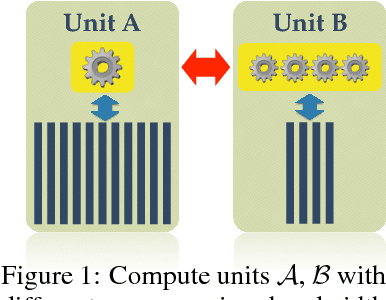
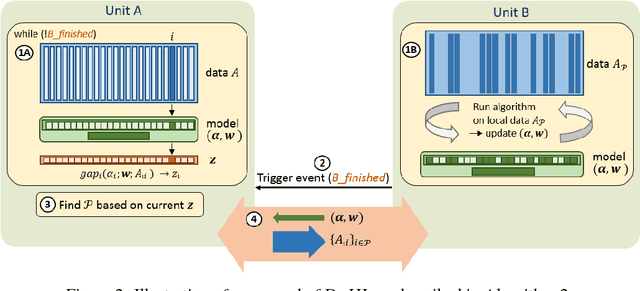
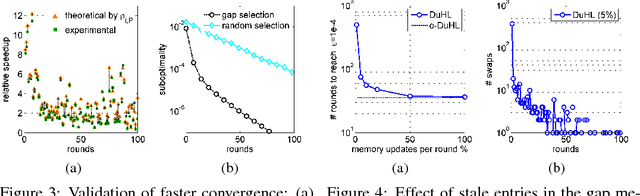
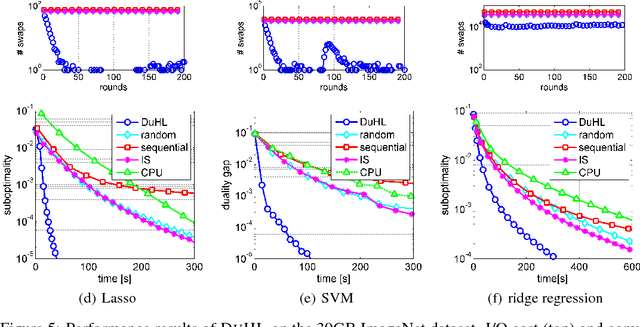
Abstract:We propose a generic algorithmic building block to accelerate training of machine learning models on heterogeneous compute systems. Our scheme allows to efficiently employ compute accelerators such as GPUs and FPGAs for the training of large-scale machine learning models, when the training data exceeds their memory capacity. Also, it provides adaptivity to any system's memory hierarchy in terms of size and processing speed. Our technique is built upon novel theoretical insights regarding primal-dual coordinate methods, and uses duality gap information to dynamically decide which part of the data should be made available for fast processing. To illustrate the power of our approach we demonstrate its performance for training of generalized linear models on a large-scale dataset exceeding the memory size of a modern GPU, showing an order-of-magnitude speedup over existing approaches.
Large-Scale Stochastic Learning using GPUs
Feb 22, 2017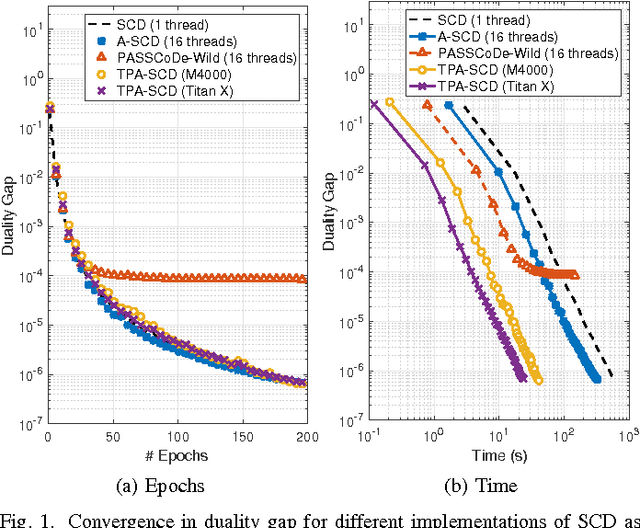
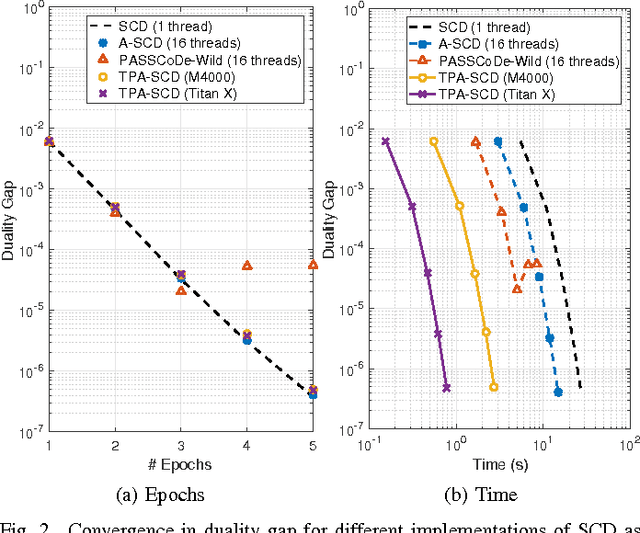
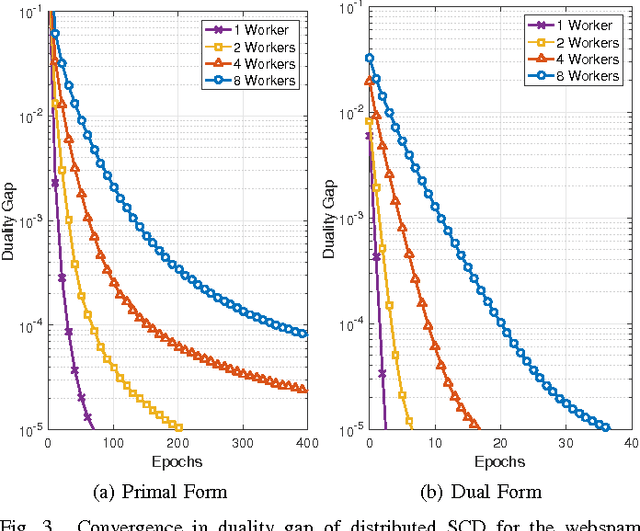
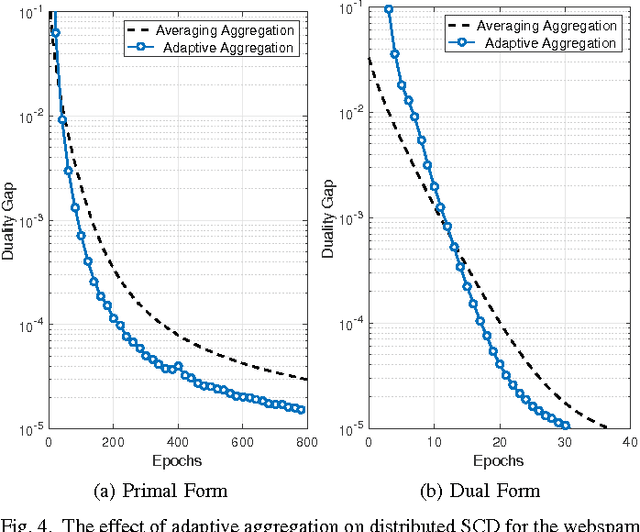
Abstract:In this work we propose an accelerated stochastic learning system for very large-scale applications. Acceleration is achieved by mapping the training algorithm onto massively parallel processors: we demonstrate a parallel, asynchronous GPU implementation of the widely used stochastic coordinate descent/ascent algorithm that can provide up to 35x speed-up over a sequential CPU implementation. In order to train on very large datasets that do not fit inside the memory of a single GPU, we then consider techniques for distributed stochastic learning. We propose a novel method for optimally aggregating model updates from worker nodes when the training data is distributed either by example or by feature. Using this technique, we demonstrate that one can scale out stochastic learning across up to 8 worker nodes without any significant loss of training time. Finally, we combine GPU acceleration with the optimized distributed method to train on a dataset consisting of 200 million training examples and 75 million features. We show by scaling out across 4 GPUs, one can attain a high degree of training accuracy in around 4 seconds: a 20x speed-up in training time compared to a multi-threaded, distributed implementation across 4 CPUs.
Primal-Dual Rates and Certificates
Jun 02, 2016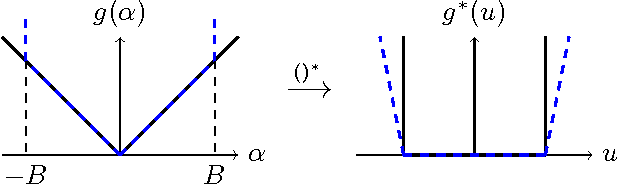

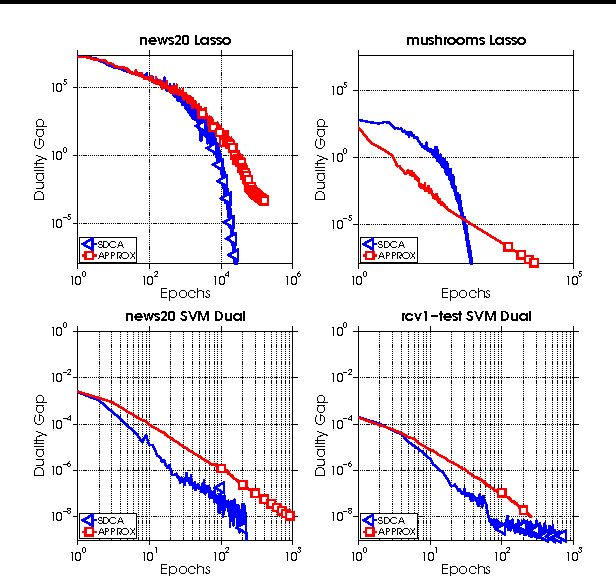
Abstract:We propose an algorithm-independent framework to equip existing optimization methods with primal-dual certificates. Such certificates and corresponding rate of convergence guarantees are important for practitioners to diagnose progress, in particular in machine learning applications. We obtain new primal-dual convergence rates, e.g., for the Lasso as well as many L1, Elastic Net, group Lasso and TV-regularized problems. The theory applies to any norm-regularized generalized linear model. Our approach provides efficiently computable duality gaps which are globally defined, without modifying the original problems in the region of interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge