Simone Forte
CoCoA: A General Framework for Communication-Efficient Distributed Optimization
Oct 10, 2018



Abstract:The scale of modern datasets necessitates the development of efficient distributed optimization methods for machine learning. We present a general-purpose framework for distributed computing environments, CoCoA, that has an efficient communication scheme and is applicable to a wide variety of problems in machine learning and signal processing. We extend the framework to cover general non-strongly-convex regularizers, including L1-regularized problems like lasso, sparse logistic regression, and elastic net regularization, and show how earlier work can be derived as a special case. We provide convergence guarantees for the class of convex regularized loss minimization objectives, leveraging a novel approach in handling non-strongly-convex regularizers and non-smooth loss functions. The resulting framework has markedly improved performance over state-of-the-art methods, as we illustrate with an extensive set of experiments on real distributed datasets.
L1-Regularized Distributed Optimization: A Communication-Efficient Primal-Dual Framework
Jun 02, 2016
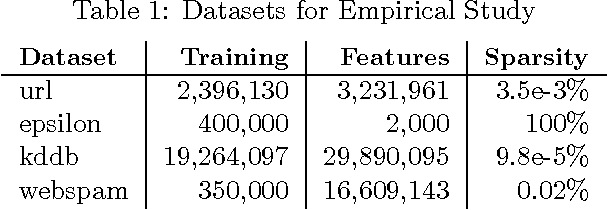
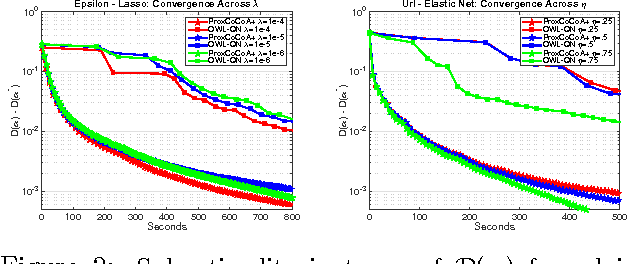
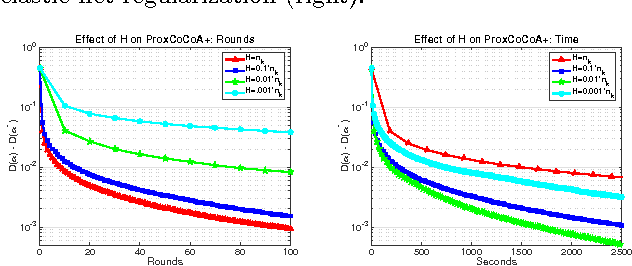
Abstract:Despite the importance of sparsity in many large-scale applications, there are few methods for distributed optimization of sparsity-inducing objectives. In this paper, we present a communication-efficient framework for L1-regularized optimization in the distributed environment. By viewing classical objectives in a more general primal-dual setting, we develop a new class of methods that can be efficiently distributed and applied to common sparsity-inducing models, such as Lasso, sparse logistic regression, and elastic net-regularized problems. We provide theoretical convergence guarantees for our framework, and demonstrate its efficiency and flexibility with a thorough experimental comparison on Amazon EC2. Our proposed framework yields speedups of up to 50x as compared to current state-of-the-art methods for distributed L1-regularized optimization.
Primal-Dual Rates and Certificates
Jun 02, 2016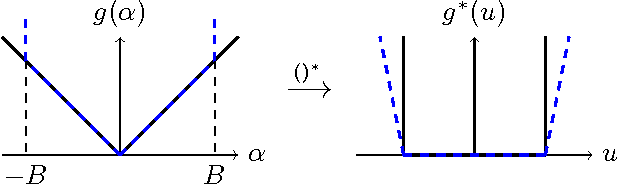

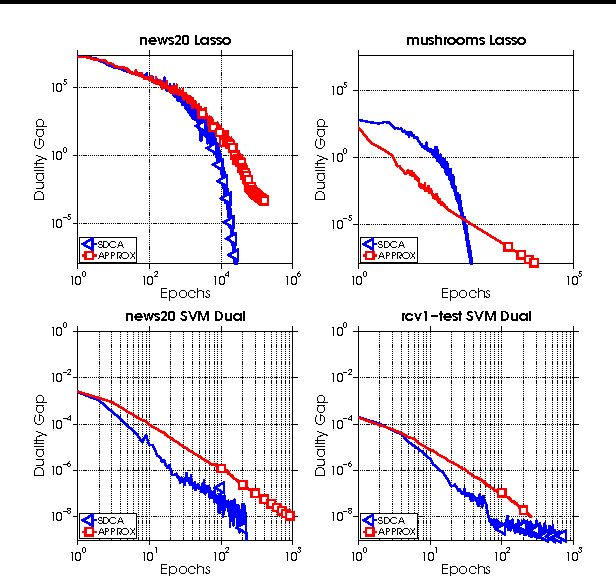
Abstract:We propose an algorithm-independent framework to equip existing optimization methods with primal-dual certificates. Such certificates and corresponding rate of convergence guarantees are important for practitioners to diagnose progress, in particular in machine learning applications. We obtain new primal-dual convergence rates, e.g., for the Lasso as well as many L1, Elastic Net, group Lasso and TV-regularized problems. The theory applies to any norm-regularized generalized linear model. Our approach provides efficiently computable duality gaps which are globally defined, without modifying the original problems in the region of interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge