Efficient Distributed Hessian Free Algorithm for Large-scale Empirical Risk Minimization via Accumulating Sample Strategy

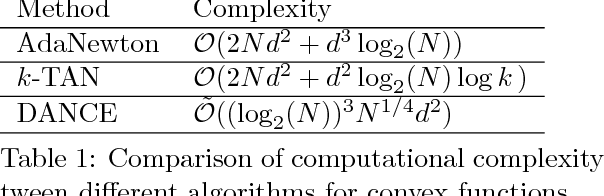
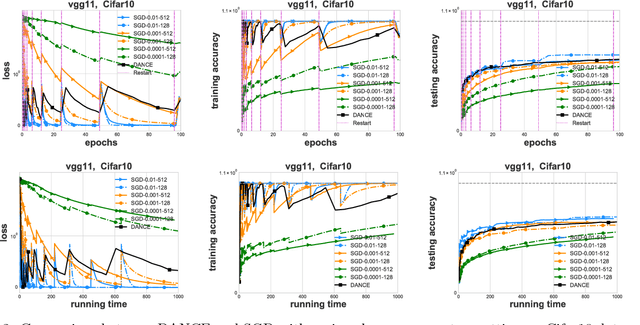
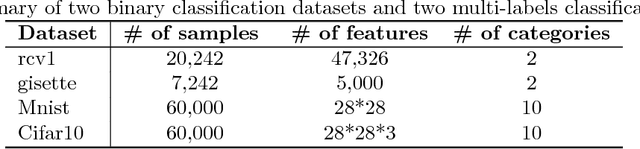
In this paper, we propose a Distributed Accumulated Newton Conjugate gradiEnt (DANCE) method in which sample size is gradually increasing to quickly obtain a solution whose empirical loss is under satisfactory statistical accuracy. Our proposed method is multistage in which the solution of a stage serves as a warm start for the next stage which contains more samples (including the samples in the previous stage). The proposed multistage algorithm reduces the number of passes over data to achieve the statistical accuracy of the full training set. Moreover, our algorithm in nature is easy to be distributed and shares the strong scaling property indicating that acceleration is always expected by using more computing nodes. Various iteration complexity results regarding descent direction computation, communication efficiency and stopping criteria are analyzed under convex setting. Our numerical results illustrate that the proposed method outperforms other comparable methods for solving learning problems including neural networks.

CoCoA: A General Framework for Communication-Efficient Distributed Optimization

The scale of modern datasets necessitates the development of efficient distributed optimization methods for machine learning. We present a general-purpose framework for distributed computing environments, CoCoA, that has an efficient communication scheme and is applicable to a wide variety of problems in machine learning and signal processing. We extend the framework to cover general non-strongly-convex regularizers, including L1-regularized problems like lasso, sparse logistic regression, and elastic net regularization, and show how earlier work can be derived as a special case. We provide convergence guarantees for the class of convex regularized loss minimization objectives, leveraging a novel approach in handling non-strongly-convex regularizers and non-smooth loss functions. The resulting framework has markedly improved performance over state-of-the-art methods, as we illustrate with an extensive set of experiments on real distributed datasets.

An Accelerated Communication-Efficient Primal-Dual Optimization Framework for Structured Machine Learning

Distributed optimization algorithms are essential for training machine learning models on very large-scale datasets. However, they often suffer from communication bottlenecks. Confronting this issue, a communication-efficient primal-dual coordinate ascent framework (CoCoA) and its improved variant CoCoA+ have been proposed, achieving a convergence rate of $\mathcal{O}(1/t)$ for solving empirical risk minimization problems with Lipschitz continuous losses. In this paper, an accelerated variant of CoCoA+ is proposed and shown to possess a convergence rate of $\mathcal{O}(1/t^2)$ in terms of reducing suboptimality. The analysis of this rate is also notable in that the convergence rate bounds involve constants that, except in extreme cases, are significantly reduced compared to those previously provided for CoCoA+. The results of numerical experiments are provided to show that acceleration can lead to significant performance gains.

Underestimate Sequences via Quadratic Averaging

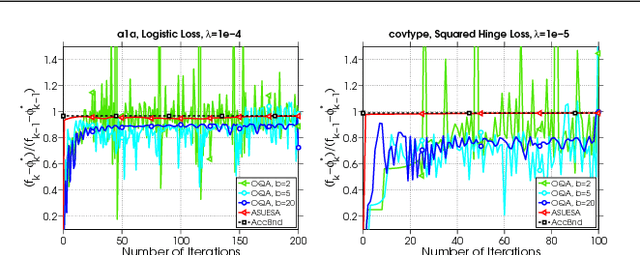
In this work we introduce the concept of an Underestimate Sequence (UES), which is a natural extension of Nesterov's estimate sequence. Our definition of a UES utilizes three sequences, one of which is a lower bound (or under-estimator) of the objective function. The question of how to construct an appropriate sequence of lower bounds is also addressed, and we present lower bounds for strongly convex smooth functions and for strongly convex composite functions, which adhere to the UES framework. Further, we propose several first order methods for minimizing strongly convex functions in both the smooth and composite cases. The algorithms, based on efficiently updating lower bounds on the objective functions, have natural stopping conditions, which provides the user with a certificate of optimality. Convergence of all algorithms is guaranteed through the UES framework, and we show that all presented algorithms converge linearly, with the accelerated variants enjoying the optimal linear rate of convergence.

Distributed Optimization with Arbitrary Local Solvers

With the growth of data and necessity for distributed optimization methods, solvers that work well on a single machine must be re-designed to leverage distributed computation. Recent work in this area has been limited by focusing heavily on developing highly specific methods for the distributed environment. These special-purpose methods are often unable to fully leverage the competitive performance of their well-tuned and customized single machine counterparts. Further, they are unable to easily integrate improvements that continue to be made to single machine methods. To this end, we present a framework for distributed optimization that both allows the flexibility of arbitrary solvers to be used on each (single) machine locally, and yet maintains competitive performance against other state-of-the-art special-purpose distributed methods. We give strong primal-dual convergence rate guarantees for our framework that hold for arbitrary local solvers. We demonstrate the impact of local solver selection both theoretically and in an extensive experimental comparison. Finally, we provide thorough implementation details for our framework, highlighting areas for practical performance gains.

Distributed Inexact Damped Newton Method: Data Partitioning and Load-Balancing

In this paper we study inexact dumped Newton method implemented in a distributed environment. We start with an original DiSCO algorithm [Communication-Efficient Distributed Optimization of Self-Concordant Empirical Loss, Yuchen Zhang and Lin Xiao, 2015]. We will show that this algorithm may not scale well and propose an algorithmic modifications which will lead to less communications, better load-balancing and more efficient computation. We perform numerical experiments with an regularized empirical loss minimization instance described by a 273GB dataset.

Partitioning Data on Features or Samples in Communication-Efficient Distributed Optimization?

In this paper we study the effect of the way that the data is partitioned in distributed optimization. The original DiSCO algorithm [Communication-Efficient Distributed Optimization of Self-Concordant Empirical Loss, Yuchen Zhang and Lin Xiao, 2015] partitions the input data based on samples. We describe how the original algorithm has to be modified to allow partitioning on features and show its efficiency both in theory and also in practice.

Adding vs. Averaging in Distributed Primal-Dual Optimization

Distributed optimization methods for large-scale machine learning suffer from a communication bottleneck. It is difficult to reduce this bottleneck while still efficiently and accurately aggregating partial work from different machines. In this paper, we present a novel generalization of the recent communication-efficient primal-dual framework (CoCoA) for distributed optimization. Our framework, CoCoA+, allows for additive combination of local updates to the global parameters at each iteration, whereas previous schemes with convergence guarantees only allow conservative averaging. We give stronger (primal-dual) convergence rate guarantees for both CoCoA as well as our new variants, and generalize the theory for both methods to cover non-smooth convex loss functions. We provide an extensive experimental comparison that shows the markedly improved performance of CoCoA+ on several real-world distributed datasets, especially when scaling up the number of machines.

Linear Convergence of the Randomized Feasible Descent Method Under the Weak Strong Convexity Assumption

In this paper we generalize the framework of the feasible descent method (FDM) to a randomized (R-FDM) and a coordinate-wise random feasible descent method (RC-FDM) framework. We show that the famous SDCA algorithm for optimizing the SVM dual problem, or the stochastic coordinate descent method for the LASSO problem, fits into the framework of RC-FDM. We prove linear convergence for both R-FDM and RC-FDM under the weak strong convexity assumption. Moreover, we show that the duality gap converges linearly for RC-FDM, which implies that the duality gap also converges linearly for SDCA applied to the SVM dual problem.