L1-Regularized Distributed Optimization: A Communication-Efficient Primal-Dual Framework
Paper and Code
Jun 02, 2016
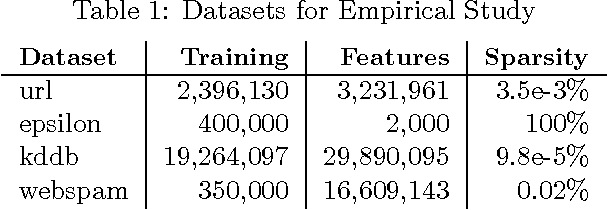
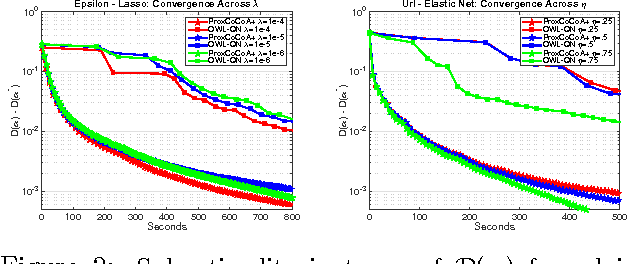
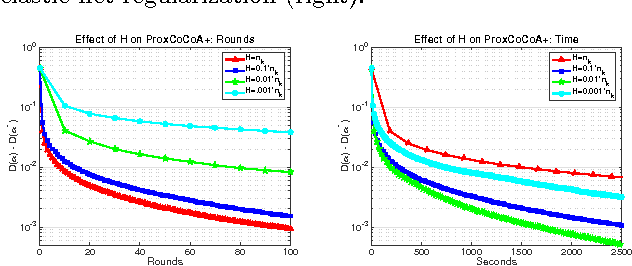
Despite the importance of sparsity in many large-scale applications, there are few methods for distributed optimization of sparsity-inducing objectives. In this paper, we present a communication-efficient framework for L1-regularized optimization in the distributed environment. By viewing classical objectives in a more general primal-dual setting, we develop a new class of methods that can be efficiently distributed and applied to common sparsity-inducing models, such as Lasso, sparse logistic regression, and elastic net-regularized problems. We provide theoretical convergence guarantees for our framework, and demonstrate its efficiency and flexibility with a thorough experimental comparison on Amazon EC2. Our proposed framework yields speedups of up to 50x as compared to current state-of-the-art methods for distributed L1-regularized optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge