An Bian
COLA: Decentralized Linear Learning
Oct 29, 2018



Abstract:Decentralized machine learning is a promising emerging paradigm in view of global challenges of data ownership and privacy. We consider learning of linear classification and regression models, in the setting where the training data is decentralized over many user devices, and the learning algorithm must run on-device, on an arbitrary communication network, without a central coordinator. We propose COLA, a new decentralized training algorithm with strong theoretical guarantees and superior practical performance. Our framework overcomes many limitations of existing methods, and achieves communication efficiency, scalability, elasticity as well as resilience to changes in data and participating devices.
A Distributed Second-Order Algorithm You Can Trust
Jun 20, 2018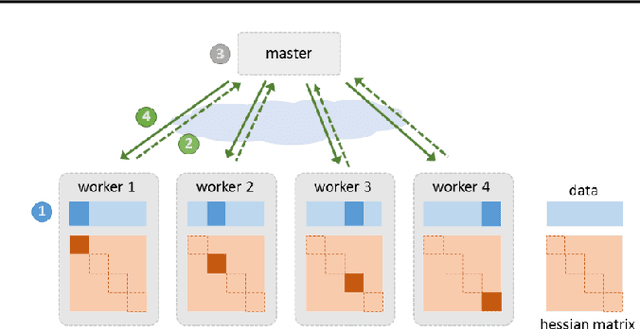
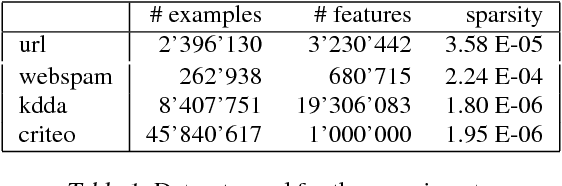
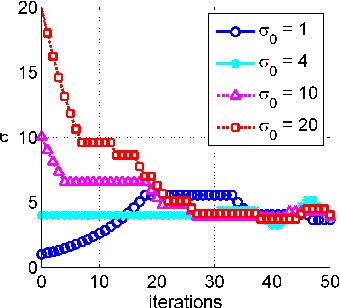
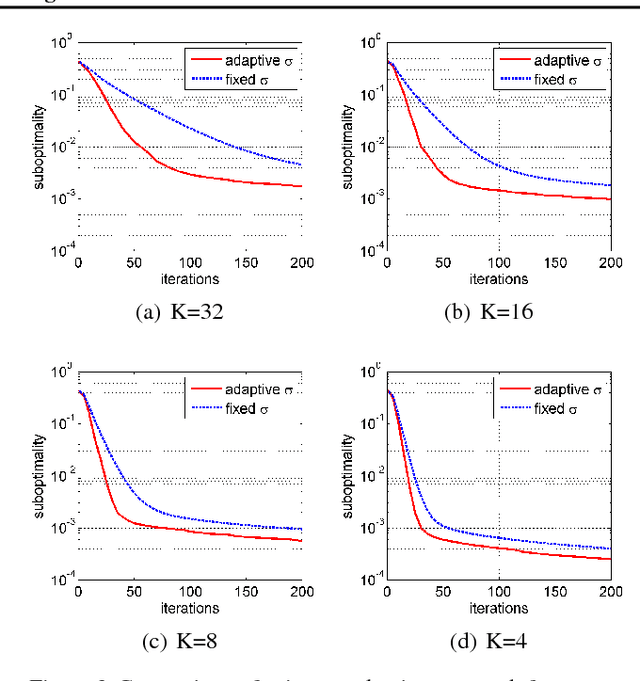
Abstract:Due to the rapid growth of data and computational resources, distributed optimization has become an active research area in recent years. While first-order methods seem to dominate the field, second-order methods are nevertheless attractive as they potentially require fewer communication rounds to converge. However, there are significant drawbacks that impede their wide adoption, such as the computation and the communication of a large Hessian matrix. In this paper we present a new algorithm for distributed training of generalized linear models that only requires the computation of diagonal blocks of the Hessian matrix on the individual workers. To deal with this approximate information we propose an adaptive approach that - akin to trust-region methods - dynamically adapts the auxiliary model to compensate for modeling errors. We provide theoretical rates of convergence for a wide class of problems including L1-regularized objectives. We also demonstrate that our approach achieves state-of-the-art results on multiple large benchmark datasets.
Optimal DR-Submodular Maximization and Applications to Provable Mean Field Inference
May 19, 2018

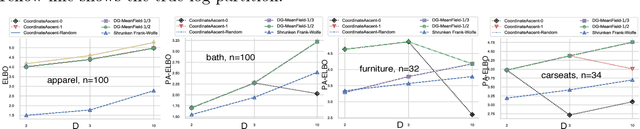
Abstract:Mean field inference in probabilistic models is generally a highly nonconvex problem. Existing optimization methods, e.g., coordinate ascent algorithms, can only generate local optima. In this work we propose provable mean filed methods for probabilistic log-submodular models and its posterior agreement (PA) with strong approximation guarantees. The main algorithmic technique is a new Double Greedy scheme, termed DR-DoubleGreedy, for continuous DR-submodular maximization with box-constraints. It is a one-pass algorithm with linear time complexity, reaching the optimal 1/2 approximation ratio, which may be of independent interest. We validate the superior performance of our algorithms against baseline algorithms on both synthetic and real-world datasets.
Continuous DR-submodular Maximization: Structure and Algorithms
Dec 16, 2017



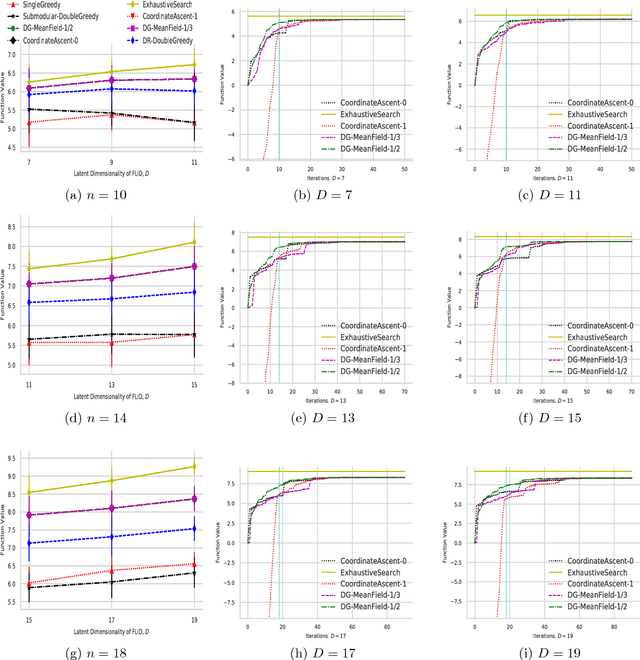
Abstract:DR-submodular continuous functions are important objectives with wide real-world applications spanning MAP inference in determinantal point processes (DPPs), and mean-field inference for probabilistic submodular models, amongst others. DR-submodularity captures a subclass of non-convex functions that enables both exact minimization and approximate maximization in polynomial time. In this work we study the problem of maximizing non-monotone DR-submodular continuous functions under general down-closed convex constraints. We start by investigating geometric properties that underlie such objectives, e.g., a strong relation between (approximately) stationary points and global optimum is proved. These properties are then used to devise two optimization algorithms with provable guarantees. Concretely, we first devise a "two-phase" algorithm with $1/4$ approximation guarantee. This algorithm allows the use of existing methods for finding (approximately) stationary points as a subroutine, thus, harnessing recent progress in non-convex optimization. Then we present a non-monotone Frank-Wolfe variant with $1/e$ approximation guarantee and sublinear convergence rate. Finally, we extend our approach to a broader class of generalized DR-submodular continuous functions, which captures a wider spectrum of applications. Our theoretical findings are validated on synthetic and real-world problem instances.
Parallel Coordinate Descent Newton Method for Efficient $\ell_1$-Regularized Minimization
Dec 07, 2017
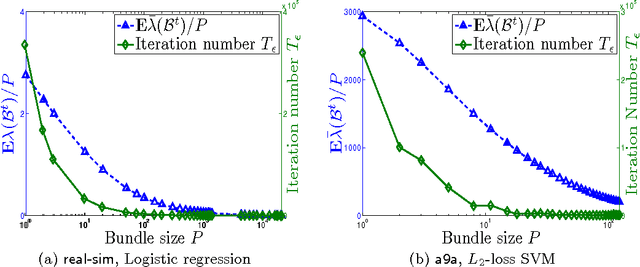

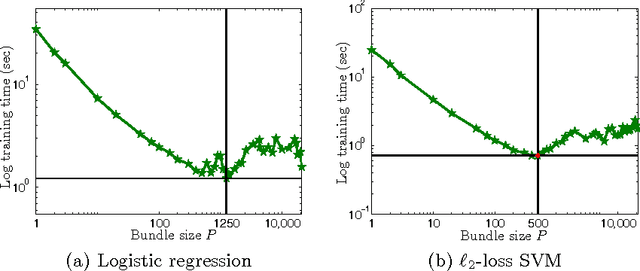
Abstract:The recent years have witnessed advances in parallel algorithms for large scale optimization problems. Notwithstanding demonstrated success, existing algorithms that parallelize over features are usually limited by divergence issues under high parallelism or require data preprocessing to alleviate these problems. In this work, we propose a Parallel Coordinate Descent Newton algorithm using multidimensional approximate Newton steps (PCDN), where the off-diagonal elements of the Hessian are set to zero to enable parallelization. It randomly partitions the feature set into $b$ bundles/subsets with size of $P$, and sequentially processes each bundle by first computing the descent directions for each feature in parallel and then conducting $P$-dimensional line search to obtain the step size. We show that: (1) PCDN is guaranteed to converge globally despite increasing parallelism; (2) PCDN converges to the specified accuracy $\epsilon$ within the limited iteration number of $T_\epsilon$, and $T_\epsilon$ decreases with increasing parallelism (bundle size $P$). Using the implementation technique of maintaining intermediate quantities, we minimize the data transfer and synchronization cost of the $P$-dimensional line search. For concreteness, the proposed PCDN algorithm is applied to $\ell_1$-regularized logistic regression and $\ell_2$-loss SVM. Experimental evaluations on six benchmark datasets show that the proposed PCDN algorithm exploits parallelism well and outperforms the state-of-the-art methods in speed without losing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge