Parallel Coordinate Descent Newton Method for Efficient $\ell_1$-Regularized Minimization

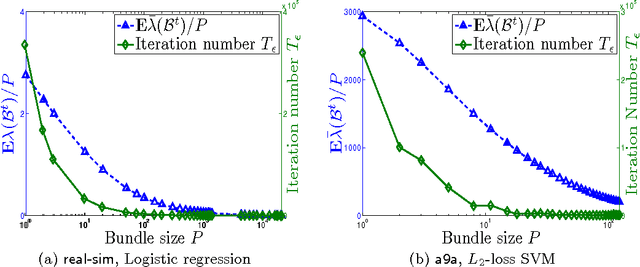
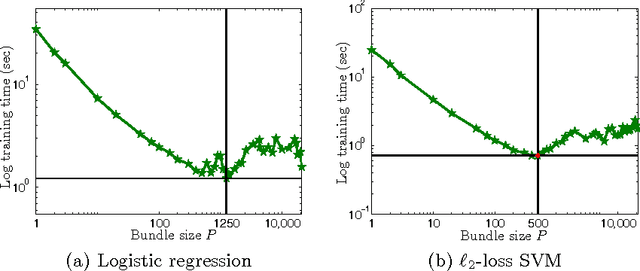
The recent years have witnessed advances in parallel algorithms for large scale optimization problems. Notwithstanding demonstrated success, existing algorithms that parallelize over features are usually limited by divergence issues under high parallelism or require data preprocessing to alleviate these problems. In this work, we propose a Parallel Coordinate Descent Newton algorithm using multidimensional approximate Newton steps (PCDN), where the off-diagonal elements of the Hessian are set to zero to enable parallelization. It randomly partitions the feature set into $b$ bundles/subsets with size of $P$, and sequentially processes each bundle by first computing the descent directions for each feature in parallel and then conducting $P$-dimensional line search to obtain the step size. We show that: (1) PCDN is guaranteed to converge globally despite increasing parallelism; (2) PCDN converges to the specified accuracy $\epsilon$ within the limited iteration number of $T_\epsilon$, and $T_\epsilon$ decreases with increasing parallelism (bundle size $P$). Using the implementation technique of maintaining intermediate quantities, we minimize the data transfer and synchronization cost of the $P$-dimensional line search. For concreteness, the proposed PCDN algorithm is applied to $\ell_1$-regularized logistic regression and $\ell_2$-loss SVM. Experimental evaluations on six benchmark datasets show that the proposed PCDN algorithm exploits parallelism well and outperforms the state-of-the-art methods in speed without losing accuracy.

Stochastic Feature Mapping for PAC-Bayes Classification

Probabilistic generative modeling of data distributions can potentially exploit hidden information which is useful for discriminative classification. This observation has motivated the development of approaches that couple generative and discriminative models for classification. In this paper, we propose a new approach to couple generative and discriminative models in an unified framework based on PAC-Bayes risk theory. We first derive the model-parameter-independent stochastic feature mapping from a practical MAP classifier operating on generative models. Then we construct a linear stochastic classifier equipped with the feature mapping, and derive the explicit PAC-Bayes risk bounds for such classifier for both supervised and semi-supervised learning. Minimizing the risk bound, using an EM-like iterative procedure, results in a new posterior over hidden variables (E-step) and the update rules of model parameters (M-step). The derivation of the posterior is always feasible due to the way of equipping feature mapping and the explicit form of bounding risk. The derived posterior allows the tuning of generative models and subsequently the feature mappings for better classification. The derived update rules of the model parameters are same to those of the uncoupled models as the feature mapping is model-parameter-independent. Our experiments show that the coupling between data modeling generative model and the discriminative classifier via a stochastic feature mapping in this framework leads to a general classification tool with state-of-the-art performance.