Parallel Coordinate Descent Newton Method for Efficient $\ell_1$-Regularized Minimization
Paper and Code
Dec 07, 2017
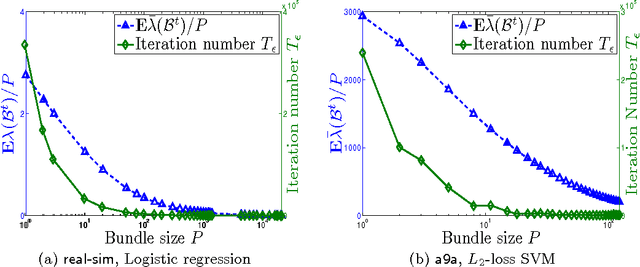
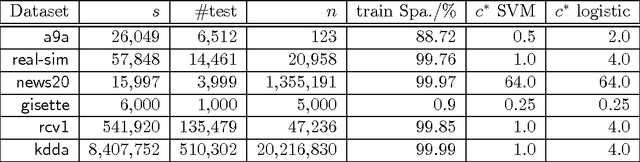
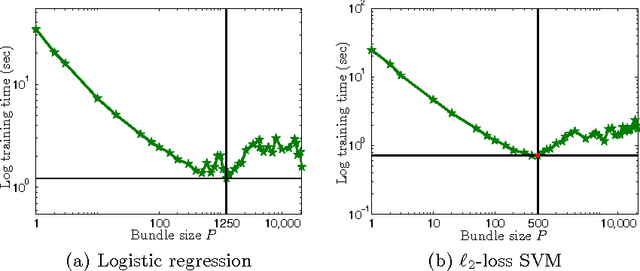
The recent years have witnessed advances in parallel algorithms for large scale optimization problems. Notwithstanding demonstrated success, existing algorithms that parallelize over features are usually limited by divergence issues under high parallelism or require data preprocessing to alleviate these problems. In this work, we propose a Parallel Coordinate Descent Newton algorithm using multidimensional approximate Newton steps (PCDN), where the off-diagonal elements of the Hessian are set to zero to enable parallelization. It randomly partitions the feature set into $b$ bundles/subsets with size of $P$, and sequentially processes each bundle by first computing the descent directions for each feature in parallel and then conducting $P$-dimensional line search to obtain the step size. We show that: (1) PCDN is guaranteed to converge globally despite increasing parallelism; (2) PCDN converges to the specified accuracy $\epsilon$ within the limited iteration number of $T_\epsilon$, and $T_\epsilon$ decreases with increasing parallelism (bundle size $P$). Using the implementation technique of maintaining intermediate quantities, we minimize the data transfer and synchronization cost of the $P$-dimensional line search. For concreteness, the proposed PCDN algorithm is applied to $\ell_1$-regularized logistic regression and $\ell_2$-loss SVM. Experimental evaluations on six benchmark datasets show that the proposed PCDN algorithm exploits parallelism well and outperforms the state-of-the-art methods in speed without losing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge