PAGE-PG: A Simple and Loopless Variance-Reduced Policy Gradient Method with Probabilistic Gradient Estimation

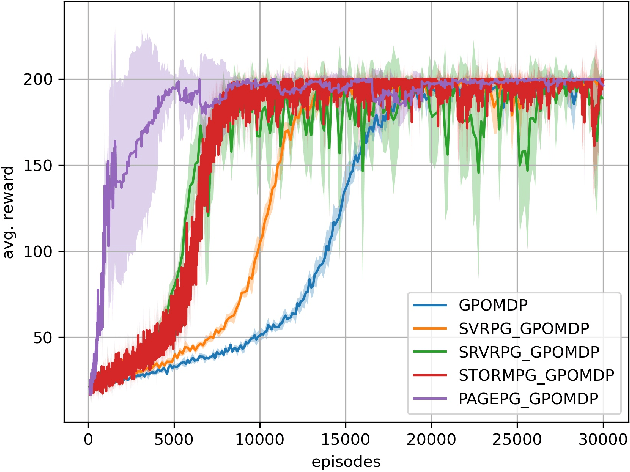
Despite their success, policy gradient methods suffer from high variance of the gradient estimate, which can result in unsatisfactory sample complexity. Recently, numerous variance-reduced extensions of policy gradient methods with provably better sample complexity and competitive numerical performance have been proposed. After a compact survey on some of the main variance-reduced REINFORCE-type methods, we propose ProbAbilistic Gradient Estimation for Policy Gradient (PAGE-PG), a novel loopless variance-reduced policy gradient method based on a probabilistic switch between two types of updates. Our method is inspired by the PAGE estimator for supervised learning and leverages importance sampling to obtain an unbiased gradient estimator. We show that PAGE-PG enjoys a $\mathcal{O}\left( \epsilon^{-3} \right)$ average sample complexity to reach an $\epsilon$-stationary solution, which matches the sample complexity of its most competitive counterparts under the same setting. A numerical evaluation confirms the competitive performance of our method on classical control tasks.

Convergence Analysis of Homotopy-SGD for non-convex optimization

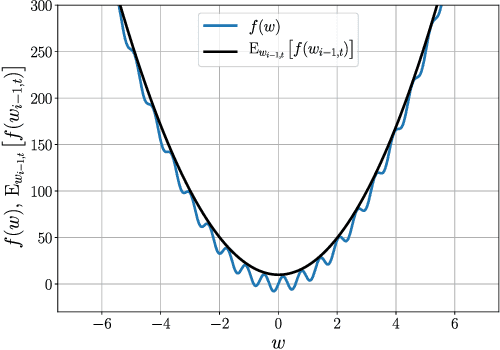
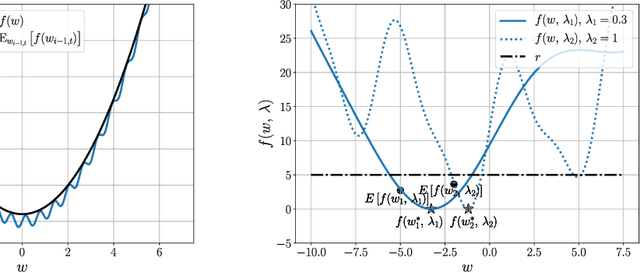
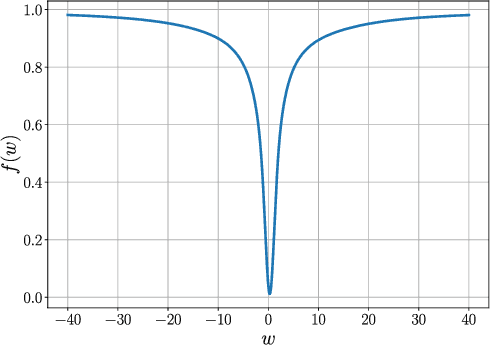
First-order stochastic methods for solving large-scale non-convex optimization problems are widely used in many big-data applications, e.g. training deep neural networks as well as other complex and potentially non-convex machine learning models. Their inexpensive iterations generally come together with slow global convergence rate (mostly sublinear), leading to the necessity of carrying out a very high number of iterations before the iterates reach a neighborhood of a minimizer. In this work, we present a first-order stochastic algorithm based on a combination of homotopy methods and SGD, called Homotopy-Stochastic Gradient Descent (H-SGD), which finds interesting connections with some proposed heuristics in the literature, e.g. optimization by Gaussian continuation, training by diffusion, mollifying networks. Under some mild assumptions on the problem structure, we conduct a theoretical analysis of the proposed algorithm. Our analysis shows that, with a specifically designed scheme for the homotopy parameter, H-SGD enjoys a global linear rate of convergence to a neighborhood of a minimum while maintaining fast and inexpensive iterations. Experimental evaluations confirm the theoretical results and show that H-SGD can outperform standard SGD.

On the Promise of the Stochastic Generalized Gauss-Newton Method for Training DNNs

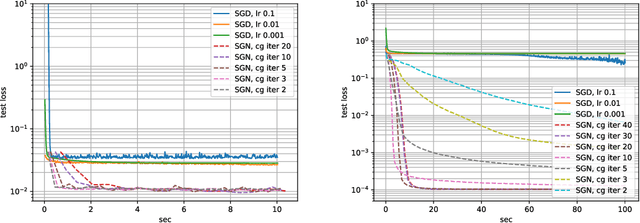
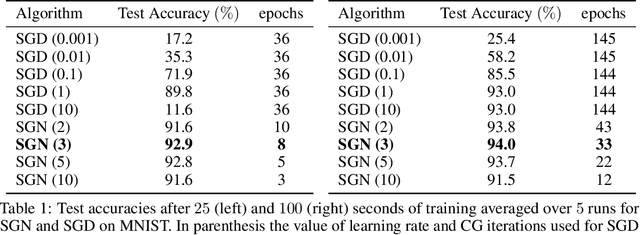
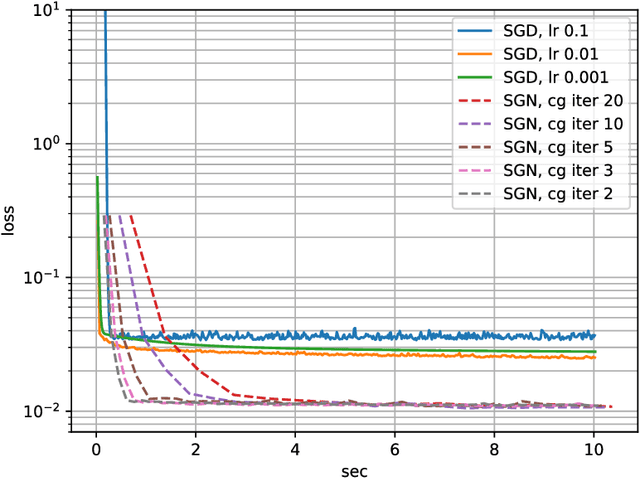
Following early work on Hessian-free methods for deep learning, we study a stochastic generalized Gauss-Newton method (SGN) for training DNNs. SGN is a second-order optimization method, with efficient iterations, that we demonstrate to often require substantially fewer iterations than standard SGD to converge. As the name suggests, SGN uses a Gauss-Newton approximation for the Hessian matrix, and, in order to compute an approximate search direction, relies on the conjugate gradient method combined with forward and reverse automatic differentiation. Despite the success of SGD and its first-order variants, and despite Hessian-free methods based on the Gauss-Newton Hessian approximation having been already theoretically proposed as practical methods for training DNNs, we believe that SGN has a lot of undiscovered and yet not fully displayed potential in big mini-batch scenarios. For this setting, we demonstrate that SGN does not only substantially improve over SGD in terms of the number of iterations, but also in terms of runtime. This is made possible by an efficient, easy-to-use and flexible implementation of SGN we propose in the Theano deep learning platform, which, unlike Tensorflow and Pytorch, supports forward automatic differentiation. This enables researchers to further study and improve this promising optimization technique and hopefully reconsider stochastic second-order methods as competitive optimization techniques for training DNNs; we also hope that the promise of SGN may lead to forward automatic differentiation being added to Tensorflow or Pytorch. Our results also show that in big mini-batch scenarios SGN is more robust than SGD with respect to its hyperparameters (we never had to tune its step-size for our benchmarks!), which eases the expensive process of hyperparameter tuning that is instead crucial for the performance of first-order methods.

Probabilistic Rollouts for Learning Curve Extrapolation Across Hyperparameter Settings

We propose probabilistic models that can extrapolate learning curves of iterative machine learning algorithms, such as stochastic gradient descent for training deep networks, based on training data with variable-length learning curves. We study instantiations of this framework based on random forests and Bayesian recurrent neural networks. Our experiments show that these models yield better predictions than state-of-the-art models from the hyperparameter optimization literature when extrapolating the performance of neural networks trained with different hyperparameter settings.

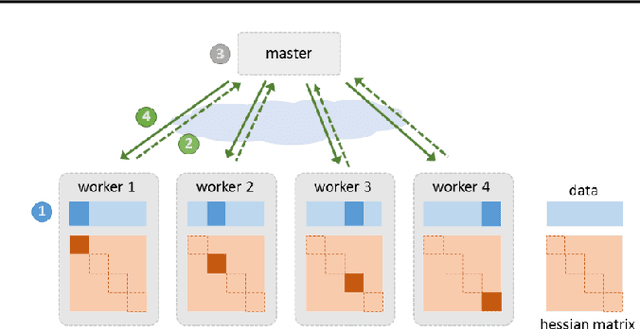
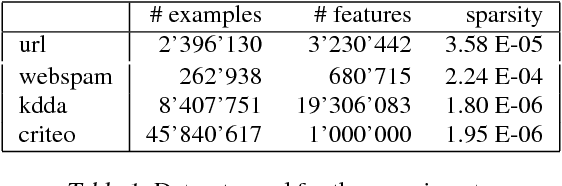
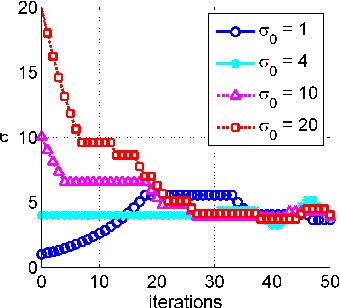
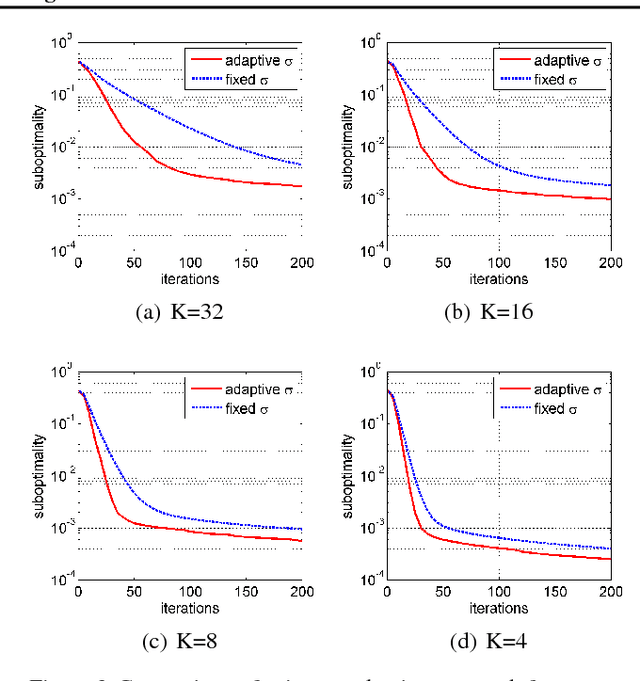
A Distributed Second-Order Algorithm You Can Trust

Due to the rapid growth of data and computational resources, distributed optimization has become an active research area in recent years. While first-order methods seem to dominate the field, second-order methods are nevertheless attractive as they potentially require fewer communication rounds to converge. However, there are significant drawbacks that impede their wide adoption, such as the computation and the communication of a large Hessian matrix. In this paper we present a new algorithm for distributed training of generalized linear models that only requires the computation of diagonal blocks of the Hessian matrix on the individual workers. To deal with this approximate information we propose an adaptive approach that - akin to trust-region methods - dynamically adapts the auxiliary model to compensate for modeling errors. We provide theoretical rates of convergence for a wide class of problems including L1-regularized objectives. We also demonstrate that our approach achieves state-of-the-art results on multiple large benchmark datasets.