Inherently robust suboptimal MPC for autonomous racing with anytime feasible SQP

In recent years, the increasing need for high-performance controllers in applications like autonomous driving has motivated the development of optimization routines tailored to specific control problems. In this paper, we propose an efficient inexact model predictive control (MPC) strategy for autonomous miniature racing with inherent robustness properties. We rely on a feasible sequential quadratic programming (SQP) algorithm capable of generating feasible intermediate iterates such that the solver can be stopped after any number of iterations, without jeopardizing recursive feasibility. In this way, we provide a strategy that computes suboptimal and yet feasible solutions with a computational footprint that is much lower than state-of-the-art methods based on the computation of locally optimal solutions. Under suitable assumptions on the terminal set and on the controllability properties of the system, we can state that, for any sufficiently small disturbance affecting the system's dynamics, recursive feasibility can be guaranteed. We validate the effectiveness of the proposed strategy in simulation and by deploying it onto a physical experiment with autonomous miniature race cars. Both the simulation and experimental results demonstrate that, using the feasible SQP method, a feasible solution can be obtained with moderate additional computational effort compared to strategies that resort to early termination without providing a feasible solution. At the same time, the proposed method is significantly faster than the state-of-the-art solver Ipopt.

PAGE-PG: A Simple and Loopless Variance-Reduced Policy Gradient Method with Probabilistic Gradient Estimation

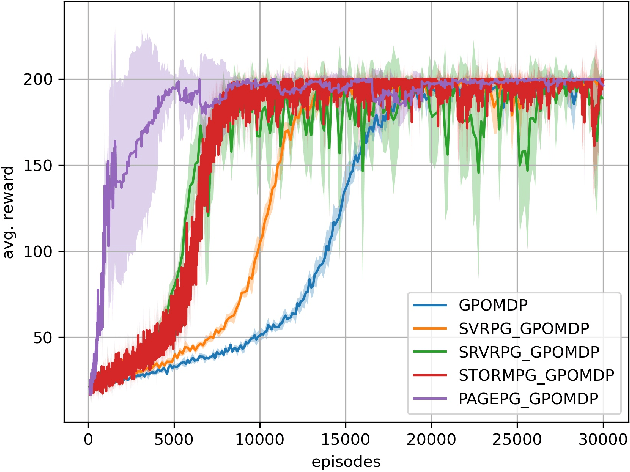
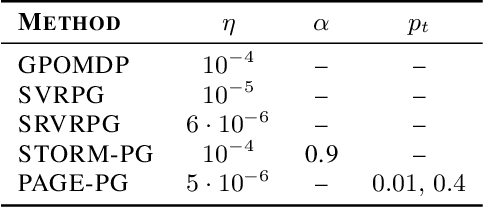
Despite their success, policy gradient methods suffer from high variance of the gradient estimate, which can result in unsatisfactory sample complexity. Recently, numerous variance-reduced extensions of policy gradient methods with provably better sample complexity and competitive numerical performance have been proposed. After a compact survey on some of the main variance-reduced REINFORCE-type methods, we propose ProbAbilistic Gradient Estimation for Policy Gradient (PAGE-PG), a novel loopless variance-reduced policy gradient method based on a probabilistic switch between two types of updates. Our method is inspired by the PAGE estimator for supervised learning and leverages importance sampling to obtain an unbiased gradient estimator. We show that PAGE-PG enjoys a $\mathcal{O}\left( \epsilon^{-3} \right)$ average sample complexity to reach an $\epsilon$-stationary solution, which matches the sample complexity of its most competitive counterparts under the same setting. A numerical evaluation confirms the competitive performance of our method on classical control tasks.

Convergence Analysis of Homotopy-SGD for non-convex optimization

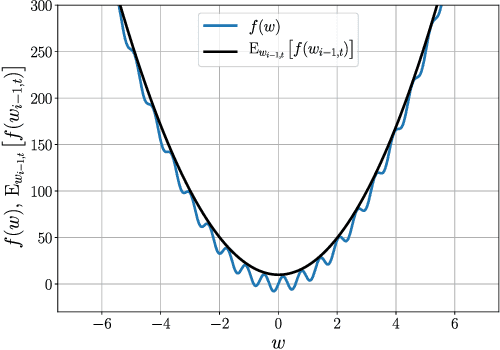
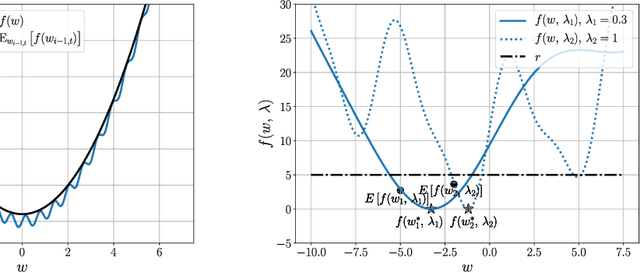
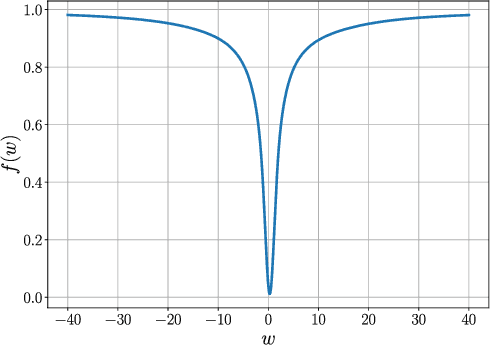
First-order stochastic methods for solving large-scale non-convex optimization problems are widely used in many big-data applications, e.g. training deep neural networks as well as other complex and potentially non-convex machine learning models. Their inexpensive iterations generally come together with slow global convergence rate (mostly sublinear), leading to the necessity of carrying out a very high number of iterations before the iterates reach a neighborhood of a minimizer. In this work, we present a first-order stochastic algorithm based on a combination of homotopy methods and SGD, called Homotopy-Stochastic Gradient Descent (H-SGD), which finds interesting connections with some proposed heuristics in the literature, e.g. optimization by Gaussian continuation, training by diffusion, mollifying networks. Under some mild assumptions on the problem structure, we conduct a theoretical analysis of the proposed algorithm. Our analysis shows that, with a specifically designed scheme for the homotopy parameter, H-SGD enjoys a global linear rate of convergence to a neighborhood of a minimum while maintaining fast and inexpensive iterations. Experimental evaluations confirm the theoretical results and show that H-SGD can outperform standard SGD.

An Efficient Real-Time NMPC for Quadrotor Position Control under Communication Time-Delay

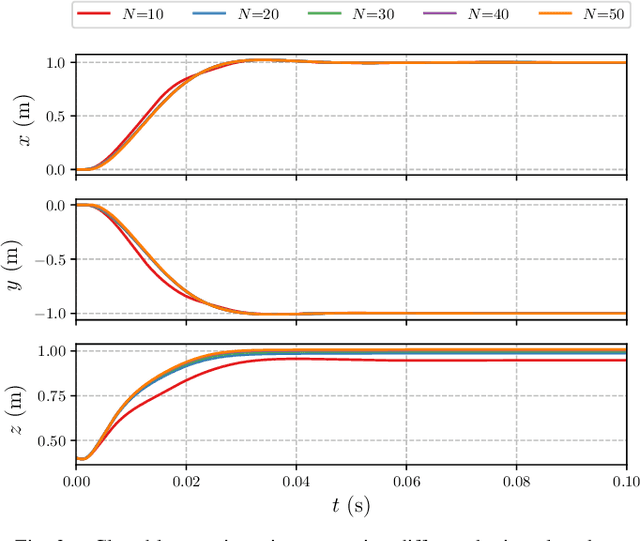
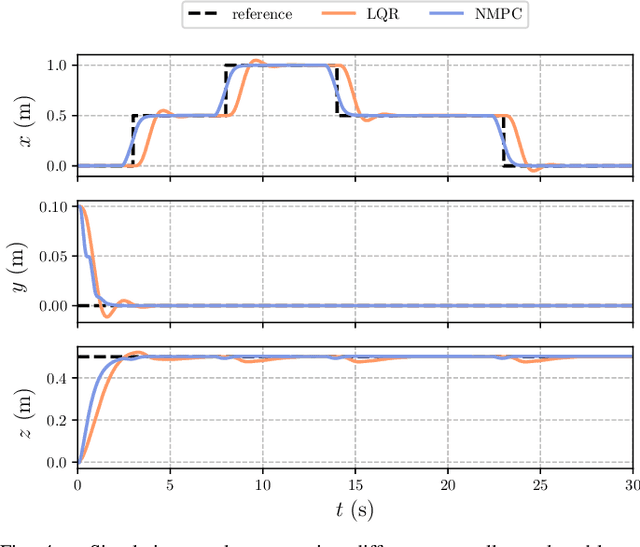
The advances in computer processor technology have enabled the application of nonlinear model predictive control (NMPC) to agile systems, such as quadrotors. These systems are characterized by their underactuation, nonlinearities, bounded inputs, and time-delays. Classical control solutions fall short in overcoming these difficulties and fully exploiting the capabilities offered by such platforms. This paper presents the design and implementation of an efficient position controller for quadrotors based on real-time NMPC with time-delay compensation and bounds enforcement on the actuators. To deal with the limited computational resources onboard, an offboard control architecture is proposed. It is implemented using the high-performance software package acados, which solves optimal control problems and implements a real-time iteration (RTI) variant of a sequential quadratic programming (SQP) scheme with Gauss-Newton Hessian approximation. The quadratic subproblems (QP) in the SQP scheme are solved with HPIPM, an interior-point method solver, built on top of the linear algebra library BLASFEO, finely tuned for multiple CPU architectures. Solution times are further reduced by reformulating the QPs using the efficient partial condensing algorithm implemented in HPIPM. We demonstrate the capabilities of our architecture using the Crazyflie 2.1 nano-quadrotor.

On the Promise of the Stochastic Generalized Gauss-Newton Method for Training DNNs

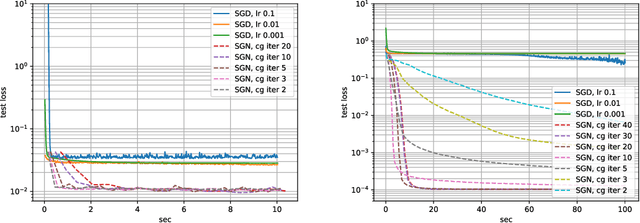
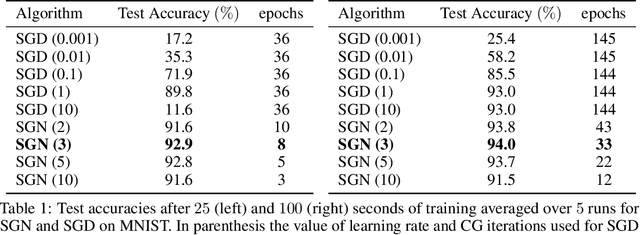
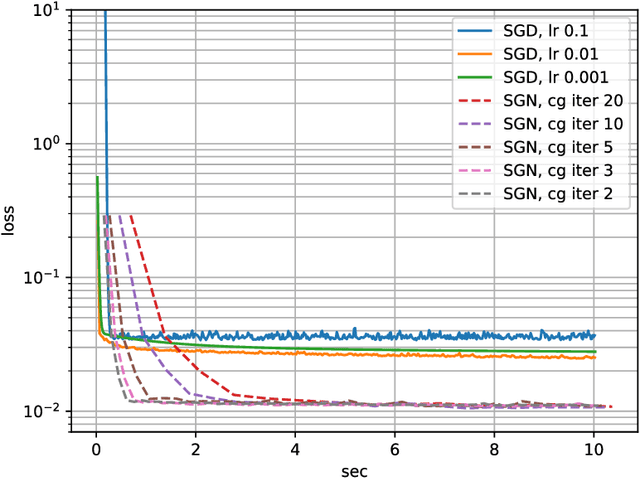
Following early work on Hessian-free methods for deep learning, we study a stochastic generalized Gauss-Newton method (SGN) for training DNNs. SGN is a second-order optimization method, with efficient iterations, that we demonstrate to often require substantially fewer iterations than standard SGD to converge. As the name suggests, SGN uses a Gauss-Newton approximation for the Hessian matrix, and, in order to compute an approximate search direction, relies on the conjugate gradient method combined with forward and reverse automatic differentiation. Despite the success of SGD and its first-order variants, and despite Hessian-free methods based on the Gauss-Newton Hessian approximation having been already theoretically proposed as practical methods for training DNNs, we believe that SGN has a lot of undiscovered and yet not fully displayed potential in big mini-batch scenarios. For this setting, we demonstrate that SGN does not only substantially improve over SGD in terms of the number of iterations, but also in terms of runtime. This is made possible by an efficient, easy-to-use and flexible implementation of SGN we propose in the Theano deep learning platform, which, unlike Tensorflow and Pytorch, supports forward automatic differentiation. This enables researchers to further study and improve this promising optimization technique and hopefully reconsider stochastic second-order methods as competitive optimization techniques for training DNNs; we also hope that the promise of SGN may lead to forward automatic differentiation being added to Tensorflow or Pytorch. Our results also show that in big mini-batch scenarios SGN is more robust than SGD with respect to its hyperparameters (we never had to tune its step-size for our benchmarks!), which eases the expensive process of hyperparameter tuning that is instead crucial for the performance of first-order methods.

CIAO$^\star$: MPC-based Safe Motion Planning in Predictable Dynamic Environments

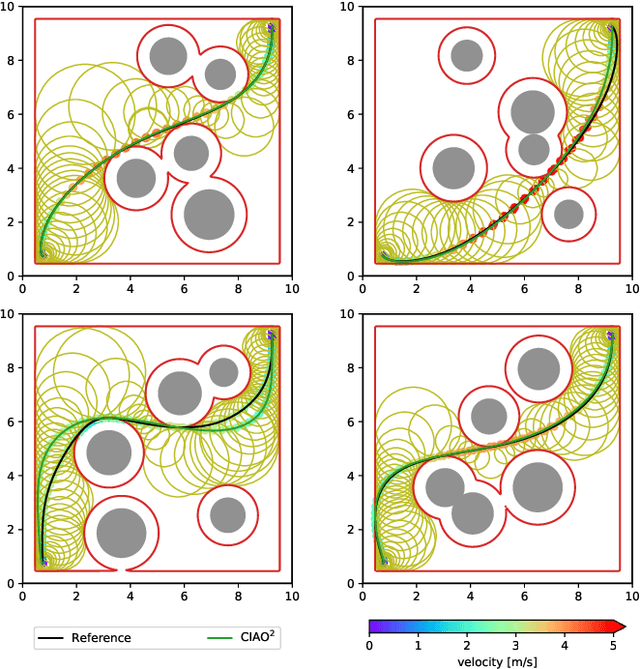
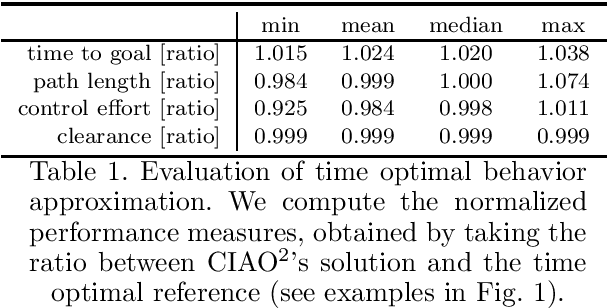
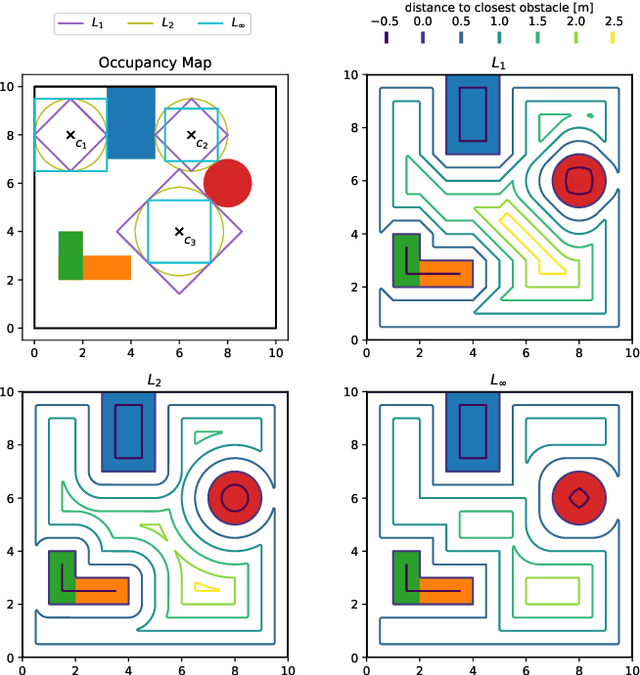
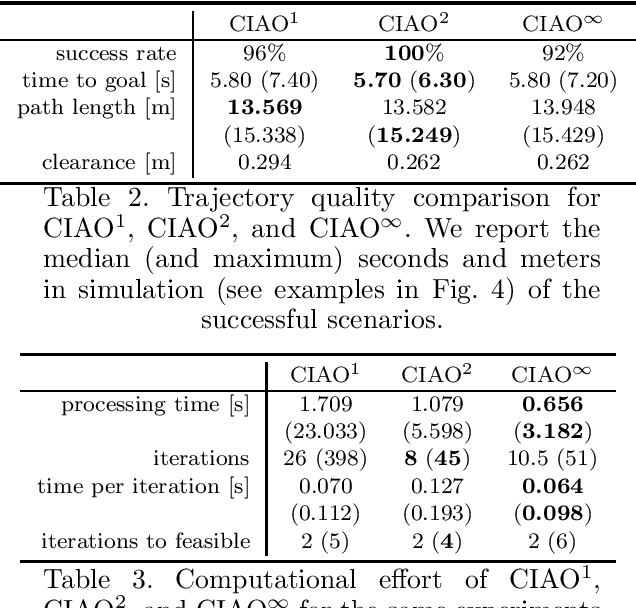
Robots have been operating in dynamic environments and shared workspaces for decades. Most optimization based motion planning methods, however, do not consider the movement of other agents, e.g. humans or other robots, and therefore do not guarantee collision avoidance in such scenarios. This paper builds upon the Convex Inner ApprOximation (CIAO) method and proposes a motion planning algorithm that guarantees collision avoidance in predictable dynamic environments. Furthermore it generalizes CIAO's free region concept to arbitrary norms and proposes a cost function to approximate time-optimal motion planning. The proposed method, CIAO$^\star$, finds kinodynamically feasible and collision free trajectories for constrained robots using a \ac*{mpc} framework and accounts for the predicted movement of other agents. The experimental evaluation shows that CIAO$^\star$ reaches close to time optimal behavior.