Direct Collocation Methods for Trajectory Optimization in Constrained Robotic Systems

Direct collocation methods are powerful tools to solve trajectory optimization problems in robotics. While their resulting trajectories tend to be dynamically accurate, they may also present large kinematic errors in the case of constrained mechanical systems, i.e., those whose state coordinates are subject to holonomic or nonholonomic constraints, like loop-closure or rolling-contact constraints. These constraints confine the robot trajectories to an implicitly-defined manifold, which complicates the computation of accurate solutions. Discretization errors inherent to the transcription of the problem easily make the trajectories drift away from this manifold, which results in physically inconsistent motions that are difficult to track with a controller. This paper reviews existing methods to deal with this problem and proposes new ones to overcome their limitations. Current approaches either disregard the kinematic constraints (which leads to drift accumulation) or modify the system dynamics to keep the trajectory close to the manifold (which adds artificial forces or energy dissipation to the system). The methods we propose, in contrast, achieve full drift elimination on the discrete trajectory, or even along the continuous one, without artificial modifications of the system dynamics. We illustrate and compare the methods using various examples of different complexity.

CIAO$^\star$: MPC-based Safe Motion Planning in Predictable Dynamic Environments

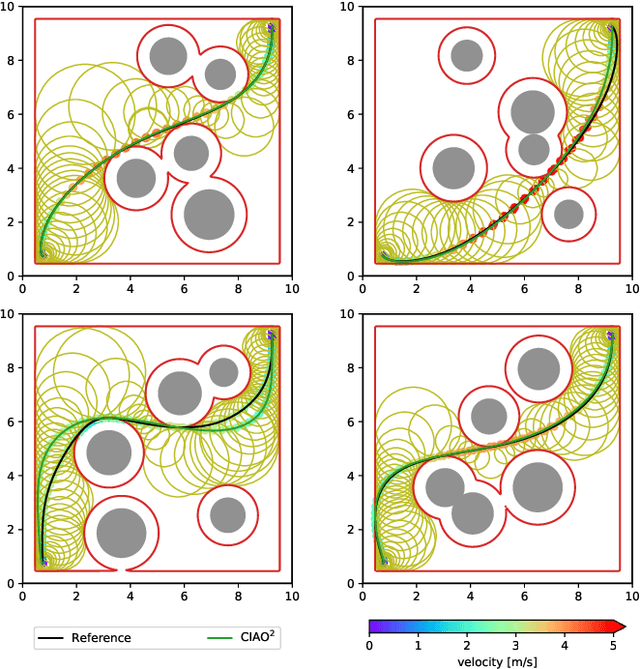
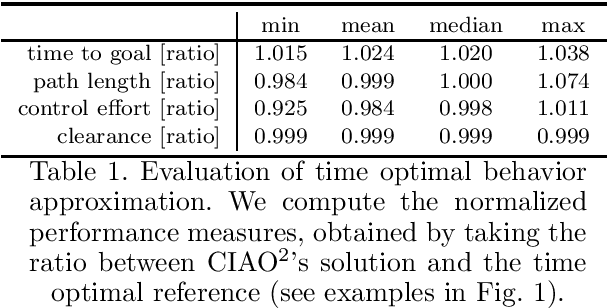
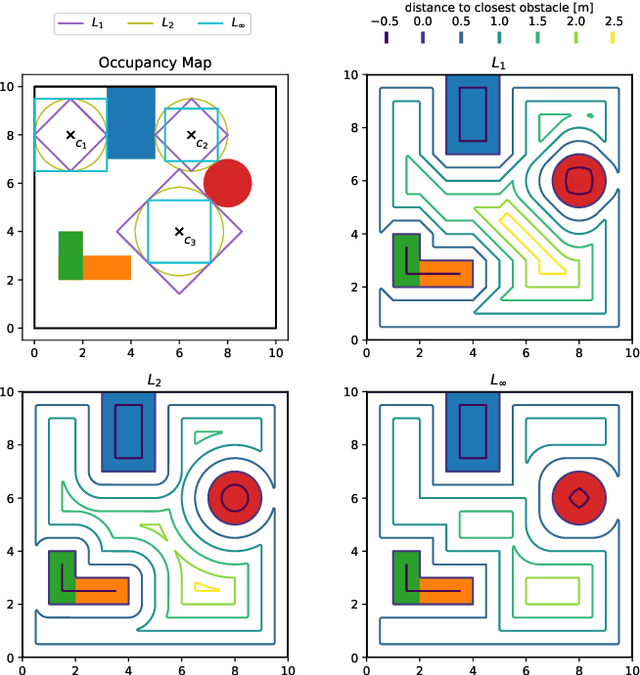
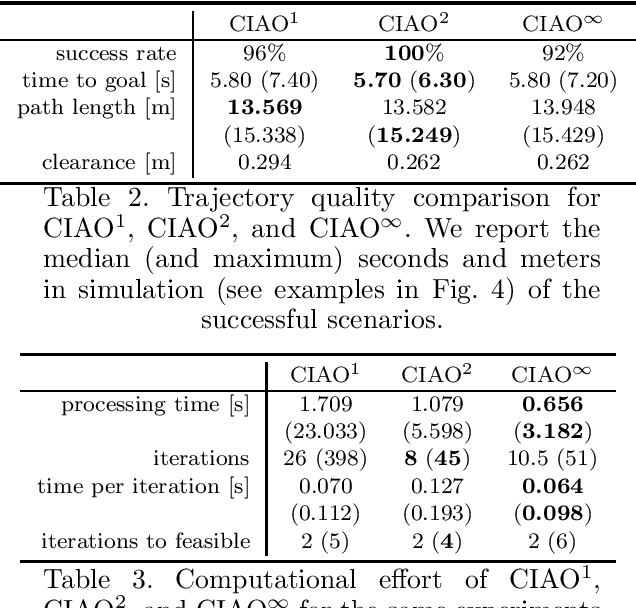
Robots have been operating in dynamic environments and shared workspaces for decades. Most optimization based motion planning methods, however, do not consider the movement of other agents, e.g. humans or other robots, and therefore do not guarantee collision avoidance in such scenarios. This paper builds upon the Convex Inner ApprOximation (CIAO) method and proposes a motion planning algorithm that guarantees collision avoidance in predictable dynamic environments. Furthermore it generalizes CIAO's free region concept to arbitrary norms and proposes a cost function to approximate time-optimal motion planning. The proposed method, CIAO$^\star$, finds kinodynamically feasible and collision free trajectories for constrained robots using a \ac*{mpc} framework and accounts for the predicted movement of other agents. The experimental evaluation shows that CIAO$^\star$ reaches close to time optimal behavior.

An NMPC Approach using Convex Inner Approximations for Online Motion Planning with Guaranteed Collision Freedom

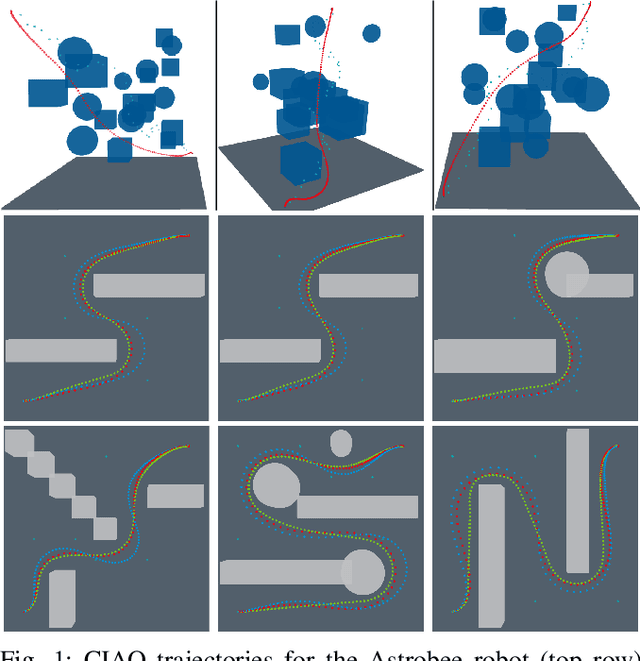
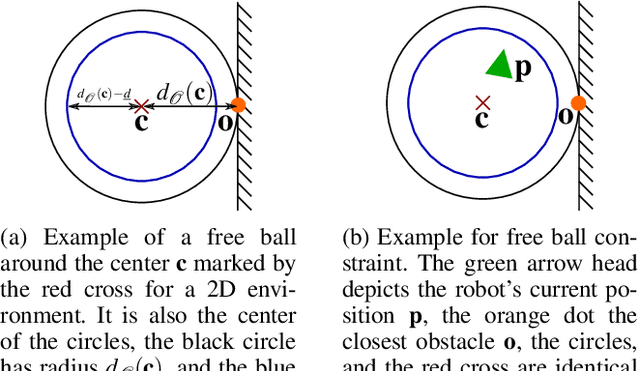
Even though mobile robots have been around for decades, trajectory optimization and continuous time collision avoidance remains subject of active research. Existing methods trade off between path quality, computational complexity, and kinodynamic feasibility. This work approaches the problem using a model predictive control (MPC) framework, that is based on a novel convex inner approximation of the collision avoidance constraint. The proposed Convex Inner ApprOximation (CIAO) method finds a dynamically feasible and collision free trajectory in few iterations, typically one, and preserves feasibility during further iterations. CIAO scales to high-dimensional systems, is computationally efficient, and guarantees both kinodynamic feasibility and continuous-time collision avoidance. Our experimental evaluation shows that the approach outperforms state of the art baselines in terms of planning efficiency and path quality. Furthermore real-world experiments show its capability of unifying trajectory optimization and tracking for safe motion planning in dynamic environments.