CIAO$^\star$: MPC-based Safe Motion Planning in Predictable Dynamic Environments

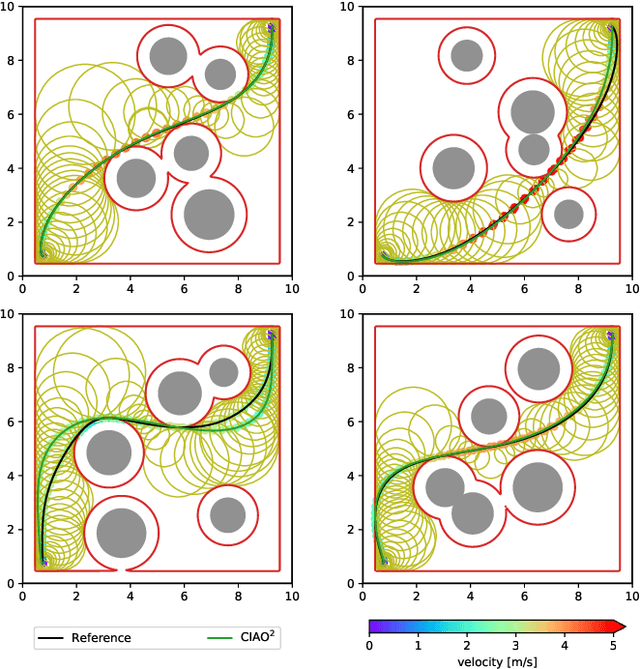
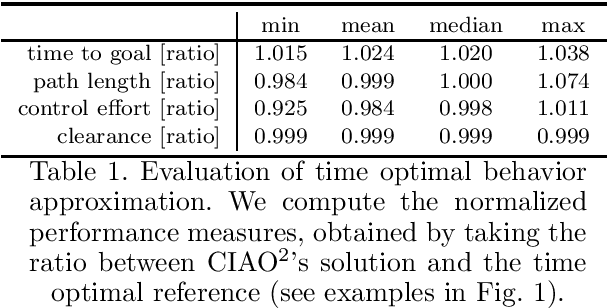
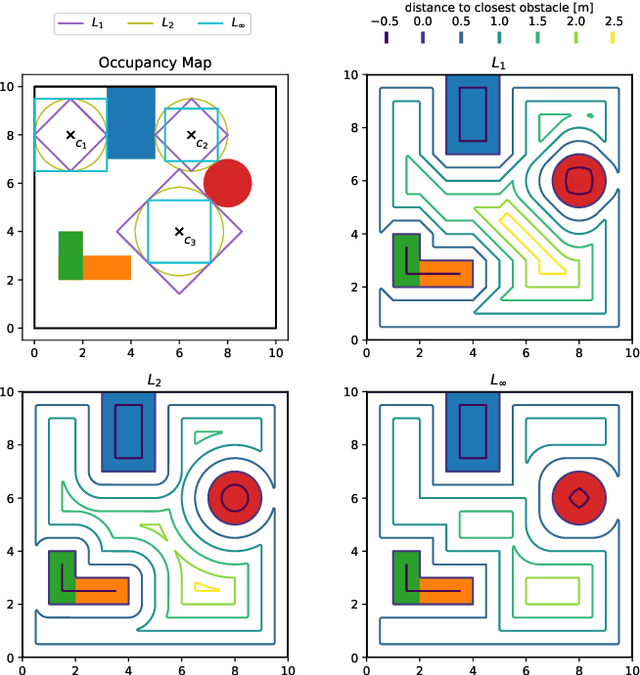
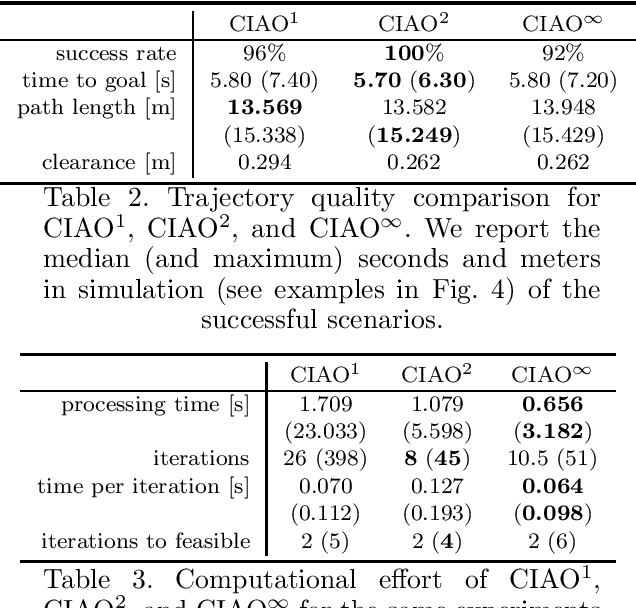
Robots have been operating in dynamic environments and shared workspaces for decades. Most optimization based motion planning methods, however, do not consider the movement of other agents, e.g. humans or other robots, and therefore do not guarantee collision avoidance in such scenarios. This paper builds upon the Convex Inner ApprOximation (CIAO) method and proposes a motion planning algorithm that guarantees collision avoidance in predictable dynamic environments. Furthermore it generalizes CIAO's free region concept to arbitrary norms and proposes a cost function to approximate time-optimal motion planning. The proposed method, CIAO$^\star$, finds kinodynamically feasible and collision free trajectories for constrained robots using a \ac*{mpc} framework and accounts for the predicted movement of other agents. The experimental evaluation shows that CIAO$^\star$ reaches close to time optimal behavior.

Unsupervised Learning through Temporal Smoothing and Entropy Maximization

This paper proposes a method for machine learning from unlabeled data in the form of a time-series. The mapping that is learned is shown to extract slowly evolving information that would be useful for control applications, while efficiently filtering out unwanted, higher-frequency noise. The method consists of training a feedforward artificial neural network with backpropagation using two opposing objectives. The first of these is to minimize the squared changes in activations between time steps of each unit in the network. This "temporal smoothing" has the effect of correlating inputs that occur close in time with outputs that are close in the L2-norm. The second objective is to maximize the log determinant of the covariance matrix of activations in each layer of the network. This objective ensures that information from each layer is passed through to the next. This second objective acts as a balance to the first, which on its own would result in a network with all input weights equal to zero.