Semi-Infinite Programming for Collision-Avoidance in Optimal and Model Predictive Control

This paper presents a novel approach for collision avoidance in optimal and model predictive control, in which the environment is represented by a large number of points and the robot as a union of padded polygons. The conditions that none of the points shall collide with the robot can be written in terms of an infinite number of constraints per obstacle point. We show that the resulting semi-infinite programming (SIP) optimal control problem (OCP) can be efficiently tackled through a combination of two methods: local reduction and an external active-set method. Specifically, this involves iteratively identifying the closest point obstacles, determining the lower-level distance minimizer among all feasible robot shape parameters, and solving the upper-level finitely-constrained subproblems. In addition, this paper addresses robust collision avoidance in the presence of ellipsoidal state uncertainties. Enforcing constraint satisfaction over all possible uncertainty realizations extends the dimension of constraint infiniteness. The infinitely many constraints arising from translational uncertainty are handled by local reduction together with the robot shape parameterization, while rotational uncertainty is addressed via a backoff reformulation. A controller implemented based on the proposed method is demonstrated on a real-world robot running at 20Hz, enabling fast and collision-free navigation in tight spaces. An application to 3D collision avoidance is also demonstrated in simulation.

Differentiable Nonlinear Model Predictive Control

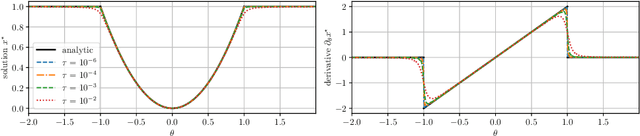
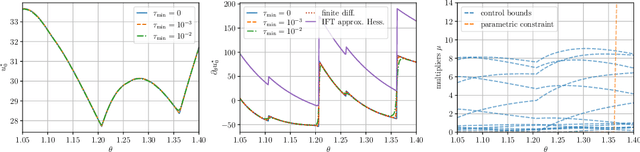
The efficient computation of parametric solution sensitivities is a key challenge in the integration of learning-enhanced methods with nonlinear model predictive control (MPC), as their availability is crucial for many learning algorithms. While approaches presented in the machine learning community are limited to convex or unconstrained formulations, this paper discusses the computation of solution sensitivities of general nonlinear programs (NLPs) using the implicit function theorem (IFT) and smoothed optimality conditions treated in interior-point methods (IPM). We detail sensitivity computation within a sequential quadratic programming (SQP) method which employs an IPM for the quadratic subproblems. The publication is accompanied by an efficient open-source implementation within the framework, providing both forward and adjoint sensitivities for general optimal control problems, achieving speedups exceeding 3x over the state-of-the-art solver mpc.pytorch.

Synthesis of Model Predictive Control and Reinforcement Learning: Survey and Classification

The fields of MPC and RL consider two successful control techniques for Markov decision processes. Both approaches are derived from similar fundamental principles, and both are widely used in practical applications, including robotics, process control, energy systems, and autonomous driving. Despite their similarities, MPC and RL follow distinct paradigms that emerged from diverse communities and different requirements. Various technical discrepancies, particularly the role of an environment model as part of the algorithm, lead to methodologies with nearly complementary advantages. Due to their orthogonal benefits, research interest in combination methods has recently increased significantly, leading to a large and growing set of complex ideas leveraging MPC and RL. This work illuminates the differences, similarities, and fundamentals that allow for different combination algorithms and categorizes existing work accordingly. Particularly, we focus on the versatile actor-critic RL approach as a basis for our categorization and examine how the online optimization approach of MPC can be used to improve the overall closed-loop performance of a policy.

Solgenia -- A Test Vessel Toward Energy-Efficient Autonomous Water Taxi Applications

Autonomous surface vessels are a promising building block of the future's transport sector and are investigated by research groups worldwide. This paper presents a comprehensive and systematic overview of the autonomous research vessel Solgenia including the latest investigations and recently presented methods that contributed to the fields of autonomous systems, applied numerical optimization, nonlinear model predictive control, multi-extended-object-tracking, computer vision, and collision avoidance. These are considered to be the main components of autonomous water taxi applications. Autonomous water taxis have the potential to transform the traffic in cities close to the water into a more efficient, sustainable, and flexible future state. Regarding this transformation, the test platform Solgenia offers an opportunity to gain new insights by investigating novel methods in real-world experiments. An established test platform will strongly reduce the effort required for real-world experiments in the future.

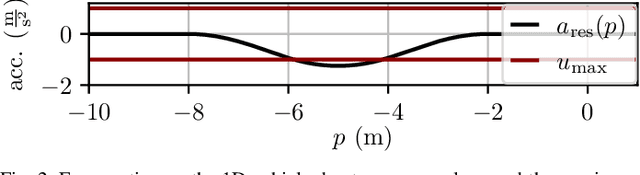
Real-Time-Feasible Collision-Free Motion Planning For Ellipsoidal Objects

Online planning of collision-free trajectories is a fundamental task for robotics and self-driving car applications. This paper revisits collision avoidance between ellipsoidal objects using differentiable constraints. Two ellipsoids do not overlap if and only if the endpoint of the vector between the center points of the ellipsoids does not lie in the interior of the Minkowski sum of the ellipsoids. This condition is formulated using a parametric over-approximation of the Minkowski sum, which can be made tight in any given direction. The resulting collision avoidance constraint is included in an optimal control problem (OCP) and evaluated in comparison to the separating-hyperplane approach. Not only do we observe that the Minkowski-sum formulation is computationally more efficient in our experiments, but also that using pre-determined over-approximation parameters based on warm-start trajectories leads to a very limited increase in suboptimality. This gives rise to a novel real-time scheme for collision-free motion planning with model predictive control (MPC). Both the real-time feasibility and the effectiveness of the constraint formulation are demonstrated in challenging real-world experiments.

Stochastic Model Predictive Control with Optimal Linear Feedback for Mobile Robots in Dynamic Environments

Robot navigation around humans can be a challenging problem since human movements are hard to predict. Stochastic model predictive control (MPC) can account for such uncertainties and approximately bound the probability of a collision to take place. In this paper, to counteract the rapidly growing human motion uncertainty over time, we incorporate state feedback in the stochastic MPC. This allows the robot to more closely track reference trajectories. To this end the feedback policy is left as a degree of freedom in the optimal control problem. The stochastic MPC with feedback is validated in simulation experiments and is compared against nominal MPC and stochastic MPC without feedback. The added computation time can be limited by reducing the number of additional variables for the feedback law with a small compromise in control performance.

AC4MPC: Actor-Critic Reinforcement Learning for Nonlinear Model Predictive Control

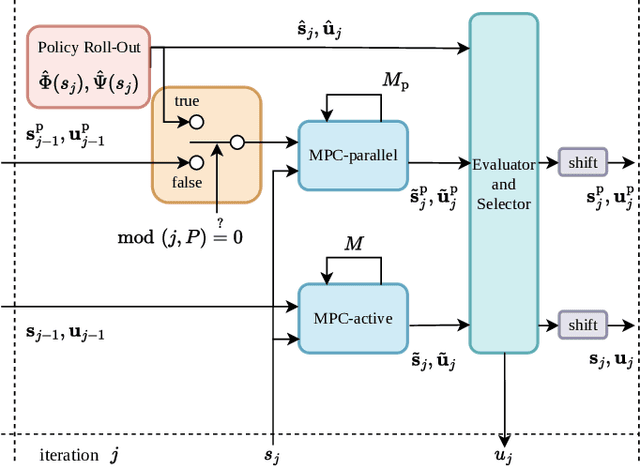
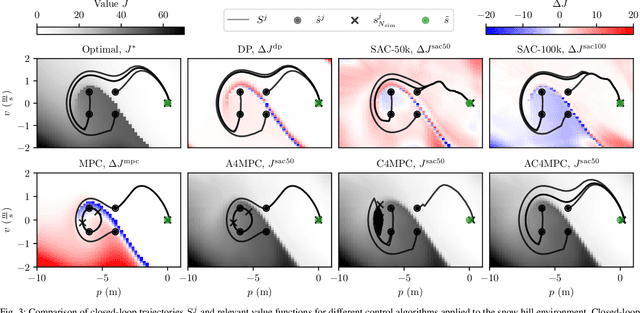
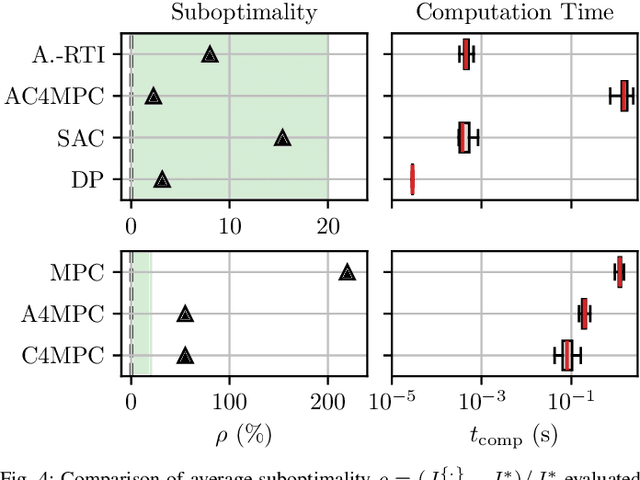
\Ac{MPC} and \ac{RL} are two powerful control strategies with, arguably, complementary advantages. In this work, we show how actor-critic \ac{RL} techniques can be leveraged to improve the performance of \ac{MPC}. The \ac{RL} critic is used as an approximation of the optimal value function, and an actor roll-out provides an initial guess for primal variables of the \ac{MPC}. A parallel control architecture is proposed where each \ac{MPC} instance is solved twice for different initial guesses. Besides the actor roll-out initialization, a shifted initialization from the previous solution is used. Thereafter, the actor and the critic are again used to approximately evaluate the infinite horizon cost of these trajectories. The control actions from the lowest-cost trajectory are applied to the system at each time step. We establish that the proposed algorithm is guaranteed to outperform the original \ac{RL} policy plus an error term that depends on the accuracy of the critic and decays with the horizon length of the \ac{MPC} formulation. Moreover, we do not require globally optimal solutions for these guarantees to hold. The approach is demonstrated on an illustrative toy example and an \ac{AD} overtaking scenario.

Equivariant Deep Learning of Mixed-Integer Optimal Control Solutions for Vehicle Decision Making and Motion Planning

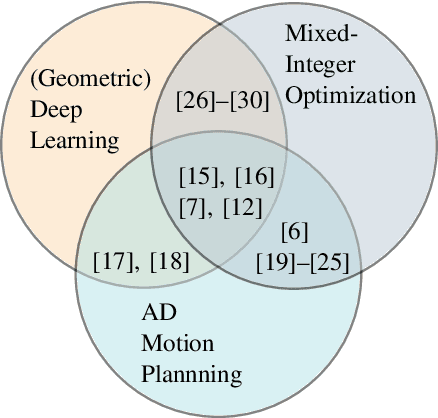
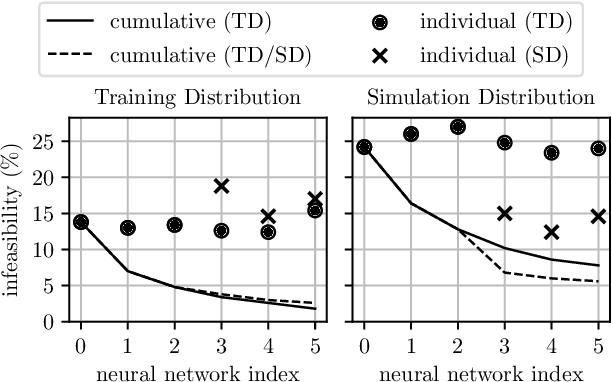
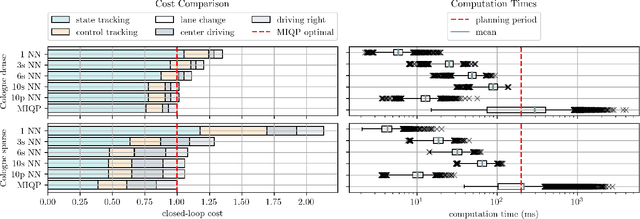
Mixed-integer quadratic programs (MIQPs) are a versatile way of formulating vehicle decision making and motion planning problems, where the prediction model is a hybrid dynamical system that involves both discrete and continuous decision variables. However, even the most advanced MIQP solvers can hardly account for the challenging requirements of automotive embedded platforms. Thus, we use machine learning to simplify and hence speed up optimization. Our work builds on recent ideas for solving MIQPs in real-time by training a neural network to predict the optimal values of integer variables and solving the remaining problem by online quadratic programming. Specifically, we propose a recurrent permutation equivariant deep set that is particularly suited for imitating MIQPs that involve many obstacles, which is often the major source of computational burden in motion planning problems. Our framework comprises also a feasibility projector that corrects infeasible predictions of integer variables and considerably increases the likelihood of computing a collision-free trajectory. We evaluate the performance, safety and real-time feasibility of decision-making for autonomous driving using the proposed approach on realistic multi-lane traffic scenarios with interactive agents in SUMO simulations.

A Long-Short-Term Mixed-Integer Formulation for Highway Lane Change Planning

This work considers the problem of optimal lane changing in a structured multi-agent road environment. A novel motion planning algorithm that can capture long-horizon dependencies as well as short-horizon dynamics is presented. Pivotal to our approach is a geometric approximation of the long-horizon combinatorial transition problem which we formulate in the continuous time-space domain. Moreover, a discrete-time formulation of a short-horizon optimal motion planning problem is formulated and combined with the long-horizon planner. Both individual problems, as well as their combination, are formulated as MIQP and solved in real-time by using state-of-the-art solvers. We show how the presented algorithm outperforms two other state-of-the-art motion planning algorithms in closed-loop performance and computation time in lane changing problems. Evaluations are performed using the traffic simulator SUMO, a custom low-level tracking model predictive controller, and high-fidelity vehicle models and scenarios, provided by the CommonRoad environment.

Direct Collocation Methods for Trajectory Optimization in Constrained Robotic Systems

Direct collocation methods are powerful tools to solve trajectory optimization problems in robotics. While their resulting trajectories tend to be dynamically accurate, they may also present large kinematic errors in the case of constrained mechanical systems, i.e., those whose state coordinates are subject to holonomic or nonholonomic constraints, like loop-closure or rolling-contact constraints. These constraints confine the robot trajectories to an implicitly-defined manifold, which complicates the computation of accurate solutions. Discretization errors inherent to the transcription of the problem easily make the trajectories drift away from this manifold, which results in physically inconsistent motions that are difficult to track with a controller. This paper reviews existing methods to deal with this problem and proposes new ones to overcome their limitations. Current approaches either disregard the kinematic constraints (which leads to drift accumulation) or modify the system dynamics to keep the trajectory close to the manifold (which adds artificial forces or energy dissipation to the system). The methods we propose, in contrast, achieve full drift elimination on the discrete trajectory, or even along the continuous one, without artificial modifications of the system dynamics. We illustrate and compare the methods using various examples of different complexity.