Efficient identification of linear, parameter-varying, and nonlinear systems with noise models

We present a general system identification procedure capable of estimating of a broad spectrum of state-space dynamical models, including linear time-invariant (LTI), linear parameter-varying} (LPV), and nonlinear (NL) dynamics, along with rather general classes of noise models. Similar to the LTI case, we show that for this general class of model structures, including the NL case, the model dynamics can be separated into a deterministic process and a stochastic noise part, allowing to seamlessly tune the complexity of the combined model both in terms of nonlinearity and noise modeling. We parameterize the involved nonlinear functional relations by means of artificial neural-networks (ANNs), although alternative parametric nonlinear mappings can also be used. To estimate the resulting model structures, we optimize a prediction-error-based criterion using an efficient combination of a constrained quasi-Newton approach and automatic differentiation, achieving training times in the order of seconds compared to existing state-of-the-art ANN methods which may require hours for models of similar complexity. We formally establish the consistency guarantees for the proposed approach and demonstrate its superior estimation accuracy and computational efficiency on several benchmark LTI, LPV, and NL system identification problems.

Manifold meta-learning for reduced-complexity neural system identification

System identification has greatly benefited from deep learning techniques, particularly for modeling complex, nonlinear dynamical systems with partially unknown physics where traditional approaches may not be feasible. However, deep learning models often require large datasets and significant computational resources at training and inference due to their high-dimensional parameterizations. To address this challenge, we propose a meta-learning framework that discovers a low-dimensional manifold within the parameter space of an over-parameterized neural network architecture. This manifold is learned from a meta-dataset of input-output sequences generated by a class of related dynamical systems, enabling efficient model training while preserving the network's expressive power for the considered system class. Unlike bilevel meta-learning approaches, our method employs an auxiliary neural network to map datasets directly onto the learned manifold, eliminating the need for costly second-order gradient computations during meta-training and reducing the number of first-order updates required in inference, which could be expensive for large models. We validate our approach on a family of Bouc-Wen oscillators, which is a well-studied nonlinear system identification benchmark. We demonstrate that we are able to learn accurate models even in small-data scenarios.

Exact Gauss-Newton Optimization for Training Deep Neural Networks

We present EGN, a stochastic second-order optimization algorithm that combines the generalized Gauss-Newton (GN) Hessian approximation with low-rank linear algebra to compute the descent direction. Leveraging the Duncan-Guttman matrix identity, the parameter update is obtained by factorizing a matrix which has the size of the mini-batch. This is particularly advantageous for large-scale machine learning problems where the dimension of the neural network parameter vector is several orders of magnitude larger than the batch size. Additionally, we show how improvements such as line search, adaptive regularization, and momentum can be seamlessly added to EGN to further accelerate the algorithm. Moreover, under mild assumptions, we prove that our algorithm converges to an $\epsilon$-stationary point at a linear rate. Finally, our numerical experiments demonstrate that EGN consistently exceeds, or at most matches the generalization performance of well-tuned SGD, Adam, and SGN optimizers across various supervised and reinforcement learning tasks.

A Long-Short-Term Mixed-Integer Formulation for Highway Lane Change Planning

This work considers the problem of optimal lane changing in a structured multi-agent road environment. A novel motion planning algorithm that can capture long-horizon dependencies as well as short-horizon dynamics is presented. Pivotal to our approach is a geometric approximation of the long-horizon combinatorial transition problem which we formulate in the continuous time-space domain. Moreover, a discrete-time formulation of a short-horizon optimal motion planning problem is formulated and combined with the long-horizon planner. Both individual problems, as well as their combination, are formulated as MIQP and solved in real-time by using state-of-the-art solvers. We show how the presented algorithm outperforms two other state-of-the-art motion planning algorithms in closed-loop performance and computation time in lane changing problems. Evaluations are performed using the traffic simulator SUMO, a custom low-level tracking model predictive controller, and high-fidelity vehicle models and scenarios, provided by the CommonRoad environment.

Regularized Gauss-Newton for Optimizing Overparameterized Neural Networks

The generalized Gauss-Newton (GGN) optimization method incorporates curvature estimates into its solution steps, and provides a good approximation to the Newton method for large-scale optimization problems. GGN has been found particularly interesting for practical training of deep neural networks, not only for its impressive convergence speed, but also for its close relation with neural tangent kernel regression, which is central to recent studies that aim to understand the optimization and generalization properties of neural networks. This work studies a GGN method for optimizing a two-layer neural network with explicit regularization. In particular, we consider a class of generalized self-concordant (GSC) functions that provide smooth approximations to commonly-used penalty terms in the objective function of the optimization problem. This approach provides an adaptive learning rate selection technique that requires little to no tuning for optimal performance. We study the convergence of the two-layer neural network, considered to be overparameterized, in the optimization loop of the resulting GGN method for a given scaling of the network parameters. Our numerical experiments highlight specific aspects of GSC regularization that help to improve generalization of the optimized neural network. The code to reproduce the experimental results is available at https://github.com/adeyemiadeoye/ggn-score-nn.

Linear and nonlinear system identification under $\ell_1$- and group-Lasso regularization via L-BFGS-B

In this paper, we propose an approach for identifying linear and nonlinear discrete-time state-space models, possibly under $\ell_1$- and group-Lasso regularization, based on the L-BFGS-B algorithm. For the identification of linear models, we show that, compared to classical linear subspace methods, the approach often provides better results, is much more general in terms of the loss and regularization terms used, and is also more stable from a numerical point of view. The proposed method not only enriches the existing set of linear system identification tools but can be also applied to identifying a very broad class of parametric nonlinear state-space models, including recurrent neural networks. We illustrate the approach on synthetic and experimental datasets and apply it to solve the challenging industrial robot benchmark for nonlinear multi-input/multi-output system identification proposed by Weigand et al. (2022). A Python implementation of the proposed identification method is available in the package \texttt{jax-sysid}, available at \url{https://github.com/bemporad/jax-sysid}.

Self-concordant Smoothing for Convex Composite Optimization

We introduce the notion of self-concordant smoothing for minimizing the sum of two convex functions: the first is smooth and the second may be nonsmooth. Our framework results naturally from the smoothing approximation technique referred to as partial smoothing in which only a part of the nonsmooth function is smoothed. The key highlight of our approach is in a natural property of the resulting problem's structure which provides us with a variable-metric selection method and a step-length selection rule particularly suitable for proximal Newton-type algorithms. In addition, we efficiently handle specific structures promoted by the nonsmooth function, such as $\ell_1$-regularization and group-lasso penalties. We prove local quadratic convergence rates for two resulting algorithms: Prox-N-SCORE, a proximal Newton algorithm and Prox-GGN-SCORE, a proximal generalized Gauss-Newton (GGN) algorithm. The Prox-GGN-SCORE algorithm highlights an important approximation procedure which helps to significantly reduce most of the computational overhead associated with the inverse Hessian. This approximation is essentially useful for overparameterized machine learning models and in the mini-batch settings. Numerical examples on both synthetic and real datasets demonstrate the efficiency of our approach and its superiority over existing approaches.

Global and Preference-based Optimization with Mixed Variables using Piecewise Affine Surrogates

Optimization problems involving mixed variables, i.e., variables of numerical and categorical nature, can be challenging to solve, especially in the presence of complex constraints. Moreover, when the objective function is the result of a simulation or experiment, it may be expensive to evaluate. In this paper, we propose a novel surrogate-based global optimization algorithm, called PWAS, based on constructing a piecewise affine surrogate of the objective function over feasible samples. We introduce two types of exploration functions to efficiently search the feasible domain via mixed integer linear programming (MILP) solvers. We also provide a preference-based version of the algorithm, called PWASp, which can be used when only pairwise comparisons between samples can be acquired while the objective function remains unquantified. PWAS and PWASp are tested on mixed-variable benchmark problems with and without constraints. The results show that, within a small number of acquisitions, PWAS and PWASp can often achieve better or comparable results than other existing methods.

A learning-based approach to multi-agent decision-making

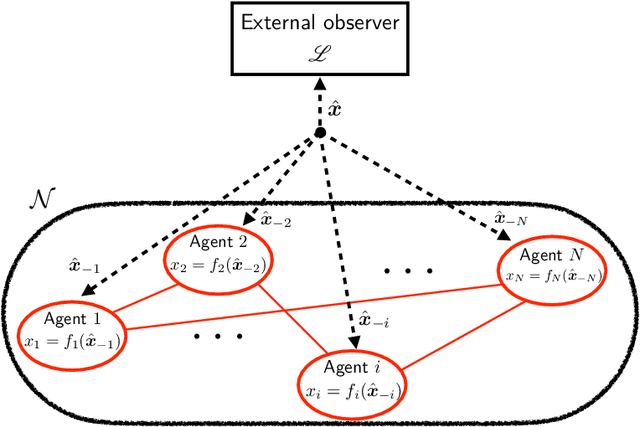
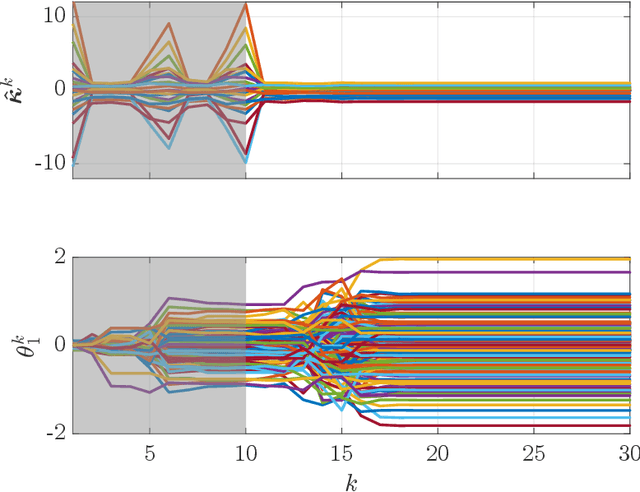
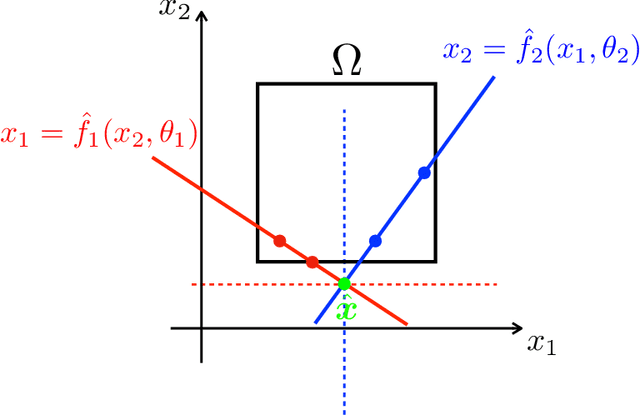
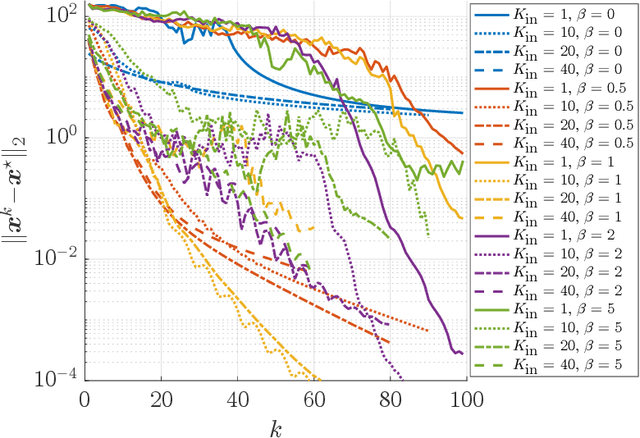
We propose a learning-based methodology to reconstruct private information held by a population of interacting agents in order to predict an exact outcome of the underlying multi-agent interaction process, here identified as a stationary action profile. We envision a scenario where an external observer, endowed with a learning procedure, is allowed to make queries and observe the agents' reactions through private action-reaction mappings, whose collective fixed point corresponds to a stationary profile. By adopting a smart query process to iteratively collect sensible data and update parametric estimates, we establish sufficient conditions to assess the asymptotic properties of the proposed learning-based methodology so that, if convergence happens, it can only be towards a stationary action profile. This fact yields two main consequences: i) learning locally-exact surrogates of the action-reaction mappings allows the external observer to succeed in its prediction task, and ii) working with assumptions so general that a stationary profile is not even guaranteed to exist, the established sufficient conditions hence act also as certificates for the existence of such a desirable profile. Extensive numerical simulations involving typical competitive multi-agent control and decision making problems illustrate the practical effectiveness of the proposed learning-based approach.

Governor: a Reference Generator for Nonlinear Model Predictive Control in Legged Robots

Model Predictive Control (MPC) approaches are widely used in robotics, since they allow to compute updated trajectories while the robot is moving. They generally require heuristic references for the tracking terms and proper tuning of parameters of the cost function in order to obtain good performance. When for example, a legged robot has to react to disturbances from the environment (e.g., recover after a push) or track a certain goal with statically unstable gaits, the effectiveness of the algorithm can degrade. In this work we propose a novel optimization-based Reference Generator, named Governor, which exploits a Linear Inverted Pendulum model to compute reference trajectories for the Center of Mass, while taking into account the possible under-actuation of a gait (e.g. in a trot). The obtained trajectories are used as references for the cost function of the Nonlinear MPC presented in our previous work [1]. We also present a formulation that can guarantee a certain response time to reach a goal, without the need to tune the weights of the cost terms. In addition, foothold locations are corrected to drive the robot towards the goal. We demonstrate the effectiveness of our approach both in simulations and experiments in different scenarios with the Aliengo robot.