Incremental Gauss-Newton Descent for Machine Learning

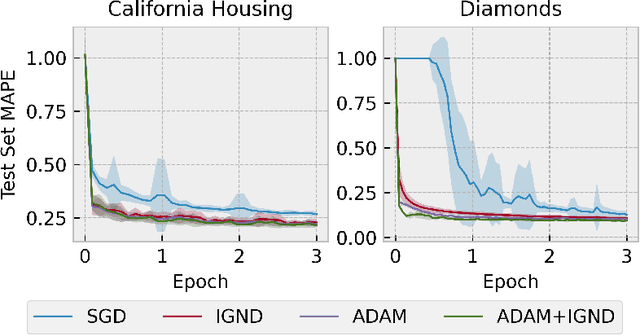
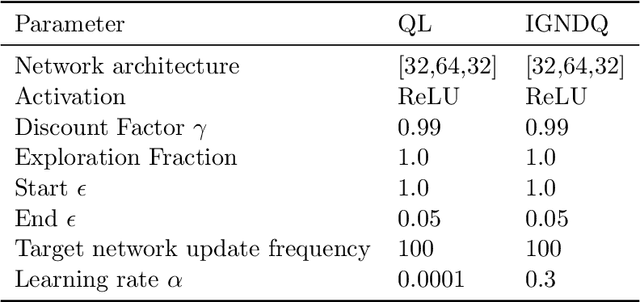
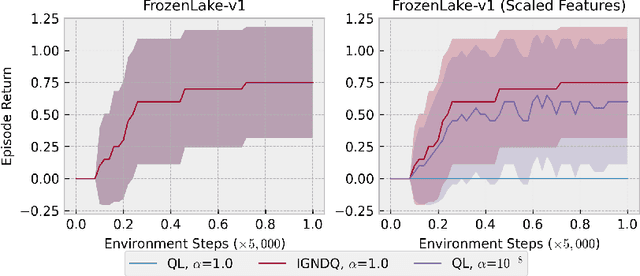
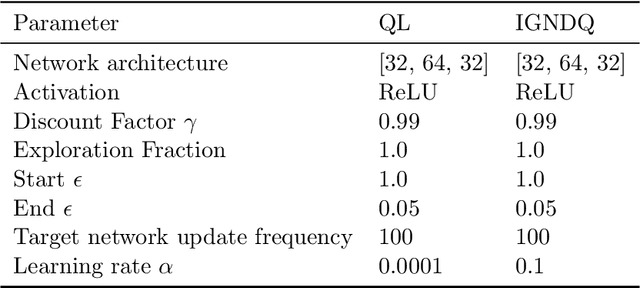
Stochastic Gradient Descent (SGD) is a popular technique used to solve problems arising in machine learning. While very effective, SGD also has some weaknesses and various modifications of the basic algorithm have been proposed in order to at least partially tackle them, mostly yielding accelerated versions of SGD. Filling a gap in the literature, we present a modification of the SGD algorithm exploiting approximate second-order information based on the Gauss-Newton approach. The new method, which we call Incremental Gauss-Newton Descent (IGND), has essentially the same computational burden as standard SGD, appears to converge faster on certain classes of problems, and can also be accelerated. The key intuition making it possible to implement IGND efficiently is that, in the incremental case, approximate second-order information can be condensed into a scalar value that acts as a scaling constant of the update. We derive IGND starting from the theory supporting Gauss-Newton methods in a general setting and then explain how IGND can also be interpreted as a well-scaled version of SGD, which makes tuning the algorithm simpler, and provides increased robustness. Finally, we show how IGND can be used in practice by solving supervised learning tasks as well as reinforcement learning problems. The simulations show that IGND can significantly outperform SGD while performing at least as well as SGD in the worst case.

Exact Gauss-Newton Optimization for Training Deep Neural Networks

We present EGN, a stochastic second-order optimization algorithm that combines the generalized Gauss-Newton (GN) Hessian approximation with low-rank linear algebra to compute the descent direction. Leveraging the Duncan-Guttman matrix identity, the parameter update is obtained by factorizing a matrix which has the size of the mini-batch. This is particularly advantageous for large-scale machine learning problems where the dimension of the neural network parameter vector is several orders of magnitude larger than the batch size. Additionally, we show how improvements such as line search, adaptive regularization, and momentum can be seamlessly added to EGN to further accelerate the algorithm. Moreover, under mild assumptions, we prove that our algorithm converges to an $\epsilon$-stationary point at a linear rate. Finally, our numerical experiments demonstrate that EGN consistently exceeds, or at most matches the generalization performance of well-tuned SGD, Adam, and SGN optimizers across various supervised and reinforcement learning tasks.