Incremental Gauss-Newton Descent for Machine Learning
Paper and Code
Aug 10, 2024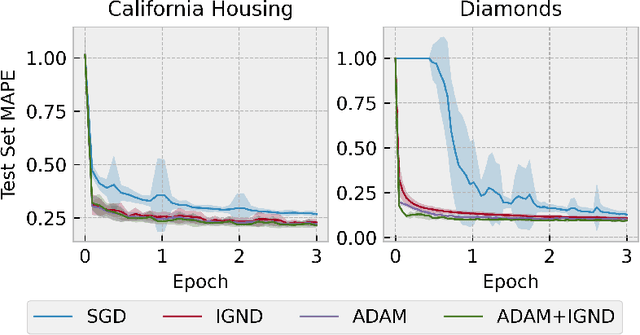
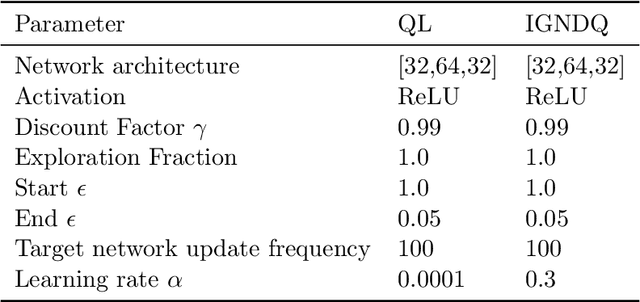
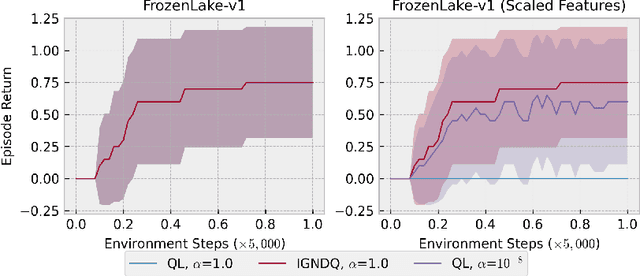
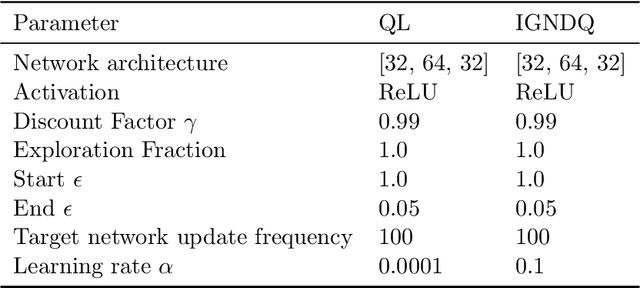
Stochastic Gradient Descent (SGD) is a popular technique used to solve problems arising in machine learning. While very effective, SGD also has some weaknesses and various modifications of the basic algorithm have been proposed in order to at least partially tackle them, mostly yielding accelerated versions of SGD. Filling a gap in the literature, we present a modification of the SGD algorithm exploiting approximate second-order information based on the Gauss-Newton approach. The new method, which we call Incremental Gauss-Newton Descent (IGND), has essentially the same computational burden as standard SGD, appears to converge faster on certain classes of problems, and can also be accelerated. The key intuition making it possible to implement IGND efficiently is that, in the incremental case, approximate second-order information can be condensed into a scalar value that acts as a scaling constant of the update. We derive IGND starting from the theory supporting Gauss-Newton methods in a general setting and then explain how IGND can also be interpreted as a well-scaled version of SGD, which makes tuning the algorithm simpler, and provides increased robustness. Finally, we show how IGND can be used in practice by solving supervised learning tasks as well as reinforcement learning problems. The simulations show that IGND can significantly outperform SGD while performing at least as well as SGD in the worst case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge