Incremental Gauss-Newton Descent for Machine Learning

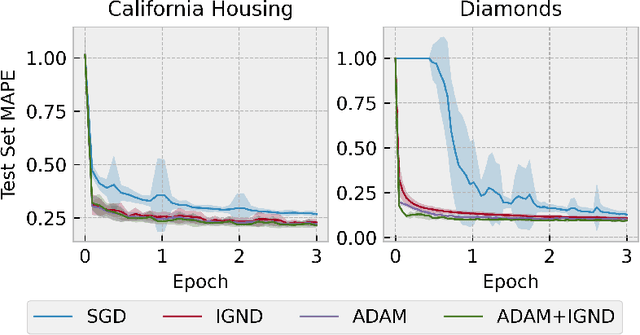
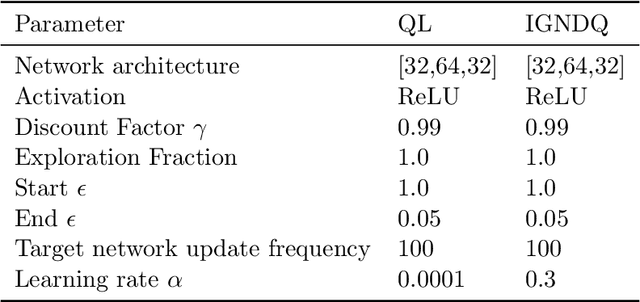
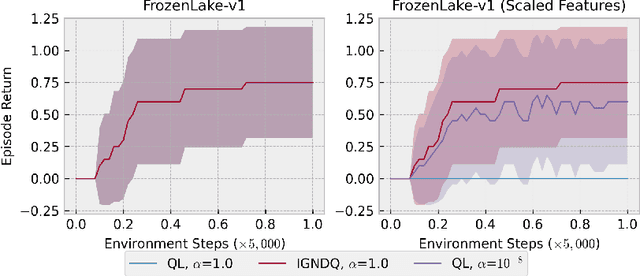
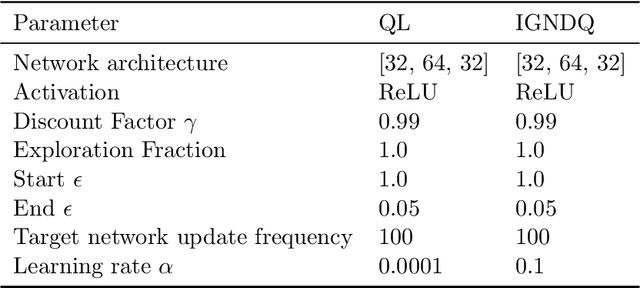
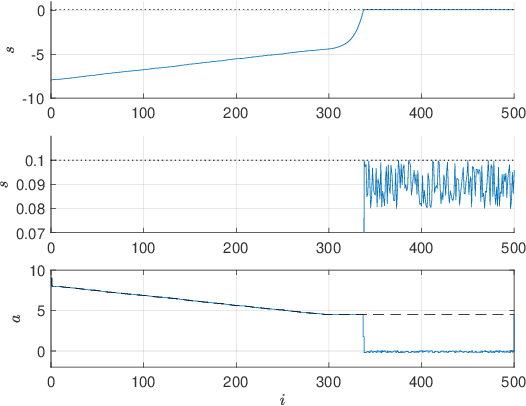
Stochastic Gradient Descent (SGD) is a popular technique used to solve problems arising in machine learning. While very effective, SGD also has some weaknesses and various modifications of the basic algorithm have been proposed in order to at least partially tackle them, mostly yielding accelerated versions of SGD. Filling a gap in the literature, we present a modification of the SGD algorithm exploiting approximate second-order information based on the Gauss-Newton approach. The new method, which we call Incremental Gauss-Newton Descent (IGND), has essentially the same computational burden as standard SGD, appears to converge faster on certain classes of problems, and can also be accelerated. The key intuition making it possible to implement IGND efficiently is that, in the incremental case, approximate second-order information can be condensed into a scalar value that acts as a scaling constant of the update. We derive IGND starting from the theory supporting Gauss-Newton methods in a general setting and then explain how IGND can also be interpreted as a well-scaled version of SGD, which makes tuning the algorithm simpler, and provides increased robustness. Finally, we show how IGND can be used in practice by solving supervised learning tasks as well as reinforcement learning problems. The simulations show that IGND can significantly outperform SGD while performing at least as well as SGD in the worst case.

Exact Gauss-Newton Optimization for Training Deep Neural Networks

We present EGN, a stochastic second-order optimization algorithm that combines the generalized Gauss-Newton (GN) Hessian approximation with low-rank linear algebra to compute the descent direction. Leveraging the Duncan-Guttman matrix identity, the parameter update is obtained by factorizing a matrix which has the size of the mini-batch. This is particularly advantageous for large-scale machine learning problems where the dimension of the neural network parameter vector is several orders of magnitude larger than the batch size. Additionally, we show how improvements such as line search, adaptive regularization, and momentum can be seamlessly added to EGN to further accelerate the algorithm. Moreover, under mild assumptions, we prove that our algorithm converges to an $\epsilon$-stationary point at a linear rate. Finally, our numerical experiments demonstrate that EGN consistently exceeds, or at most matches the generalization performance of well-tuned SGD, Adam, and SGN optimizers across various supervised and reinforcement learning tasks.

Experimental Validation of Safe MPC for Autonomous Driving in Uncertain Environments

The full deployment of autonomous driving systems on a worldwide scale requires that the self-driving vehicle be operated in a provably safe manner, i.e., the vehicle must be able to avoid collisions in any possible traffic situation. In this paper, we propose a framework based on Model Predictive Control (MPC) that endows the self-driving vehicle with the necessary safety guarantees. In particular, our framework ensures constraint satisfaction at all times, while tracking the reference trajectory as close as obstacles allow, resulting in a safe and comfortable driving behavior. To discuss the performance and real-time capability of our framework, we provide first an illustrative simulation example, and then we demonstrate the effectiveness of our framework in experiments with a real test vehicle.

Governor: a Reference Generator for Nonlinear Model Predictive Control in Legged Robots

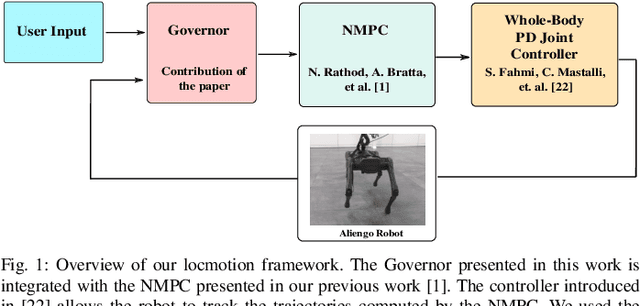
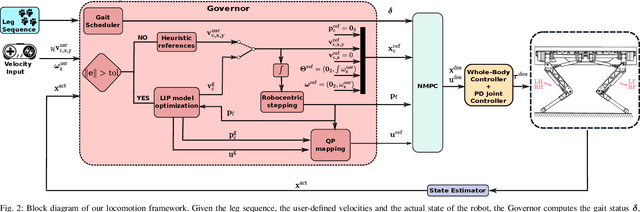
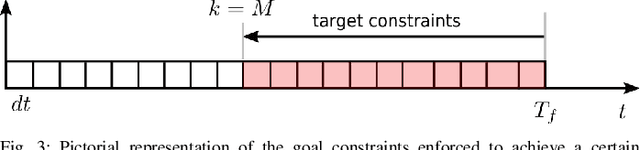
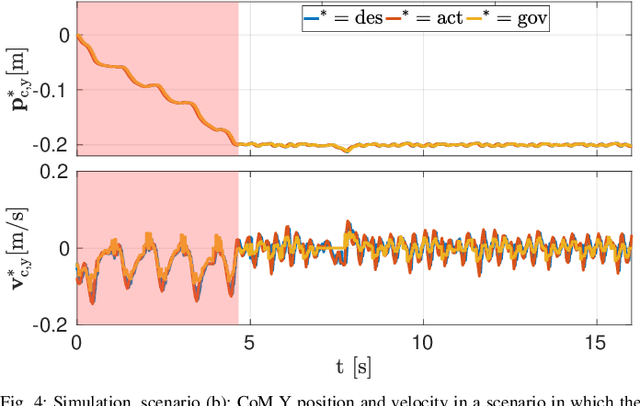
Model Predictive Control (MPC) approaches are widely used in robotics, since they allow to compute updated trajectories while the robot is moving. They generally require heuristic references for the tracking terms and proper tuning of parameters of the cost function in order to obtain good performance. When for example, a legged robot has to react to disturbances from the environment (e.g., recover after a push) or track a certain goal with statically unstable gaits, the effectiveness of the algorithm can degrade. In this work we propose a novel optimization-based Reference Generator, named Governor, which exploits a Linear Inverted Pendulum model to compute reference trajectories for the Center of Mass, while taking into account the possible under-actuation of a gait (e.g. in a trot). The obtained trajectories are used as references for the cost function of the Nonlinear MPC presented in our previous work [1]. We also present a formulation that can guarantee a certain response time to reach a goal, without the need to tune the weights of the cost terms. In addition, foothold locations are corrected to drive the robot towards the goal. We demonstrate the effectiveness of our approach both in simulations and experiments in different scenarios with the Aliengo robot.

Mobility-enhanced MPC for Legged Locomotion on Rough Terrain

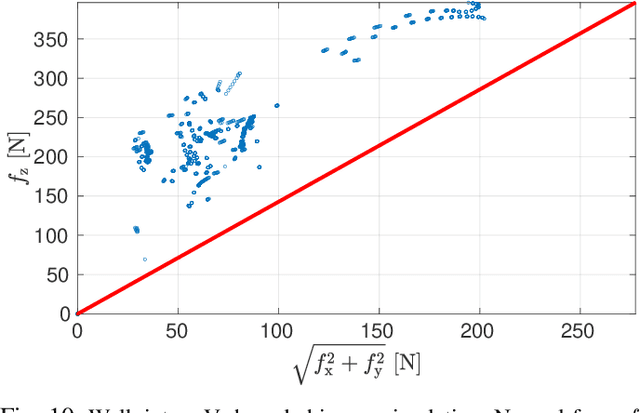
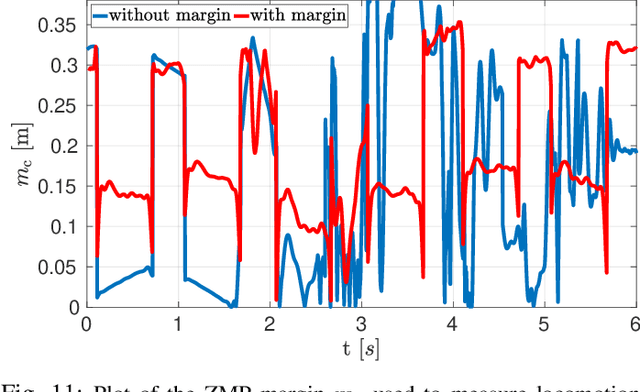
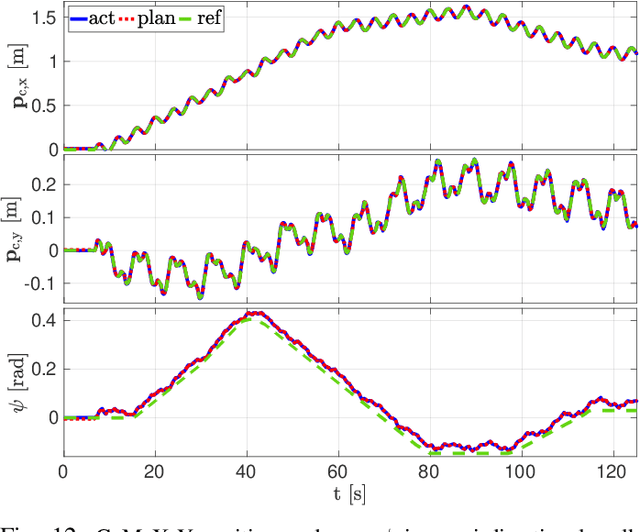
Re-planning in legged locomotion is crucial to track a given set-point while adapting to the terrain and rejecting external disturbances. In this work, we propose a real-time Nonlinear Model Predictive Control (NMPC) tailored to a legged robot for achieving dynamic locomotion on a wide variety of terrains. We introduce a mobility-based criterion to define an NMPC cost that enhances the locomotion of quadruped robots while maximizing leg mobility and staying far from kinematic limits. Our NMPC is based on the real-time iteration scheme that allows us to re-plan online at $25 \, \mathrm{Hz}$ with a time horizon of $2$ seconds. We use the single rigid body dynamic model defined in the center of mass frame that allows to increase the computational efficiency. In simulations, the NMPC is tested to traverse a set of pallets of different sizes, to walk into a V-shaped chimney, and to locomote over rough terrain. We demonstrate the effectiveness of our NMPC with the mobility feature that allowed IIT's $87.4 \,\mathrm{kg}$ quadruped robot HyQ to achieve an omni-directional walk on flat terrain, to traverse a static pallet, and to adapt to a repositioned pallet during a walk in real experiments.

Stability-Constrained Markov Decision Processes Using MPC

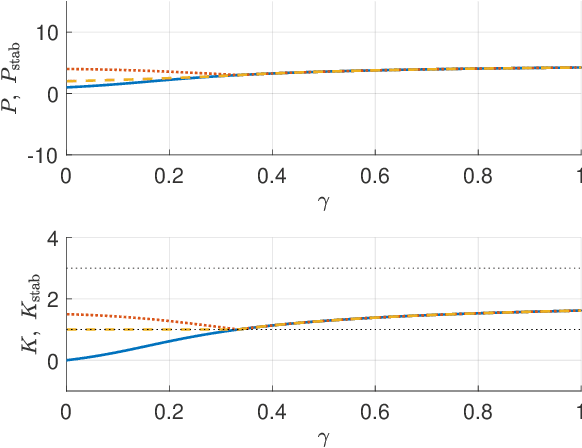
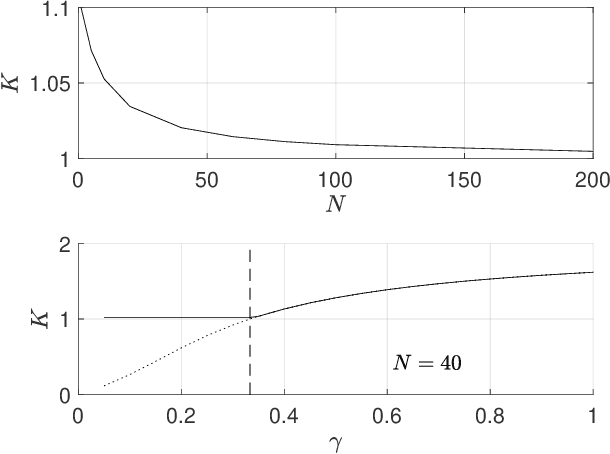
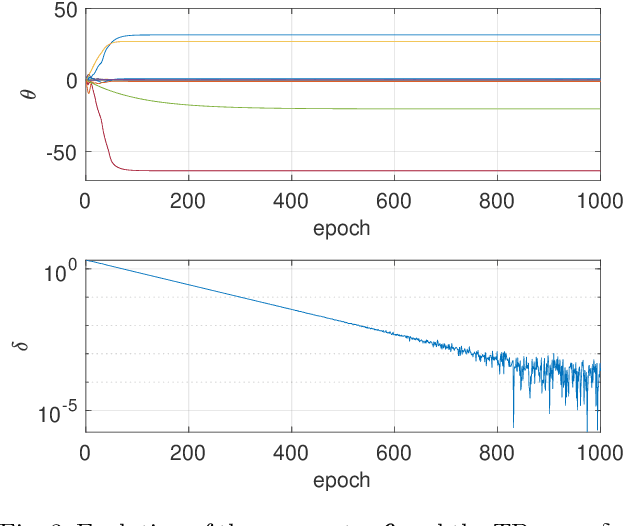
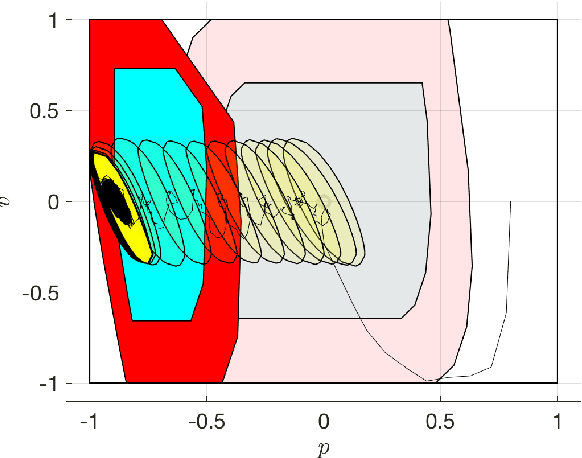
In this paper, we consider solving discounted Markov Decision Processes (MDPs) under the constraint that the resulting policy is stabilizing. In practice MDPs are solved based on some form of policy approximation. We will leverage recent results proposing to use Model Predictive Control (MPC) as a structured policy in the context of Reinforcement Learning to make it possible to introduce stability requirements directly inside the MPC-based policy. This will restrict the solution of the MDP to stabilizing policies by construction. The stability theory for MPC is most mature for the undiscounted MPC case. Hence, we will first show in this paper that stable discounted MDPs can be reformulated as undiscounted ones. This observation will entail that the MPC-based policy with stability requirements will produce the optimal policy for the discounted MDP if it is stable, and the best stabilizing policy otherwise.

Safe Reinforcement Learning with Stability & Safety Guarantees Using Robust MPC

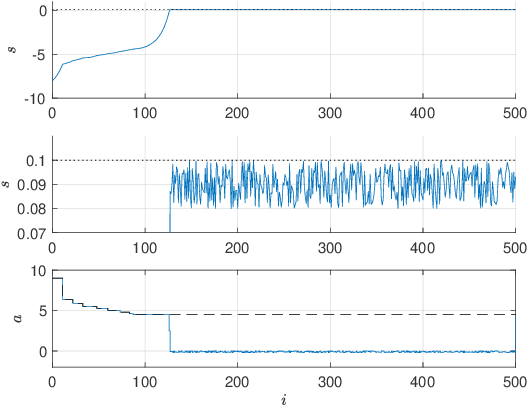
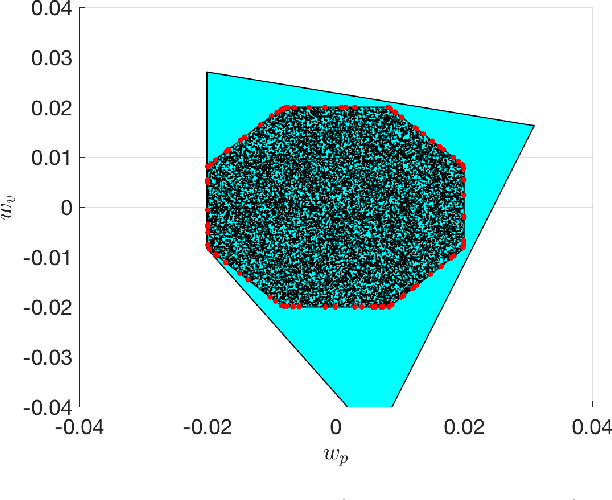
Reinforcement Learning offers tools to optimize policies based on the data obtained from the real system subject to the policy. While the potential of Reinforcement Learning is well understood, many critical aspects still need to be tackled. One crucial aspect is the issue of safety and stability. Recent publications suggest the use of Nonlinear Model Predictive Control techniques in combination with Reinforcement Learning as a viable and theoretically justified approach to tackle these problems. In particular, it has been suggested that robust MPC allows for making formal stability and safety claims in the context of Reinforcement Learning. However, a formal theory detailing how safety and stability can be enforced through the parameter updates delivered by the Reinforcement Learning tools is still lacking. This paper addresses this gap. The theory is developed for the generic robust MPC case, and further detailed in the robust tube-based linear MPC case, where the theory is fairly easy to deploy in practice.

Reinforcement Learning for Mixed-Integer Problems Based on MPC

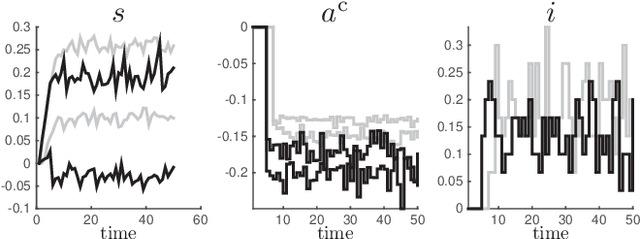
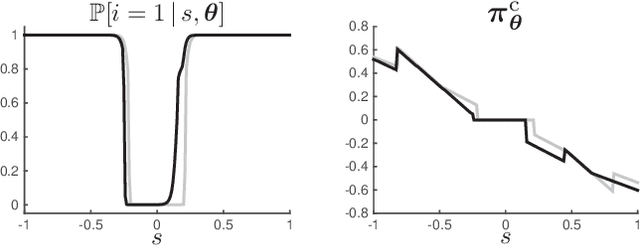
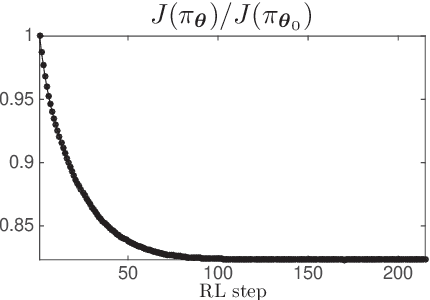
Model Predictive Control has been recently proposed as policy approximation for Reinforcement Learning, offering a path towards safe and explainable Reinforcement Learning. This approach has been investigated for Q-learning and actor-critic methods, both in the context of nominal Economic MPC and Robust (N)MPC, showing very promising results. In that context, actor-critic methods seem to be the most reliable approach. Many applications include a mixture of continuous and integer inputs, for which the classical actor-critic methods need to be adapted. In this paper, we present a policy approximation based on mixed-integer MPC schemes, and propose a computationally inexpensive technique to generate exploration in the mixed-integer input space that ensures a satisfaction of the constraints. We then propose a simple compatible advantage function approximation for the proposed policy, that allows one to build the gradient of the mixed-integer MPC-based policy.

Safe Reinforcement Learning via Projection on a Safe Set: How to Achieve Optimality?

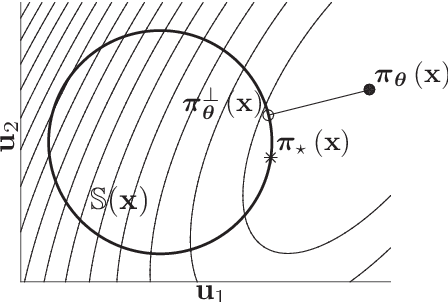
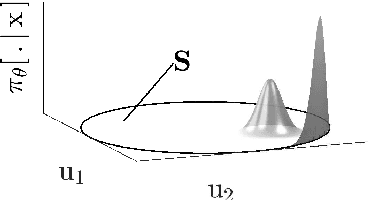
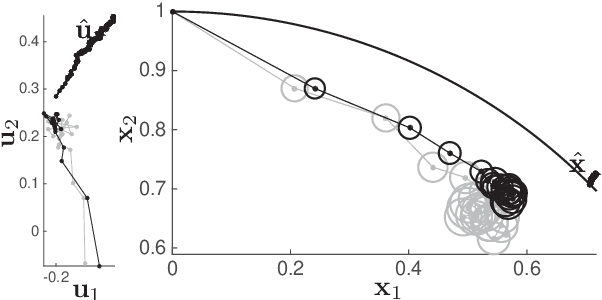
For all its successes, Reinforcement Learning (RL) still struggles to deliver formal guarantees on the closed-loop behavior of the learned policy. Among other things, guaranteeing the safety of RL with respect to safety-critical systems is a very active research topic. Some recent contributions propose to rely on projections of the inputs delivered by the learned policy into a safe set, ensuring that the system safety is never jeopardized. Unfortunately, it is unclear whether this operation can be performed without disrupting the learning process. This paper addresses this issue. The problem is analysed in the context of $Q$-learning and policy gradient techniques. We show that the projection approach is generally disruptive in the context of $Q$-learning though a simple alternative solves the issue, while simple corrections can be used in the context of policy gradient methods in order to ensure that the policy gradients are unbiased. The proposed results extend to safe projections based on robust MPC techniques.