Cost-Matching Model Predictive Control for Efficient Reinforcement Learning in Humanoid Locomotion

In this paper, we propose a cost-matching approach for optimal humanoid locomotion within a Model Predictive Control (MPC)-based Reinforcement Learning (RL) framework. A parameterized MPC formulation with centroidal dynamics is trained to approximate the action-value function obtained from high-fidelity closed-loop data. Specifically, the MPC cost-to-go is evaluated along recorded state-action trajectories, and the parameters are updated to minimize the discrepancy between MPC-predicted values and measured returns. This formulation enables efficient gradient-based learning while avoiding the computational burden of repeatedly solving the MPC problem during training. The proposed method is validated in simulation using a commercial humanoid platform. Results demonstrate improved locomotion performance and robustness to model mismatch and external disturbances compared with manually tuned baselines.

Direct transfer of optimized controllers to similar systems using dimensionless MPC

Scaled model experiments are commonly used in various engineering fields to reduce experimentation costs and overcome constraints associated with full-scale systems. The relevance of such experiments relies on dimensional analysis and the principle of dynamic similarity. However, transferring controllers to full-scale systems often requires additional tuning. In this paper, we propose a method to enable a direct controller transfer using dimensionless model predictive control, tuned automatically for closed-loop performance. With this reformulation, the closed-loop behavior of an optimized controller transfers directly to a new, dynamically similar system. Additionally, the dimensionless formulation allows for the use of data from systems of different scales during parameter optimization. We demonstrate the method on a cartpole swing-up and a car racing problem, applying either reinforcement learning or Bayesian optimization for tuning the controller parameters. Software used to obtain the results in this paper is publicly available at https://github.com/josipkh/dimensionless-mpcrl.

Stability-Constrained Markov Decision Processes Using MPC

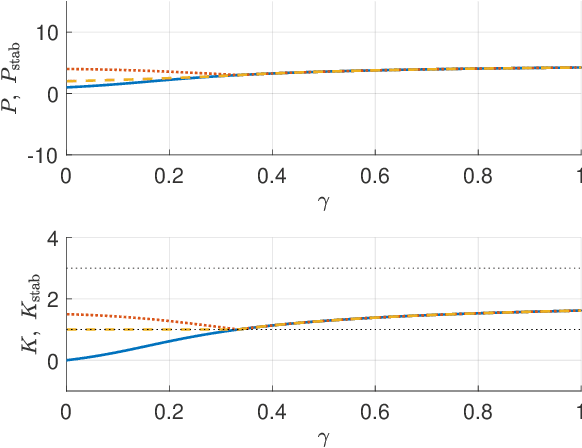
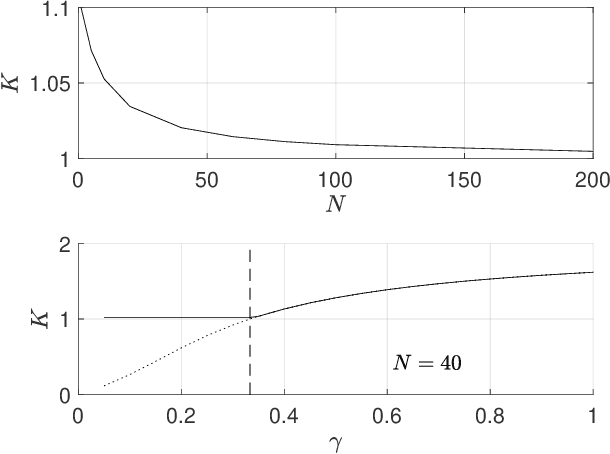
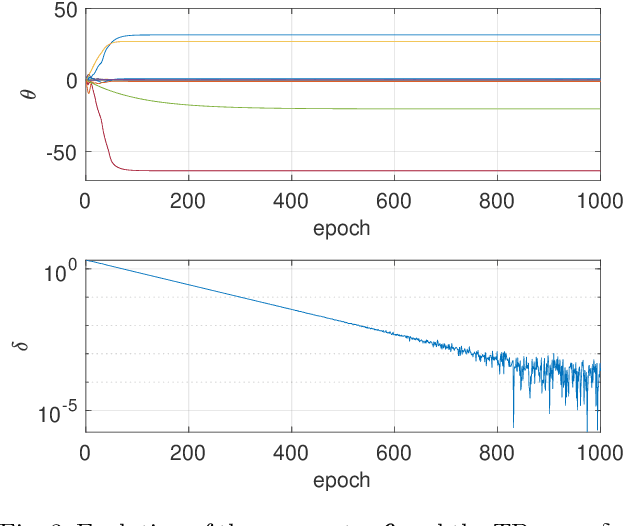
In this paper, we consider solving discounted Markov Decision Processes (MDPs) under the constraint that the resulting policy is stabilizing. In practice MDPs are solved based on some form of policy approximation. We will leverage recent results proposing to use Model Predictive Control (MPC) as a structured policy in the context of Reinforcement Learning to make it possible to introduce stability requirements directly inside the MPC-based policy. This will restrict the solution of the MDP to stabilizing policies by construction. The stability theory for MPC is most mature for the undiscounted MPC case. Hence, we will first show in this paper that stable discounted MDPs can be reformulated as undiscounted ones. This observation will entail that the MPC-based policy with stability requirements will produce the optimal policy for the discounted MDP if it is stable, and the best stabilizing policy otherwise.

Safe Reinforcement Learning with Stability & Safety Guarantees Using Robust MPC

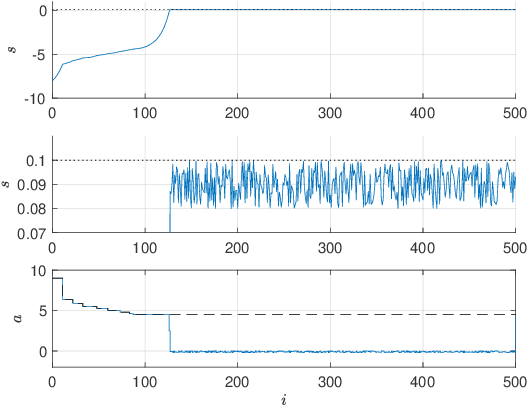
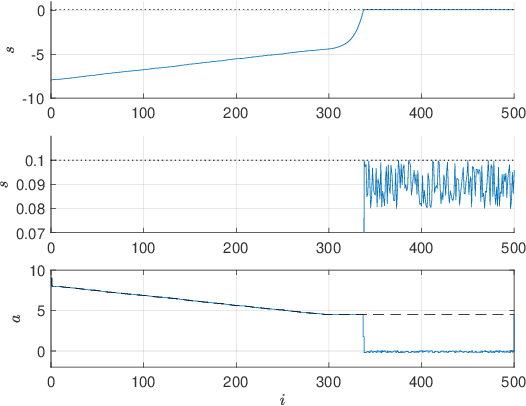
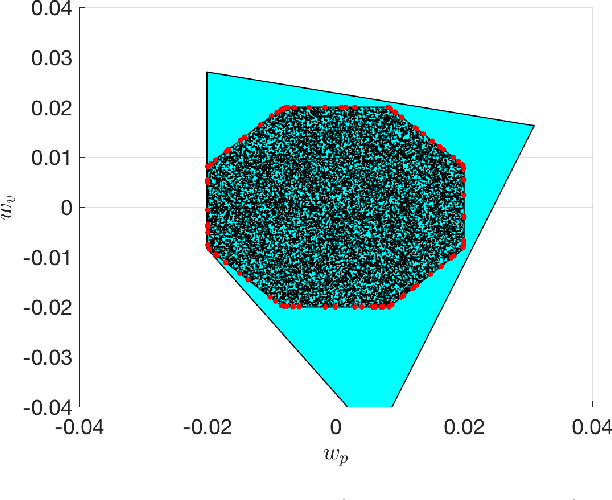
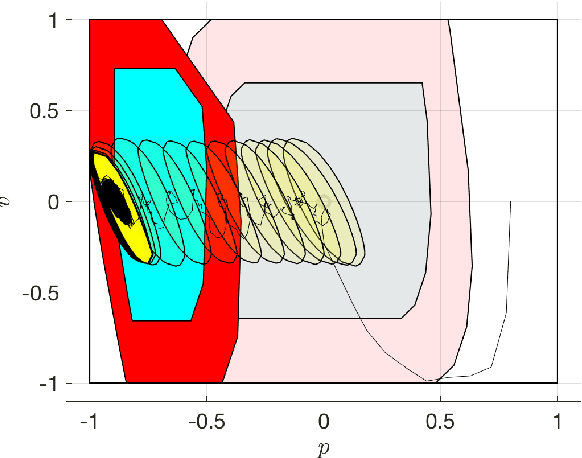
Reinforcement Learning offers tools to optimize policies based on the data obtained from the real system subject to the policy. While the potential of Reinforcement Learning is well understood, many critical aspects still need to be tackled. One crucial aspect is the issue of safety and stability. Recent publications suggest the use of Nonlinear Model Predictive Control techniques in combination with Reinforcement Learning as a viable and theoretically justified approach to tackle these problems. In particular, it has been suggested that robust MPC allows for making formal stability and safety claims in the context of Reinforcement Learning. However, a formal theory detailing how safety and stability can be enforced through the parameter updates delivered by the Reinforcement Learning tools is still lacking. This paper addresses this gap. The theory is developed for the generic robust MPC case, and further detailed in the robust tube-based linear MPC case, where the theory is fairly easy to deploy in practice.